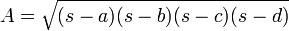Mathématiques indiennes

Contexte des écoles Wikipédia

Arrangeant une sélection Wikipedia pour les écoles dans le monde en développement sans internet était une initiative de SOS Enfants. Cliquez ici pour en savoir plus sur le parrainage d'enfants.

Histoire des sciences

Fond Théories / sociologie Historiographie Pseudoscience
Par époque Dans les premières cultures Dans l'antiquité classique Au Moyen Age A la Renaissance Révolution scientifique Romantisme dans la science
Par la culture Africain Byzantin Chinois Indien Islamique Coréen Mexicain Persan
Sciences naturelles Astronomie Biologie Botanique Chimie Écologie Évolution Géologie Géophysique Paléontologie Physique
Mathématiques Algèbre Calcul Combinatoire Géométrie Logique Probabilité Statistiques Trigonométrie
Sciences sociales Anthropologie Économie Géographie Linguistique Science politique Psychologie Sociologie Durabilité
Technologie La science agricole Informatique La science des matériaux Science militaire
Médecine La médecine alternative Anatomie Anesthésie (général) Biochimie Biotechnologie Cancer Cardiologie (invasive et interventionnelle) Dermatologie Embryologie Endocrinologie Génétique Immunologie Le diagnostic médical Biologie moléculaire Neurologie Neuroscience Nutrition Pathologie Psychiatrie Chirurgie Virologie
Pages de navigation Échéancier Portail Catégories

Mathématiques indiennes -qui Voici les mathématiques qui ont émergé dans Asie du Sud depuis les temps anciens jusqu'à la fin du 18ème siècle, a fait ses débuts dans l' âge du bronze civilisation de l'Indus (2600-1900 BCE) et l' âge du fer Culture védique (1500-500 BCE). Dans la période classique des mathématiques indiennes ( 400 CE pour 1200 CE), d'importantes contributions ont été faites par des savants comme Aryabhatta, Brahmagupta, et Bhaskara II. Mathématiciens indiens ont formulé des premières contributions à l'étude de la système décimal de nombre , de zéro , les nombres négatifs , l'arithmétique et l'algèbre . En outre, la trigonométrie , ayant évolué dans le Monde hellénistique et ayant été introduit dans Inde antique à travers la traduction des grecs œuvres, était plus avancée en Inde, et, en particulier, les définitions modernes de sinus et cosinus y ont été développés. Ces concepts mathématiques ont été transmises au Moyen-Orient , la Chine et l'Europe et a conduit à l'évolution de la qui forment aujourd'hui les fondations de nombreux domaines des mathématiques.

Travaux mathématiques indiennes antiques et médiévaux, tous composés en sanscrit , généralement consisté d'une section de sutras dans lequel un ensemble de règles ou des problèmes ont été formulées avec une grande économie dans le verset afin de faciliter la mémorisation par un étudiant. Elle a été suivie par une seconde section composée d'un commentaire en prose (parfois multiples commentaires par différents chercheurs) qui explique le problème plus en détail et a fourni la justification de la solution. Dans la section de la prose, la forme (et donc sa mémorisation) n'a pas été jugé aussi important que les idées impliquées. Tous les travaux mathématiques ont été transmis oralement jusqu'à environ 500 BCE; par la suite, elles ont été transmises oralement et sous forme de manuscrit. Le plus ancien document mathématique existant produite sur le sous-continent indien est l'écorce de bouleau Bakhshali Manuscrit, découvert en 1881 dans le village de Bakhshali, près de Peshawar (aujourd'hui Pakistan ) et est susceptible de la septième siècle de notre ère.

Un point de repère plus tard en mathématiques indienne a été le développement de la développements en série pour les fonctions trigonométriques (sinus, cosinus, et arc tangente) par les mathématiciens de la Ecole Kerala au XVe siècle de notre ère. Leur travail remarquable, achevée deux siècles avant l'invention de calcul en Europe, à condition ce qui est maintenant considéré comme le premier exemple d'une série de puissance (à l'exception de la série géométrique). Cependant, ils ne ont pas à formuler une théorie systématique de la différenciation et de l'intégration , et il ne existe aucune preuve directe de leurs résultats transmis à l'extérieur Kerala .

Domaines des mathématiques indienne

Certains des domaines des mathématiques étudiés dans l'Inde antique et médiévale sont les suivants:

Arithmétique : Système décimal, nombres négatifs (voir Brahmagupta), Zéro (voir Hindu-Arabe système numérique), le moderne notation positionnelle système de référence numérique , Nombres à virgule flottante (voir Ecole Kerala), théorie des nombres , Infinity (voir Yajur Veda), Nombres transfinis, Les nombres irrationnels (voir Sulba soutras)
Géométrie : Racines carrées (voir Bakhshali approximation), racines cubiques (voir Mahavira), Triplets pythagoriciens (voir Sulba Sutras; Baudhayana et Etat du Apastamba de théorème de Pythagore sans preuve), Transformation (voir Panini), le triangle de Pascal (voir Pingala)
Algèbre : équations du second degré (voir Sulba soutras, Aryabhata, et Brahmagupta), Équations cubiques (voir Mahavira et Bhaskara), Équations quartiques (des équations biquadratiques, voir Mahavira et Bhaskara)
Logique mathématique: Grammaires formelles, théorie des langages formels, le Panini-forme Backus (voir Panini), Recursion (voir Panini)
Mathématiques générales: nombres de Fibonacci (voir Pingala), premières formes de Code Morse (voir Pingala), logarithmes , indices (voir Jaina mathématiques), algorithmes , Algorism (voir Aryabhata et Brahmagupta)
Trigonométrie : fonctions trigonométriques (voir Surya Siddhanta et Aryabhata), Séries trigonométriques (voir Madhava et Ecole Kerala)

Mathématiques indiennes montrent de nombreuses façons différentes de la culture indienne.

Harappan Mathématiques (2600 BCE - 1700 avant notre ère)

La première preuve de l'utilisation des mathématiques dans Asie du Sud est dans les artefacts de la civilisation de l'Indus (IVC), également appelé la civilisation harappéenne. Fouilles à Harappa, Mohenjo Daro (Pakistan) et d'autres endroits dans le fleuve Indus vallée ont découvert des preuves de l'utilisation des mathématiques pratiques. Les habitants de la VCI fabriqués briques dont les dimensions étaient dans la proportion 4: 2: 1, considéré comme favorable à la stabilité d'une structure de briques. Ils ont utilisé un système normalisé de pondérations fondées sur les ratios: 20/01, 10/01, 05/01, 02/01, 1, 2, 5, 10, 20, 50, 100, 200 et 500, à l'unité poids égal à environ 28 grammes (et approximativement égale à la onces anglais ou uncia grec). Ils ont produit de masse poids dans réguliers géométriques formes, qui comprenait hexaèdres, barils, cônes, et cylindres, démontrant ainsi la connaissance de base la géométrie .

Les habitants de la civilisation de l'Indus ont également essayé de normaliser la mesure de la longueur à un haut degré de précision. Ils ont conçu un -dont unité de longueur de la règle-du Mohenjo Daro de la règle (environ 1,32 pouces ou 3,4 cm) a été divisé en dix parties égales. Briques fabriquées dans l'ancienne Mohenjo Daro ont souvent des dimensions qui étaient multiples intégraux de cette unité de longueur.

La tradition orale mathématique

Les mathématiciens de l'ancienne et au début de l'Inde médiévale étaient presque tous sanscrit pandits (PANDITA "savant homme"), qui ont été formés dans la langue et la littérature sanskrite, et possédait "un stock commun de connaissances en grammaire ( Vyakarana), exégèse ( Mimamsa) et logique ( Nyaya). "Mémorisation de" ce qui est entendu "( Sruti en sanskrit) à travers la récitation a joué un rôle majeur dans la transmission des textes sacrés de l'Inde ancienne. Mémorisation et la récitation a également été utilisés pour transmettre des œuvres philosophiques et littéraires, ainsi que des traités sur le rituel et la grammaire. Les savants modernes de l'Inde ancienne ont noté les "réalisations vraiment remarquables des pandits indiens qui ont conservé énormément textes volumineux oralement depuis des millénaires."

Styles de mémorisation

Prodigieuse énergie a été dépensée par la culture indienne ancienne pour se assurer que ces textes ont été transmis de génération en génération avec une fidélité excessive. Par exemple, la mémorisation du sacré Védas inclus jusqu'à onze formes de récitation du même texte. Les textes ont ensuite été "relecture" en comparant les différentes versions citées. Les formes de récitation inclus la JATA-Pathé (littéralement «de la récitation de maille") dans lequel tous les deux mots adjacents dans le texte ont d'abord été récités dans leur ordre original, puis répétées dans l'ordre inverse, et enfin à nouveau répété dans l'ordre original. La récitation a donc procédé comme suit:

word1word2, word2word1, word1word2; word2word3, word3word2, word2word3; ...

Dans une autre forme de récitation, dvaja-Pathé (littéralement «la récitation du pavillon») une séquence de N mots étaient récités (et mémorisé) en associant les deux premiers et les deux derniers mots, puis procéder comme suit:

word1word2, mot (N-1) wordN; word2word3, mot (N-3) mot (N-2); ...; mot (N-1) wordN, word1word2;

La forme la plus complexe de la récitation, le ghana-Pathé (littéralement «récitation dense"), selon (. Filliozat 2004, p 139), a pris la forme:

word1word2, word2word1, word1word2word3, word3word2word1, word1word2word3; word2word3, word3word2, word2word3word4, word4word3word2, word2word3word4; ...

Que ces méthodes ont été efficaces, est témoigné par la préservation de la plus ancienne texte religieux indien, le Rgveda ( ca. 1500 BCE), comme un texte unique, sans lectures variantes. Des procédés similaires ont été utilisés pour mémoriser des textes mathématiques, dont la transmission est resté exclusivement orale jusqu'à la fin de la Période védique (environ 500 avant notre ère).

Le Sutra Genre

L'activité mathématique dans l'Inde ancienne a commencé comme une partie d'une "réflexion méthodologique" sur le sacré Védas, qui a pris la forme de travaux appelé Vedangas, ou «Auxiliaires du Veda» (7e au 4e siècle avant notre ère). La nécessité de conserver le son du texte sacré par l'utilisation de Siksa ( phonétique) et (Chandas métriques); de conserver son sens par l'utilisation de Vyakarana ( grammaire) et Nirukta ( étymologie); et à exécuter correctement les rites au bon moment par l'utilisation de kalpa ( rituel) et jyotiṣa ( astronomie ), a donné lieu à six disciplines de la Vedangas. Mathématiques surgi comme une partie des deux dernières disciplines, le rituel et l'astronomie (qui comprenait également l'astrologie). Depuis le Vedangas immédiatement précédé l'utilisation de l'écriture dans l'Inde ancienne, ils ont formé le dernier de la littérature exclusivement orale. Ils ont été exprimées dans une forme mnémonique hautement compressé, le Sutra (littéralement, "thread"):

Les connaisseurs du Sutra connaissent comme ayant quelques phonèmes, étant dépourvu d'ambiguïté, contenant l'essence, face à tout ce qui, étant sans pause et irréprochable.

Extrême brièveté a été atteint grâce à de multiples moyens, qui comprenaient l'aide points de suspension "au-delà de la tolérance du langage naturel,« en utilisant des noms techniques au lieu des noms plus descriptifs, abrégeant listes que de mentionner les premières et les dernières entrées, et en utilisant des marqueurs et des variables. Les sutras créer l'impression que la communication par le texte était "une partie seulement de l'ensemble instruction. Le reste de l'instruction doit avoir été transmis par la soi-disant Guru-shishya parampara, "succession ininterrompue de maître (guru) à l'étudiant (sisya), 'et ce ne était pas ouvert au grand public secrète" et peut-être même gardé. La brièveté réalisés dans un sutra est démontré dans l'exemple suivant de l'Baudhayana Sulba Sutra (700 BCE).

La conception de l'autel de feu domestique dans le Sûtra Sulba

Le feu-autel domestique dans le Période védique a été requise par le rituel d'avoir une base carrée et être constitué de cinq couches de briques avec 21 briques dans chaque couche. Une méthode de construction de l'autel était de diviser un côté de la place en trois parties égales aide d'un cordon ou de la corde, de diviser ensuite la transversale (ou perpendiculaire) côté en sept parties égales, et ainsi sous-diviser le carré en 21 rectangles congruents . Les briques ont alors été conçus pour être de la forme du rectangle constituant la couche et a été créé. Pour former la couche suivante, la même formule a été utilisée, mais les briques sont disposées transversalement. Le processus a ensuite été répété trois fois (avec les directions alternées) afin de compléter la construction. Dans le Baudhayana Sulba Sûtra, cette procédure est décrite dans les termes suivants:

"II.64. Après divisant le quadri-latéral sur sept, une divise la transversale [cordon] sur trois.
II.65. Dans une autre couche on place le [briques] Nord-pointage. "

Selon (Filliozat 2004, p 144.), Le célébrant la construction de l'autel a seulement quelques outils et matériaux à sa disposition: un cordon (. Sanscrit, rajju, f), deux chevilles (. Sanscrit, Sanku, m), et argile pour faire les briques (sanscrit, iṣṭakā, f.). Concision est réalisé dans le Sutra, en ne mentionnant pas explicitement ce que l'adjectif «transversal» qualifie; Toutefois, à partir de la forme féminine du (sanskrit) adjectif utilisé, il est facile de déduire de se qualifier "cordon". De même, dans la deuxième strophe, «briques» ne sont pas explicitement mentionnés, mais déduits à nouveau par le pluriel féminin de «Nord-pointage." Enfin, la première strophe, dit jamais explicitement que la première couche de briques sont orientées dans le sens Est-Ouest, mais cela aussi est impliquée par la mention explicite du "Nord-pointage" dans la deuxième strophe; car, si l'orientation devait être le même dans les deux couches, il serait soit pas mentionné du tout, ou seulement être mentionné dans la première strophe. Toutes ces déductions sont faites par le célébrant comme il rappelle la formule de sa mémoire.

Période védique (1500 BCE - 400 BCE)

Les textes religieux de la Période védique fournir des preuves de l'utilisation de un grand nombre. Au moment de la dernière Veda, le Yajurvedasaṃhitā (1200-900 BCE), nombres aussi élevés que $10 ^ {12}$ étaient inclus dans les textes. Par exemple, le mantra (formule sacrificielle) à la fin de l'annahoma («nourriture offrande rite") effectuée au cours de la Asvamedha (le «sacrifice du cheval»), et prononcé juste avant-, during-, et juste après le lever du soleil, invoque puissances de dix de cent à un trillion:

"Hail to SATA (" cents " $10 ^ 2$ ), La grêle à sahasra ("mille" $10 ^ 3$ ), La grêle à Ayuta («dix mille», $10 ^ 4$ ), La grêle à niyuta («cent mille», $10 ^ 4$ ), La grêle à prayuta ("millions" $10 ^ 6$ ), La grêle à arbuda ("dix millions" $10 ^ 7$ ), La grêle à nyarbuda ("centaines de millions," $10 ^ 8$ ), La grêle Samudra ("milliards" $10 ^ 9$ , Littéralement «océan»), grêle madhya ("dix milliards," $10 ^ {10}$ , Littéralement «milieu»), grêle anta («centaines de milliards», $10 ^ {11}$ , Allumé, "fin"), la grêle à parardha («un billion," $10 ^ {12}$ allumée, «au-delà des parties"), à l'aube de la grêle (CUA), la grêle au crépuscule (vyuṣṭi), la grêle à celui qui va augmenter (udeṣyat), salut à celui qui est à la hausse (udyat), la grêle à celle qui vient de se lever (udita), la grêle vers le ciel (svarga), la grêle au monde (loka), la grêle à tous ".

Le Satapatha Brahmane (9e siècle avant notre ère) contient des règles pour les constructions géométriques rituelles qui sont semblables aux Sulba Sutras.

Sulba Sûtras

Le Sulba Sûtras (littéralement, "Aphorismes des Accords» dans Sanskrit védique) (c. 700-400 Les règles BCE) de la liste pour la construction des autels de feu sacrificiel. La plupart des problèmes mathématiques considérés au printemps Sulba Sûtras de "une seule exigence théologique," celui de construire des autels du feu qui ont différentes formes, mais occupent la même zone. Les autels ont été nécessaires pour construire de cinq couches de briques cuites, avec la condition supplémentaire que chaque couche composent de 200 briques et qu'aucune deux couches adjacentes ont des arrangements congruentes de briques.

Selon (Hayashi, 2005, p. 363), les sutras Sulba contiennent "l'expression verbale existant plus tôt du théorème de Pythagore dans le monde, même se il avait déjà été appelé à la Old Babyloniens. "

La corde diagonale (akṣṇayā-rajju) d'un oblong (rectangle) qui produit à la fois le flanc (pārśvamāni) et l'horizontale (tiryaṇmānī) produire séparément. "

Depuis la déclaration est un sutra, il est nécessairement comprimé et ce que les cordes produisent ne est pas élaboré, mais le contexte implique clairement les domaines carrés construits sur leurs longueurs, et aurait été expliqué de manière par l'enseignant à l'élève.

Ils contiennent des listes de Triplets pythagoriciens, qui sont des cas particuliers de Équations diophantiennes. Ils contiennent également des déclarations (qui avec le recul que nous savons être approximative) à propos de la quadrature du cercle et «le tour de la place."

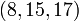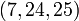Baudhayana (. C 8e siècle avant notre ère) a composé la Baudhayana Sulba Sutra, le plus connu Sutra Sulba, qui contient des exemples de triplets pythagoriciens simples, tels que: $(3, 4, 5)$ , $(5, 12, 13)$ , $(8, 15, 17)$ , $(7, 24, 25)$ Et $(12, 35, 37)$ ainsi qu'un énoncé du théorème de Pythagore pour les côtés d'un carré: «La corde qui se étire à travers la diagonale d'un carré en résulte une zone doubler la taille de la place d'origine." Il contient également l'état général du théorème de Pythagore (pour les côtés d'un rectangle): ". La corde tendue le long de la longueur de la diagonale d'un rectangle présente une surface dont les côtés verticaux et horizontaux forment ensemble" Baudhayana donne une formule pour le racine carrée de deux,

$\ Sqrt {2} = 1 + \ frac {1} {3} + \ frac {1} {3 \ cdot4} - \ frac {1} {3 \ cdot 4 \ cdot 34} \ environ 1,4142156 \ cdots$

La formule est exacte jusqu'à cinq décimales, la valeur réelle $1.41421356 \ cdots$ Cette formule est une structure semblable à la formule trouvée sur une tablette mésopotamienne de la période paléo-babylonienne (1900-1600 BCE):

$\ Sqrt {2} = 1 + \ frac {24} {60} + \ frac {51} {60} ^ 2 + \ frac {10} {60} ^ 3 = 1,41421297.$

qui exprime $\ Sqrt {2}$ dans le système sexagésimal, et qui est trop précise jusqu'à 5 décimales (après arrondissement).

Selon mathématicien SG Dani, la tablette cunéiforme babylonienne Ca. Plimpton 322 écrite 1850 BCE "contient quinze triplets pythagoriciens avec assez grandes entrées, dont 13 500 (12 709,, 18541) qui est un triple primitif, indiquant, en particulier, qu'il y avait connaissance approfondie sur le sujet" en Mésopotamie en 1850 BCE. "Depuis ces comprimés sont antérieurs à la période Sulbasutras par plusieurs siècles, en tenant compte de l'aspect contextuelle de certains des triplets, il est raisonnable de se attendre à ce que la compréhension similaire aurait été là en Inde." Dani poursuit en disant:

"Comme ce était le principal objectif de la Sulvasutras pour décrire les constructions d'autels et les principes géométriques qui y participent, le sujet des triplets pythagoriciens, même si elle avait été bien comprise peut toujours pas avoir présenté dans le Sulvasutras. L'apparition des triplets dans le Sulvasutras est comparable aux mathématiques que l'on peut rencontrer dans un livre d'introduction sur l'architecture ou d'une autre zone d'application similaire, et ne correspondrait pas directement à l'ensemble des connaissances sur le sujet à ce moment-là. Depuis, malheureusement, pas d'autres sources contemporaines ont été trouvés il peut ne jamais être possible de régler cette question de façon satisfaisante ".

Dans les trois Sulba Sutras ont été composées. Les deux autres, le Manava Sulba Sutra composée par Manava (fl. 750-650 BCE) et le Apastamba Sulba Sutra, composée par Apastamba (c. 600 avant notre ère), contenait des résultats similaires à l'Baudhayana Sulba Sutra.

Vyakarana

Une étape importante de la période védique fut l'œuvre de Grammairien sanscrit, Pāṇini (c. 520-460 BCE). Sa grammaire comprend l'utilisation précoce de la logique booléenne , de la opérateur nulle, et grammaires libres de contexte, et comprend un précurseur de la Forme Backus-Naur (utilisés dans la description des langages de programmation ).

Jaina Mathématiques (400 BCE - 200 CE)

Bien que Jaïnisme comme une religion et de la philosophie antérieure à son plus célèbre représentant, Mahavira ( 6ème siècle avant JC), qui était un contemporain de Bouddha Gautama , la plupart des textes de Jaina sur topcs mathématiques ont été composé après la 6e siècle avant notre ère. Jaina mathématiciens sont historiquement important que des liens cruciaux entre les mathématiques de la période védique et celle de la «période classique."

Une contribution historique significative de Jaina mathématiciens réside dans leur libérant les mathématiques indiennes de ses contraintes religieuses et rituelles. En particulier, leur fascination pour l'énumération de très grands nombres et infinis , les conduisit à classer numéros en trois classes: énumérables, innombrables et infinie. Non content d'une simple notion de l'infini, ils sont allés à définir cinq types différents de l'infini: l'infini dans un sens, l'infini dans les deux sens, l'infini dans la zone, l'infini partout, et l'infini perpétuellement. En outre, les mathématiciens Jaina conçus pour des puissances notations simples (et exposants) de nombres comme des carrés et des cubes, ce qui leur a permis de définir simples équations algébriques (beezganit samikaran). Mathématiciens Jaina étaient apparemment aussi le premier à utiliser le mot shunya (littéralement vide dans le sanskrit ) se référer à zéro. Plus d'un millénaire plus tard, leur appellation est devenu le mot anglais "zéro" après un voyage tortueux de traductions et des transcriptions de l'Inde à l'Europe. (Voir zéro: étymologie .)

En plus de Surya Prajnapti important Jaina fonctionne sur les mathématiques comprenaient la Vaishali Ganit (c de BCE 3ème siècle.); l'Sthananga Sutra (fl 300 BCE - 200 CE.); l'Anoyogdwar Sutra (fl 200 BCE - 100 CE.); et l'Satkhandagama (c. de CE 2ème siècle). Mathématiciens Jaina importants inclus Bhadrabahu (d 298 av.), L'auteur de deux ouvrages astronomiques, le Bhadrabahavi-Samhita et un commentaire sur l'Surya Prajinapti; Yativrisham Acharya (c 176 avant notre ère.), Qui a rédigé un texte mathématique appelé Tiloyapannati; et Umasvati (c. 150 BCE), qui, bien que mieux connu pour ses écrits influents sur la philosophie et Jaina la métaphysique, composé une œuvre mathématique appelé Tattwarthadhigama-Sutra Bhashya.

Pingala

Parmi d'autres savants de cette période qui ont contribué à les mathématiques, le plus notable est Pingala (pingala) ( fl. 300-200 BCE), un théoricien de la musique qui a rédigé le Chandas Shastra (chandaḥ-śāstra, également Chandas Sutra chandaḥ-sûtra), un sanscrit traité sur la prosodie. Il est prouvé que dans son ouvrage sur l'énumération des combinaisons syllabiques, Pingala trébuché à la fois du triangle de Pascal et coefficients binomiaux , même se il n'a pas eu connaissance de la Binôme lui-même. Le travail de Pingala contient également les idées de base de nombres de Fibonacci (appelé maatraameru). Bien que le sutra Chandah n'a pas survécu dans son intégralité, un commentaire siècle 10e par Halāyudha a. Halāyudha, qui se réfère à la triangle de Pascal que Meru-prastāra (littéralement "l'escalier Mont Meru "), a ceci à dire:

"Dessinez un carré partir à la moitié de la place, tirer deux autres places similaires dessous;. Dessous de ces deux, trois autres places, et ainsi de suite Le marquage devrait commencer par mettre 1 dans le premier carré Mettez une dans chacun des.. deux places de la deuxième ligne. Dans la troisième ligne mis une dans les deux carrés aux extrémités et, dans le carré du milieu, la somme des chiffres dans les deux carrés situés au-dessus. Dans la quatrième ligne mis une dans les deux places aux extrémités. Au Moyen ceux mis la somme des chiffres dans les deux carrés dessus de chaque. procéder de cette façon. Parmi ces lignes, la seconde donne les combinaisons avec une syllabe, la troisième les combinaisons avec deux syllabes, ... "

Le texte indique également que Pingala était conscient de la combinatoire identité:

${N \ choisissez 0} + {n \ choisissez 1} + {n \ choisir 2} + \ cdots + {n \ choisissent n-1} + {n \ n choisir} = 2 ^ n$

Kâtyâyana

Bien que pas un mathématicien Jaina, Kâtyâyana (c. 3e siècle avant notre ère) est connu pour être le dernier des mathématiciens védiques. Il a écrit le Kâtyâyana Sulba Sutra, qui présentait beaucoup géométrie , y compris le grand théorème de Pythagore et un calcul de la racine carrée de 2 correcte à cinq décimales.

La tradition écrite: Commentaire Prose

Avec la complexité croissante des mathématiques et autres sciences exactes, l'écriture et le calcul ont été tenus. Par conséquent, de nombreux travaux mathématiques ont commencé à être écrit dans les manuscrits qui ont ensuite été copiés et recopiés de génération en génération.

"L'Inde est aujourd'hui estimée à environ trente millions manuscrits, le plus grand corps de matériel de lecture manuscrite ne importe où dans le monde. La culture de l'écrit de la science indienne remonte à au moins le cinquième siècle avant JC ... comme le montrent les éléments de mésopotamienne la littérature et l'astronomie présage qui est entré en Inde à ce moment et (était) certainement pas ... préservés par voie orale. "

Le premier commentaire en prose mathématique, ce est que sur le travail, Aryabhatiya (écrit 499 CE), un travail sur l'astronomie et les mathématiques. La partie mathématique de la Aryabhatiya était composé de 33 sūtras (en forme de vers) constitués de déclarations ou de règles mathématiques, mais sans preuves. Toutefois, selon (Hayashi 2003, p. 123), «cela ne signifie pas nécessairement que leurs auteurs ne ont pas les prouver. Ce est probablement une question de style de l'exposition." A partir du moment de Bhaskara I (600 CE et suivants), commentaires prose plus en plus commencé à inclure des dérivations (upapatti). Le commentaire de Bhaskara I sur la Aryabhatiya, avait la structure suivante:

Règle («soutra») dans le verset par Aryabhata
Commentaire de Bhāskara I, composé de:
- Élucidation des règles (dérivations étaient encore rares alors, mais il est devenu plus fréquent tard)
- Exemple (uddeśaka) généralement en vers.
- Réglage (Nyasa / sthāpanā) des données numériques.
- Travail (Karana) de la solution.
- Vérification (pratyayakaraṇa, littéralement «faire condamnation») de la réponse. Ils sont devenus rares par les 13ème siècle, les dérivations ou des preuves étant favorisé par là.

Typiquement, pour ne importe quel sujet mathématique, les élèves de l'Inde ancienne première mémorisés les sutras, qui, comme expliqué précédemment, étaient «délibérément inadéquate" dans les détails explicatifs (afin de transmettre de manière concise les règles mathématiques nu-os). Les élèves ont ensuite travaillé à travers les thèmes du commentaire en prose par écrit (et dessiner des diagrammes) sur chalk- et de poussière-conseils (c.-conseils couverts de poussière). Cette dernière activité, un aliment de base de travail mathématique, était d'invite tard mathématicien astronome, Brahmagupta ( fl. 7e siècle de notre ère), pour caractériser les calculs astronomiques que "le travail de la poussière" (sanskrit: dhulikarman).

Chiffres et le système de nombre décimal

La plus ancienne existant script utilisé dans l'Inde était le Scénario kharosthî utilisé dans le Gandhara la culture du nord-ouest. On pense que cela soit de Origine araméenne et il était en usage depuis le quatrième siècle avant notre ère au IVe siècle. Presque simultanément, un autre script, le Brahmi, est apparu sur une grande partie du sous-continent, et deviendra plus tard la fondation de nombreux scripts d'Asie du Sud et Asie du Sud-est. Les deux scripts avaient des symboles numériques et systèmes de numération, qui étaient initialement pas fondées sur un système de valeur de. La première preuve datable de l'utilisation du système de valeur de décimale en Inde se trouve dans le Yavanajātaka ( ca. 270 CE) du Sphujidhvaja, une versification d'un plus tôt (environ 150 CE) l'adaptation de la prose indienne d'une œuvre perdue de l'astrologie hellénistique.

Bakhshali Manuscrit

Le plus ancien manuscrit mathématique existant en Asie du Sud est la Bakhshali Manuscrit, un manuscrit de l'écorce de bouleau écrit dans «hybride sanskrit bouddhique" dans le script sarada, qui a été utilisé dans la région nord-ouest du sous-continent indien entre le 8e et 12e siècles de notre ère. Le manuscrit a été découvert en 1881 par un agriculteur en creusant dans une enceinte en pierre dans le village de Bakhshali, près de Peshawar (alors en Inde britannique et maintenant le Pakistan ). L'auteur est inconnu et maintenant conservé dans la Bodleian Library d' Oxford University , le manuscrit a été diversement du-dès les "premiers siècles de l'ère chrétienne" et aussi tard que entre le 9ème et 12ème siècle de notre ère. La CE 7ème siècle est maintenant considéré comme une date plausible, mais avec la probabilité que le "manuscrit dans sa forme actuelle constitue un commentaire ou une copie d'un travail mathématique antérieure."

Le manuscrit survivant a soixante-dix feuilles, dont certaines sont en fragments. Son contenu mathématique comprend des règles et des exemples, écrits en vers, en prose, assortis de commentaires, qui comprennent des solutions aux exemples. Les sujets traités comprennent arithmétiques (fractions, des racines carrées, profits et pertes, l'intérêt simple, les règle de trois, et la fausse position) et l'algèbre (simultanée des équations linéaires et équations du second degré ), et des progressions arithmétiques. En outre, il ya une poignée de problèmes géométriques (y compris les problèmes concernant les volumes de solides irréguliers). Le manuscrit Bakhshali également "utilise un système lieu de valeur décimale avec un point zéro." Beaucoup de ses problèmes sont les problèmes dits péréquation qui conduisent à des systèmes d'équations linéaires. Un exemple de fragment III-5-3v est la suivante:

«Un marchand a sept chevaux de Asava, un deuxième a neuf chevaux de Haya, et un troisième a dix chameaux. Ils sont également bien nantis de la valeur de leurs animaux si chacun donne deux animaux, un pour chacun des autres. Trouver le prix de chaque animal et la valeur totale pour les animaux possédées par chaque marchand ".

Le commentaire en prose accompagnant l'exemple résout le problème en le convertissant en trois (sous-déterminé) équations dans quatre inconnues et en supposant que les prix sont tous les entiers.

Période classique (400 - 1200)

Cette période est souvent connu comme l'âge d'or de mathématiques indiennes. Cette période a vu mathématiciens tels que Aryabhata, Varahamihira, Brahmagupta, Bhaskara I, Mahavira, et Bhaskara II donner une forme plus large et plus claire à de nombreuses branches des mathématiques. Leurs contributions seraient étendre à l'Asie , le Moyen-Orient , et finalement à l'Europe . Contrairement mathématiques védiques, leurs travaux comprenaient deux contributions astronomiques et mathématiques. En fait, les mathématiques de cette période a été inclus dans la «science astrale» (de jyotiḥśāstra) et se composait de trois sous-disciplines: sciences mathématiques (de ganita ou tantra), horoscope astrologie (Hora ou jātaka) et la divination (samhita). Cette division tripartite est vu dans VIe siècle de Varahamihira compilation- Pancasiddhantika (littéralement panca, «cinq», Siddhānta, «conclusion de la délibération", en date du 575 CE) -de cinq œuvres antérieures, Surya Siddhanta, Romaka Siddhanta, Paulisa Siddhanta, Vasishtha Siddhanta et Paitamaha Siddhanta, qui étaient des adaptations d'œuvres encore plus tôt l'astronomie mésopotamienne, grecque, égyptienne, romaine et indienne. Comme expliqué précédemment, les principaux textes ont été composés en sanscrit verset, et ont été suivis par des commentaires en prose.

Ve et VIe siècles

Surya Siddhanta

Bien que son auteur est inconnu, la Surya Siddhanta (c. 400) contient les racines de moderne trigonométrie . Certains auteurs considèrent que sa a été écrit sous l'influence de la Mésopotamie et de la Grèce. Mais selon Flavius Filostratus enregistre Pythagore dans le 5ème siècle avant JC et Apollonius de Tyane au 1er siècle de notre ère est allé étudier dans India.Furthermore n'y a aucune preuve difficile de prouver que les mathématiciens grecs avaient une forte influence sur l'astronomie grecque.

Ce texte ancien utilise ce qui suit comme des fonctions trigonométriques pour la première fois:

Sine (Jya).
Cosinus (Kojya).
Sinus inverse (Otkram de jya).

Il contient également les premières utilisations de:

Tangent .
Secant.

Les cycles de temps cosmologiques hindous expliquées dans le texte, qui a été copié à partir d'un travail antérieur, donne:
- La durée moyenne de la année sidérale que 365.2563627 jours, soit seulement 1,4 secondes de plus que la valeur moderne de 365,2563627 jours.
- La durée moyenne de la année tropicale 365.2421756 jours, ce qui est seulement 2 secondes plus courte que la valeur moderne de 365,2421988 jours.

Plus tard mathématiciens indiens comme Aryabhata faites références à ce texte, tandis que plus tard arabes et latino traductions étaient très influente en Europe et au Moyen-Orient.

Calendrier Chhedi

Ce calendrier Chhedi (594) contient une utilisation précoce de la modernité de valeur de Hindu-Arabe système de numération maintenant utilisé universellement (voir aussi Chiffres indo-arabes).

Je Aryabhata

Aryabhata (476-550) a écrit la Aryabhatiya. Il a décrit les importants principes fondamentaux des mathématiques en 332 shlokas. Le traité contient:

Équations du second degré
Trigonométrie
La valeur de π , correcte à quatre décimales.

Aryabhata a également écrit le Siddhanta Arya, qui est maintenant perdu. Les contributions des Aryabhata comprennent:

Trigonométrie:

Introduit les fonctions trigonométriques .
Défini le sinus (jya) que la relation moderne entre une demi-angle et un demi accord.
Défini le cosinus (kojya).
Définition de la Versine (ukramajya).
Défini le sinus inverse (otkram jya).
Gave méthodes de calcul de leurs valeurs numériques approximatives.
Contient les premiers tableaux de valeurs de sinus, cosinus et Versine, à 3,75 ° intervalles de 0 ° à 90 °, 4 décimales de précision.
Contient le péché trigonométrique formule (n + 1) x - sin nx = sin nx - sin (n - 1) x - (1/225) sin nx.
Trigonométrie sphérique.

Arithmétique:

Fractions continues.

Algèbre:

Solutions d'équations du second degré simultanées.
Solutions de nombre entier d'équations linéairespar une méthode équivalente à la méthode moderne.
Solution générale de l'équation linéaire indéterminée.

L'astronomie mathématique:

Proposé pour la première fois, unhéliocentrique système solaireavec les planètes tournant sur leursaxes et après unelliptiqueorbite autour du Soleil
Des calculs précis pour les constantes astronomiques, comme le:
- Éclipse solaire.
- L'éclipse lunaire.
- La formule pour la somme descubes, ce qui était une étape importante dans le développement du calcul intégral.

Calcul:

Infinitesimals:
- Dans le cadre de l'élaboration d'une cartographie précise de l'éclipse lunaire, Aryabhatta a été obligé d'introduire le concept de infinitésimales (tatkalika gati) pour désigner le mouvement quasi instantanée de la lune.
Équations différentielles:
- Il a exprimé le mouvement quasi instantanée de la lune sous la forme d'une équation différentielle de base.
Fonction exponentielle:
- Il a utilisé lafonction exponentielle edans son équation différentielle du mouvement quasi instantanée de la lune.

Varahamihira

Varahamihira (505-587) a produit le Pancha Siddhanta ( Les Cinq Canons astronomiques ). Il a fait d'importantes contributions à la trigonométrie , y compris les sinus et cosinus tables à 4 décimales de précision et les formules suivantes relatives sinus et cosinus fonctions:

$\sin^2(x) + \cos^2(x) = 1$

$\ Sin (x) = \ cos \ left (\ frac {\ pi} {2} -x \ right)$

$\ frac {1- \ cos (2x)} {2} = \ sin ^ 2 (x)$

Septième et huitième siècles

Le théorème de Brahmagupta stipule que AF = FD.

Au septième siècle, deux domaines distincts, l'arithmétique (qui comprenait mensuration ) et l'algèbre , a commencé à émerger en mathématiques indiennes. Les deux champs qu'on appellera plus tard Pati-ganita (littéralement «les mathématiques d'algorithmes») et BIJA-ganita (littéralement "les mathématiques de graines», avec «graines» -comme les graines de plantes-représentant inconnues avec le potentiel de générer, dans ce cas, les solutions d'équations). Brahmagupta, dans son travail astronomique Brahma Sphuṭa Siddhānta (628 CE), inclus deux chapitres (12 et 18) consacrés à ces domaines. Chapitre 12, contenant 66 versets en sanskrit, a été divisé en deux sections: "les opérations de base" (y compris les racines cubiques, les fractions, rapport et proportions, et de troc) et «mathématiques pratiques» (y compris les mélanges, série mathématique, figures planes, des briques d'empilage, sciage du bois, et l'empilage de céréales). Dans ce dernier article, il a déclaré son célèbre théorème sur les diagonales d'un quadrilatère cyclique:

Le théorème de Brahmagupta: Si un quadrilatère cyclique a diagonales qui sontperpendiculaires l'un à l'autre, alors la ligne perpendiculaire tracée à partir du point d'intersection des diagonales de n'importe quel côté du quadrilatère bissecte toujours du côté opposé.

Chapitre 12 comprend également une formule de l'aire d'un quadrilatère cyclique (une généralisation dela formule de Heron), ainsi qu'une description complète detriangles rationnels (c.-à-triangles dont les côtés sont rationnels et les zones rationnels).

La formule de Brahmagupta:La zone,A, d'unquadrilatère cyclique avec des côtés de longueursde,b,c,d, respectivement, est donnée par

$A = \sqrt{(s-a)(s-b)(s-c)(s-d)}$

oùs, l'semiperimeter, donnée par: $s=\frac{a+b+c+d}{2}.$

Théorème de Brahmagupta sur triangles rationnels:Un triangle dont les côtés rationnels $a, b, c$ et rationnelle zone est de la forme:

$a = \frac{u^2}{v}+v, \ \ b=\frac{u^2}{w}+w, \ \ c=\frac{u^2}{v}+\frac{u^2}{w} - (v+w)$

pour certains nombres rationnels $u, v,$ et $w$ .

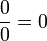Chapitre 18 contenait 103 versets en sanskrit qui a commencé avec les règles pour les opérations arithmétiques impliquant zéro et les nombres négatifs et est considéré comme le premier traitement systématique du sujet. Les règles (qui inclus $a + 0 = \ a$ et $a \times 0 = 0$ ) étaient tous corrects, à une exception près: $\frac{0}{0} = 0$ . plus tard dans le chapitre, il a donné la première solution explicite (bien que pas encore tout à fait général) de l' équation quadratique :

$\ ax^2+bx=c$

Pour le nombre absolu multiplié par quatre fois la [coefficient de la] place, ajouter le carré de la [coefficient de la] à moyen terme; la racine carrée de la même, moins le [coefficient de la] à moyen terme, étant divisée par deux fois le [coefficient de la] carré est la valeur. ( Brahmasphutasiddhanta (traduction Colebrook, 1817, Page 346)

Ceci est équivalent à:

$x = \frac{\sqrt{4ac+b^2}-b}{2a}$

Aussi dans le chapitre 18, Brahmagupta était en mesure de faire des progrès dans la recherche de solutions (intégrale) de l'équation de Pell,

$\ x^2-Ny^2=1,$

où $N$ est un nombre entier non carrés. Il l'a fait en découvrant l'identité suivante:

Brahmagupta de l'identité: $\ (x^2-Ny^2)(x'^2-Ny'^2) = (xx'+Nyy')^2 - N(xy'+x'y)^2$ qui était une généralisation d'une identité antérieure deDiophante: Brahmagupta utilisé son identité pour prouver le lemme suivant:

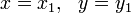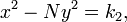Lemme (Brahmagupta):Si $x=x_1,\ \ y=y_1 \ \$ est une solution de $\ \ x^2 - Ny^2 = k_1,$ et, $x=x_2, \ \ y=y_2 \ \$ est une solution de $\ \ x^2 - Ny^2 = k_2,$ , puis:

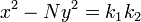
$x=x_1x_2+Ny_1y_2,\ \ y=x_1y_2+x_2y_1 \ \$ est une solution de $\ x^2-Ny^2=k_1k_2$

Il a ensuite utilisé ce lemme à la fois de générer une infinité de solutions (intégrale) de l'équation de Pell, étant donné qu'une solution, et énoncer le théorème suivant:

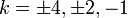Théorème (Brahmagupta):Si l'équation $\ x^2 - Ny^2 =k$ a une solution entière pour une quelconque $\ k=\pm 4, \pm 2, -1$ puis équation de Pell:

$\ x^2 -Ny^2 = 1$

possède également une solution entière.

Brahmagupta n'a pas réellement prouver le théorème, mais plutôt travaillé sur des exemples utilisant sa méthode. Le premier exemple, il a présenté était:

Exemple (Brahmagupta):Trouver entiers $\ x,\ y\$ tel que:

$\ x^2 - 92y^2=1$

Dans son commentaire, Brahmagupta ajouté, "une personne de résoudre ce problème dans un an est un mathématicien." La solution qu'il était prévu:

$\ x=1151, \ y=120$

Je Bhaskara

Bhaskara I (c. 600-680) a élargi le travail de Aryabhata dans ses livres intitulés Mahabhaskariya , Aryabhattiya Bhashya et Laghu Bhaskariya . Il a produit:

Solutions d'équations indéterminées.
Une approximation rationnelle de lafonction sinus.
Une formule pour calculer le sinus d'un angle aigu sans l'utilisation d'une table, de rectification à 2 décimales.

Neuvième à douzième siècles

Virasena

Virasena (9e siècle) était un mathématicien Jaina dans la cour du roi Rashtrakuta Amoghavarsha de Manyakheta, Karnataka. Il a écrit le Dhavala , un commentaire sur les mathématiques Jaina, qui:

Offres avec logarithmes à la base 2 (ardhaccheda) et décrit ses lois.
Première utilise logarithmes de fonder 3 (trakacheda) et la base 4 (caturthacheda).

Virasena également donné:

La dérivation de lavolumiqued'untronc de cône par une sorte de procédure infini.

Mahavira

Mahavira Acharya (c. 800-870) de Karnataka, le dernier des mathématiciens Jaina notables, vivait dans le 9ème siècle et a été patronné par le roi Rashtrakuta Amoghavarsha. Il a écrit un livre intitulé Ganit Sarre Sangraha sur les mathématiques numériques, et a également écrit des traités sur un large éventail de sujets mathématiques. Ceux-ci comprennent les mathématiques de:

Zéro.
Squares.
Cubes.
racines carrées,racines cubiques, et lesséries dépassant ceux-ci.
géométrie plane.
Géométrie solide.
Les problèmes liés à la coulée del'ombre.
Formules dérivé pour calculer l'aire d'uneellipseetl'intérieur d'un quadrilatèrecercle

Mahavira aussi:

A affirmé que laracine carréed'unnombre négatifn'a pas existé
A donné la somme d'unesérie dont les termes sontdes carrés d'uneprogression arithmétique, et a donné des règles empiriques pourla zoneet depérimètre d'uneellipse.
Équations cubiques résolu.
Équations quartiques résolu.
Résolu certaineséquations quintiques et d'ordre supérieurpolynômes.
Gave les solutions générales des équations polynomiales d'ordre supérieur:
- $\ ax^n = q$
- $a \frac{x^n - 1}{x - 1} = p$
Équations du second degré indéterminées résolu.
Équations cubiques indéterminées résolu.
Résolu indéterminées équations d'ordre supérieur.

Shridhara

Shridhara (c. 870-930), qui a vécu dans le Bengale, a écrit les livres intitulés Nav Shatika , Tri Shatika et Pati Ganita . Il a donné:

Une bonne règle pour trouver levolume ded'unesphère.
La formule pour résoudredes équations du second degré.

Le Pati Ganita est un travail sur l'arithmétique et la mensuration . Il traite de diverses opérations, y compris:

Opérations élémentaires
Extraction de racines carrées et cubiques.
Les fractions.
Huit règles données pour les opérations impliquant zéro.
Méthodes desommation de l'arithmétique différent et série géométrique, qui devait devenir références standard dans les œuvres ultérieures.

Manjula

Les équations différentielles de Aryabhata ont été élaborés dans le 10ème siècle par Manjula (égalementMunjala), qui a réalisé que l'expression

$\ \sin w' - \sin w$

peut être exprimée approximativement comme

$\ (w' - w)\cos w$

Il a compris le concept de différenciation après la résolution de l'équation différentielle qui a résulté de la substitution de cette expression dans l'équation différentielle de Aryabhata.

Aryabhata II

Aryabhata II (c. 920 à 1000) a écrit un commentaire sur Shridhara, et un traité d'astronomie Maha-Siddhanta . Le Maha-Siddhanta a 18 chapitres, et discute:

Mathématiques numériques (Ank Ganit).
Algebra.
Solutions d'équations indéterminées (de kuttaka).

Shripati

Shripati Mishra (1019-1066) a écrit les livres Siddhanta Shekhara , un ouvrage majeur sur l'astronomie en 19 chapitres, et Ganit tilaka , incomplète arithmétique traité en 125 versets basé sur une œuvre de Shridhara. Il a travaillé principalement sur:

Permutations et combinaisons.
Solution générale de l'équation linéaire simultanée indéterminée.

Il était également l'auteur deDhikotidakarana, un travail de vingt versets sur:

LeDhruvamanasaest une œuvre de 105 versets sur:

Calcul planétaireslongitudes
éclipses.
planétairestransits.

Nemichandra Siddhanta Chakravati

Nemichandra Siddhanta Chakravati (c. 1100) l'auteur d'un traité de mathématiques intituléGome-mat Sarre.

Bhaskara II

Bhaskara II (1114-1185) était un mathématicien astronome qui a écrit un certain nombre de traités importants, à savoir le Siddhanta Shiromani , Lilavati , Bijaganita , Gola Addhaya , Griha Ganitam et Karan Kautoohal . Un certain nombre de ses contributions ont ensuite été transmis au Moyen-Orient et en Europe. Ses contributions incluent:

Arithmétique:

calcul d'intérêt.
Progressions arithmétiques et géométriques.
géométrie plane.
Géométrie solide.
L'ombre de la gnomon.
Solutions de combinaisons.
A donné une preuve de la division parzéroêtreinfini.

Algèbre:

La reconnaissance d'un nombre positif ayant deux racines carrées.
Sourdes.
Opérations avec des produits de plusieurs inconnues.
Les solutions consistant à:
- Équations du second degré.
- Équations cubiques.
- Équations du quatrième degré.
- Les équations ayant plus d'une inconnue.
- Équations du second degré avec plus d'une inconnue.
- La forme générale del'équation de Pell utilisant le chakravalaméthode.
- L'équation quadratique générale et indéterminée en utilisant lechakravalaméthode.
- Équations cubiques indéterminée.
- Équations quartiques indéterminée.
- Indéterminée ordre supérieurpolynômeséquations.

Géométrie:

A donné une preuve de lathéorème de Pythagore.

Calcul:

Conçue le calcul différentiel.
Découvert ledérivé.
Découvert lecoefficient différentiel.
Développé différenciation.
A déclaréle théorème de Rolle, un cas particulier de lathéorème de la moyenne (l'un des plus importants théorèmes de calcul et d'analyse).
Dérivé l'écart de la fonction sinus.
Calculéπ, correcte à 5 décimales.
Calculé la longueur de la révolution de la Terre autour du Soleil à 9 décimales.

Trigonométrie:

Développements detrigonométrie sphérique
Les formules trigonométriques:
- $\ \sin(a+b)=\sin(a) \cos(b) + \sin(b) \cos(a)$
- $\ \sin(a-b)=\sin(a) \cos(b) - \sin(b) \cos(a)$

Kerala Mathématiques (1300 - 1600)

Le L'école du Kerala de l'astronomie et les mathématiques a été fondée par Madhava de Sangamagrama dans Kerala , Inde du Sud et comptait parmi ses membres: Parameshvara, Neelakanta Somayaji, Jyeshtadeva, Achyuta Pisharati, Melpathur Narayana Bhattathiri et Achyuta Panikkar. Elle a prospéré entre les 14e et 16e siècles et les découvertes originales de l'école semble avoir pris fin avec Narayana Bhattathiri ( 1559- 1632). En tentant de résoudre des problèmes astronomiques, les astronomes de l'école du Kerala indépendamment créé un certain nombre de concepts mathématiques importants. Les résultats les plus importants, expansion de série pour les fonctions trigonométriques , ont été donnés en sanscrit verset dans un livre par Neelakanta appelé Tantrasangraha et un commentaire sur ce travail appelés Tantrasangraha-vakhya l'auteur est inconnu. Les théorèmes ont été formulées sans preuve, mais les preuves pour la série pour sine , cosinus , et inverse tangente ont été fournis un siècle plus tard dans le travail Yuktibhasa (c.1500-c.1610), écrit en malayalam, par Jyesthadeva, et aussi dans un commentaire sur Tantrasangraha .

Leur découverte de ces trois développements en séries importantes de calcul -plusieurs siècles avant le calcul a été développé en Europe par Isaac Newton et Gottfried Leibniz -Est une réalisation historique dans les mathématiques. Cependant, l'école du Kerala ne peut pas être dit avoir inventé le calcul , parce que, alors qu'ils étaient en mesure de développer Taylor développements en série pour les fonctions trigonométriques importantes, ils ont développé ni une théorie complète de la différenciation ou l'intégration , ni le théorème fondamental du calcul . Les résultats obtenus par l'école Kerala comprennent:

Le (infinie)série géométrique: 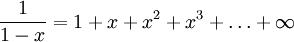$\frac{1}{1-x} = 1 + x + x^2 + x^3 + \dots + \infty$ pour $|x|<1$ Cette formule était déjà connu, par exemple, dans les travaux du mathématicien arabe du 10ème siècleAlhazen (la forme latinisée du nom Ibn Al-Haytham (965-1039)).
Une preuve semi-rigoureux (voir «induction» remarque ci-dessous) du résultat: $1^p+ 2^p + \cdots + n^p \approx \frac{n^{p+1}}{p+1}$ pour les grands n . Ce résultat a été également connu pour Alhazen.
Utilisation intuitive del'induction mathématique, cependant, l' hypothèse de récurrencen'a pas été formulée ou employé dans les preuves.
Applications d'idées de (ce qui allait devenir) différentiel et intégralcalculpour obtenir(Taylor-Maclaurin) série infiniepour $\sin x$ , $\cos x$ Et $\arctan x$ LeTantrasangraha-vakhyadonne la série en vers, qui, lorsqu'il est traduit en notation mathématique, peut être écrite comme:

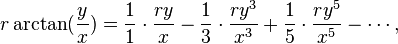$r\arctan(\frac{y}{x}) = \frac{1}{1}\cdot\frac{ry}{x} -\frac{1}{3}\cdot\frac{ry^3}{x^3} + \frac{1}{5}\cdot\frac{ry^5}{x^5} - \cdots ,$ où $y/x \leq 1.$

$\sin x = x - x\cdot\frac{x^2}{(2^2+2)r^2} + x\cdot \frac{x^2}{(2^2+2)r^2}\cdot\frac{x^2}{(4^2+4)r^2} - \cdot$

$r - \cos x = r\cdot \frac{x^2}{(2^2-2)r^2} - r\cdot \frac{x^2}{(2^2-2)r^2}\cdot \frac{x^2}{(4^2-4)r^2} + \cdots ,$ où, pour $r = 1$ , réduire la série à la série de puissance standard pour ces fonctions trigonométriques, par exemple:

- $\sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots$ et
- $\cos x = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \cdots$
Utilisation de rectification (calcul de longueur) de l'arc de cercle pour donner une preuve de ces résultats. (La méthode de Leibniz plus tard, en utilisant quadrature ( c.-à- calcul de l'aire sous l'arc de cercle, a été pas utilisé.)
L'utilisation de l'expansion de série de $\arctan x$ d'obtenir une expression de série infinie (plus tard connu comme la série Gregory) pour $\ Pi$ :

$\frac{\pi}{4} = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \ldots + \infty$

Une approximation rationnelle de l' erreur pour la somme finie de leur série d'intérêt. Par exemple, l'erreur $f_i(n+1)$ (pour n impair, et i = 1, 2, 3 ) de la série:

$\frac{\pi}{4} \approx 1 - \frac{1}{3}+ \frac{1}{5} - \cdots (-1)^{(n-1)/2}\frac{1}{n} + (-1)^{(n+1)/2}f_i(n+1)$

où $f_1(n) = \frac{1}{2n}, \ f_2(n) = \frac{n/2}{n^2+1}, \ f_3(n) = \frac{(n/2)^2+1}{(n^2+5)n/2}.$

Manipulation du terme d'erreur pour dériver une série convergente plus rapide pour $\ Pi$ :

$\frac{\pi}{4} = \frac{3}{4} + \frac{1}{3^3-3} - \frac{1}{5^3-5} + \frac{1}{7^3-7} - \cdots \infty$

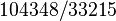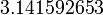
Utilisation de la série améliorée afin de dériver une expression rationnelle, $104348/33215$ pour $\ Pi$ corriger jusqu'àneufdécimales,c.-à- $3.141592653$
Utilisez d'une notion intuitive de limite pour calculer ces résultats.
Un semi-rigoureux (voir la remarque sur les limites ci-dessus) la méthode de différenciation de certaines fonctions trigonométriques. Cependant, ils ne formuler la notion de fonction , ou avoir connaissance des fonctions exponentielles ou logarithmiques.

Les travaux de l'école du Kerala ont d'abord été écrits pour le monde occidental par l'Anglais CM Whish en 1835 . Selon Whish, les mathématiciens Kerala avaient « jeté les bases d'un système complet de fluxions »et ces œuvres abondé" avec des formes et fluxionnels série se trouve dans aucun travail de pays étrangers. " Cependant, les résultats de Whish ont été presque complètement négligés, jusqu'à ce que plus d'un siècle plus tard, quand les découvertes de l'école du Kerala ont été étudiées à nouveau par C. Rajagopal et ses associés. Leur travail comprend des commentaires sur les épreuves de la série arctan dans Yuktibhasa donné dans deux documents, un commentaire sur le 'Yuktibhasa preuve s de la série de sinus et cosinus et deux documents qui fournissent les sanskrits versets du Tantrasangrahavakhya pour la série pour arctan, le péché , et le cosinus (avec traduction anglaise et commentaire).

Les mathématiciens Kerala inclus Narayana Pandit (c. 1340-1400), qui a composé deux œuvres, un traité d'arithmétique, Ganita Kaumudi , et un traité algébrique, Bijganita Vatamsa . Narayana est aussi pensé pour être l'auteur d'un commentaire élaborée de Bhaskara II Lilavati, intitulé Karmapradipika (ou Karma-Paddhati ). Madhava de Sangamagramma (c. 1340-1425) fut le fondateur de l' école du Kerala. Bien qu'il soit possible qu'il écrivit Karana Paddhati un ouvrage écrit quelque part entre 1375 et 1475, tout ce que nous savons vraiment de son travail provient de travaux des spécialistes ultérieures.

Parameshvara (c. 1370-1460) a écrit des commentaires sur les travaux de Bhaskara I, Aryabhata et Bhaskara II. sa Lilavati Bhasya , un commentaire sur de Bhaskara II Lilavati , contient l'un de ses importantes découvertes: une version du valeur moyenne théorème. Nilakantha Somayaji (1444-1544) a composé le Tantra Samgraha (qui ' engendré «un commentaire anonyme tard Tantrasangraha-vyakhya et un autre commentaire par le nom Yuktidipaika , écrit en 1501). Il a élaboré et étendu les contributions de Madhava.

Citrabhanu (c. 1530) était un mathématicien du 16ème siècle du Kerala qui a donné solutions entières à 21 types de systèmes de deux équations algébriques simultanées à deux inconnues. Ces types de toutes les paires possibles de sept équations des formes suivantes:

$\ x + y = a, x - y = b, xy = c, x^2 + y^2 = d, x^2 - y^2 = e, x^3 + y^3 = f, x^3 - y^3 = g$

Pour chaque cas, Citrabhanu a donné une explication et une justification de son règne ainsi que d'un exemple. Certains de ses explications sont algébrique, tandis que d'autres sont géométriques. Jyesthadeva (c. 1500-1575) était un autre membre de l'École Kerala. Son travail a été la clé Yukti-bhasa (écrit en malayalam, la langue régionale du Kerala ). Jyesthadeva présenté des preuves de la plupart des théorèmes mathématiques et série infinie précédemment découverts par Madhava et d'autres mathématiciens Kerala scolaires.

Les accusations de l'eurocentrisme

Il a été suggéré que les contributions aux mathématiques indiennes ont pas été dûment accusé dans l'histoire moderne et que de nombreuses découvertes et inventions par les mathématiciens indiens sont actuellement attribués culturellement à leurs homologues occidentaux, à la suite de l'eurocentrisme. Selon Joseph GG:

[Leur travail] prend en compte certaines des objections soulevées à propos de la trajectoire eurocentrique classique. La prise de conscience [des mathématiques indiennes et arabe] est trop susceptible d'être tempérée par le rejet dédaigneux de leur importance par rapport aux mathématiques grecques. Les contributions d'autres civilisations - notamment la Chine et l'Inde, sont perçus soit comme des emprunteurs à partir de sources grecques ou ayant fait seulement des contributions mineures au développement mathématique mainstream. Une ouverture aux résultats des recherches les plus récentes, en particulier dans le cas des mathématiques indiennes et chinoises, est malheureusement manquant "

L'historien des mathématiques,Florian Cajori, a suggéré qu'il "doutait [s] queDiophante a obtenu son premier aperçu de la connaissance algébrique de l'Inde. "

Plus récemment, comme expliqué dans la section ci-dessus, la série infinie de calcul pour les fonctions trigonométriques (redécouvert par Gregory, Taylor et Maclaurin à la fin du 17ème siècle) ont été décrits (avec des preuves) en Inde, par des mathématiciens de l' école du Kerala, remarquablement quelques deux siècles plus tôt. Certains chercheurs ont récemment suggéré que la connaissance de ces résultats aurait été transmis à l'Europe par la voie du commerce de Kerala par les commerçants et les missionnaires jésuites. Kerala était en contact permanent avec la Chine et l'Arabie, et, à partir d'environ 1500, avec l'Europe. L'existence de voies de communication et une chronologie appropriée certainement faire une telle transmission une possibilité. Cependant, il n'y a aucune preuve directe par voie de manuscrits pertinents qu'une telle transmission a effectivement eu lieu. En effet, selon David Bressoud, "il n'y a aucune preuve que le travail indien de série a été connu au-delà de l'Inde, ou même à l'extérieur du Kerala, jusqu'au XIXe siècle."

Les deux savants arabes et indiens ont fait des découvertes avant la 17ème siècle qui sont maintenant considéré comme une partie du calcul. Cependant, ils ne pouvaient pas, comme Newton et Leibniz étaient, à "combiner plusieurs idées différentes sous les deux thèmes fédérateurs de la dérivée et l' intégrale , montrer le lien entre les deux, et tourner dans le calcul excellent outil de résolution de problème, nous ont aujourd'hui ". Les carrières intellectuelles des deux Newton et Leibniz sont bien documentés et il n'y a aucune indication de leur travail ne pas être leur propre; Cependant, on ne sait pas avec certitude si les immédiats prédécesseurs de Newton et Leibniz », y compris, en particulier, Fermat et de Roberval, a appris de certaines des idées des mathématiciens islamiques et indiennes par des sources nous ne sommes pas conscients maintenant." Ceci est un domaine de recherche actif en cours, en particulier dans les manuscrits des collections de l'Espagne et du Maghreb , de la recherche qui est actuellement poursuivi, entre autres, au Centre National de Recherche Scientifique dans Paris .

Récupéré à partir de " http://en.wikipedia.org/w/index.php?title=Indian_mathematics&oldid=197000390 "