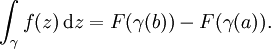Théorème fondamental du calcul
Renseignements généraux
Cette sélection écoles a été choisi par SOS Enfants pour les écoles dans le monde en développement ne ont pas accès à Internet. Il est disponible en téléchargement intranet. SOS Children travaille dans 45 pays africains; pouvez-vous aider un enfant en Afrique ?
Le théorème fondamental du calcul précise la relation entre les deux opérations centrales de calcul , la différenciation et l'intégration .
La première partie du théorème, parfois appelé le premier théorème fondamental du calcul, montre qu'un l'intégration indéterminée peut être inversée par une différenciation.
La deuxième partie, parfois appelé le deuxième théorème fondamental du calcul, permet de calculer l' intégrale définie d'une fonction à l'aide de l'un de ses infinité primitives. Cette partie du théorème a des applications pratiques précieux, car il simplifie considérablement le calcul des intégrales définies.
La première déclaration publiée et la preuve d'une version restreinte du théorème fondamental était par James Gregory (1638-1675). Isaac Barrow se est avéré la première version complètement générale du théorème, tout en étudiant de Barrow Isaac Newton (1643-1727) a complété le développement de la théorie mathématique environnante. Gottfried Leibniz (1646-1716) a systématisé la connaissance dans un calcul des quantités infinitésimales.
Intuition
Intuitivement, le théorème affirme simplement que la somme de modifications infinitésimales dans une quantité au fil du temps (ou une autre quantité) se ajoutent à la variation nette de la quantité.
Pour comprendre cette déclaration, nous allons commencer avec un exemple. Supposons une particule se déplace en ligne droite avec sa position donnée par x (t) où t est le temps et x (t) signifie que x est une fonction de t. Le dérivé de cette fonction est égale à la variation en quantité infinitésimale, d x, par changement infime dans le temps, d t (bien sûr, le dérivé lui-même dépend du temps). Définissons ce changement dans la distance par changement dans le temps que la vitesse v de la particule. En Notation de Leibniz:
Réorganisation de cette équation, il se ensuit que:
Par la logique ci-dessus, un changement de x (  ) Est la somme des changements infinitésimaux d x. Il est également égale à la somme des produits infinitésimales du dérivé et du temps. Cette sommation infinie est l'intégration; par conséquent, l'opération d'intégration permet la récupération de la fonction d'origine à partir de son dérivé. Comme on peut raisonnablement déduire, cette opération fonctionne en sens inverse que nous pouvons différencier le résultat de notre intégrante de récupérer le dérivé d'origine.
) Est la somme des changements infinitésimaux d x. Il est également égale à la somme des produits infinitésimales du dérivé et du temps. Cette sommation infinie est l'intégration; par conséquent, l'opération d'intégration permet la récupération de la fonction d'origine à partir de son dérivé. Comme on peut raisonnablement déduire, cette opération fonctionne en sens inverse que nous pouvons différencier le résultat de notre intégrante de récupérer le dérivé d'origine.
Déclarations officielles
Il ya deux parties au théorème fondamental du calcul. Librement mis, la première partie traite de la dérivé d'un primitive, tandis que les deuxième partie traite de la relation entre primitives et intégrales définies .
Première partie
Cette partie est parfois appelée Première théorème fondamental du calcul.
Soit f une fonction numérique continue définie sur un intervalle fermé [a, b]. Soit F la fonction définie, pour tout x dans [a, b], par
Puis, F est dérivable sur [a, b], et pour tout x dans [a, b],
 .
.
L'opération 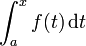 est une intégrale définie par la limite supérieure variable et son résultat F (x) est l'un des nombreux infiniment primitives de f.
est une intégrale définie par la limite supérieure variable et son résultat F (x) est l'un des nombreux infiniment primitives de f.
Deuxième partie
Cette partie est parfois appelée Deuxième théorème fondamental du calcul.
Soit f une fonction numérique continue définie sur un intervalle fermé [a, b]. Soit F une primitive de f, ce est l'un des infiniment nombreuses fonctions telles que, pour tout x dans [a, b],
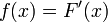 .
.
Puis
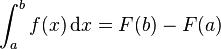 .
.
Corollaire
Soit f une fonction réelle définie sur un intervalle fermé [a, b]. Soit F une fonction telle que, pour tout x dans [a, b],
Alors, pour tout x dans [a, b],
et
 .
.
Exemples
A titre d'exemple, supposons que vous devez calculer
Ici,  et nous pouvons utiliser
et nous pouvons utiliser  que la primitive. Par conséquent:
que la primitive. Par conséquent:
Ou, plus généralement, supposons que vous devez calculer
Ici,  et nous pouvons utiliser
et nous pouvons utiliser  que la primitive. Par conséquent:
que la primitive. Par conséquent:
Mais ce résultat aurait pu être trouvé beaucoup plus facilement que
Preuve
Supposer que
Soit deux nombres x 1 et x 1 + Δ x dans [a, b]. Donc, nous avons
et
En soustrayant les deux équations donne
On peut montrer que
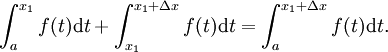
- (La somme des aires des deux régions adjacentes est égale à la zone des deux régions combinées.)
Manipuler cette équation donne
La substitution de ce qui précède (1) entraîne
Selon le signifie théorème de la valeur d'intégration, il existe un en c [x 1, x 1 + Δ x] tels que
 .
.
La substitution de ce qui précède (2) nous obtenons
 .
.
Divisant les deux côtés par Δ x donne

- Notez que l'expression sur le côté gauche de l'équation est Newton différence quotient F en x 1.
Prenez la limite que Δ x → 0 des deux côtés de l'équation.
L'expression sur le côté gauche de l'équation est la définition de la dérivée de F à 1 x.
Pour trouver l'autre limite, nous allons utiliser la Théorème des gendarmes. Le nombre c est dans l'intervalle [x 1, x 1 + Δ x], de sorte que x 1 ≤ c ≤ x 1 + Δ x.
Aussi, 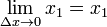 et
et 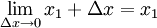 .
.
Par conséquent, d'après le théorème de compression,
Substituant dans (3), nous obtenons
La fonction f est continue en c, de sorte que la limite peut être prise à l'intérieur de la fonction. Par conséquent, on obtient
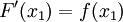 .
.
qui complète la preuve.
(Leithold et al, 1996)
Preuve alternative
Ce est une limite par la preuve Riemann résume.
Soit f continue sur l'intervalle [a, b], et soit F une primitive de f. Commencez par la quantité
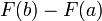 .
.
Qu'il y ait des numéros
- x 1, ..., x n
tel que
 .
.
Il se ensuit que
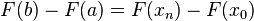 .
.
Maintenant, nous ajoutons chaque F (x i) avec son inverse additif, de sorte que la quantité résultante est égale:
La quantité ci-dessus peut être écrite comme la somme suivante:
Ensuite, nous allons utiliser le valeur moyenne théorème. En résumé,
Soit F continue sur l'intervalle fermé [a, b] et dérivable sur l'intervalle ouvert (a, b). Ensuite, il existe un c dans (a, b) de telle sorte que
Il se ensuit que
La fonction F est dérivable sur l'intervalle [a, b]; par conséquent, il est également différentiable et continue sur chaque intervalle x i -1. Par conséquent, selon le théorème de la valeur moyenne (ci-dessus),
La substitution de ce qui précède (1), on obtient
L'hypothèse implique  Aussi,
Aussi, 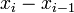 peut être exprimée comme
peut être exprimée comme  de la partition
de la partition  .
.

Notez que nous décrivons l'aire d'un rectangle, avec les temps de largeur la hauteur, et nous ajoutons les régions ensemble. Chaque rectangle, en vertu de la Valeur moyenne théorème, décrit une approximation de la section de la courbe est tirée par dessus. Notez également que 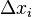 n'a pas besoin d'être le même pour toute valeur de
n'a pas besoin d'être le même pour toute valeur de  Ou en d'autres termes que la largeur des rectangles peuvent différer. Ce que nous avons à faire est de rapprocher la courbe avec
Ou en d'autres termes que la largeur des rectangles peuvent différer. Ce que nous avons à faire est de rapprocher la courbe avec  rectangles. Maintenant, comme la taille des partitions obtenir plus petits et n augmente, résultant en plusieurs partitions pour couvrir l'espace, nous allons nous rapprocher et plus proche de la superficie réelle de la courbe.
rectangles. Maintenant, comme la taille des partitions obtenir plus petits et n augmente, résultant en plusieurs partitions pour couvrir l'espace, nous allons nous rapprocher et plus proche de la superficie réelle de la courbe.
En prenant la limite de l'expression comme la norme des partitions se rapproche de zéro, nous arrivons à la Intégrale de Riemann. Ce est, nous prenons la limite comme le plus grand des partitions tend vers zéro dans la taille, de sorte que toutes les autres partitions sont plus petits et le nombre de partitions tend vers l'infini.
Ainsi, on prend la limite des deux côtés de (2). Cela nous donne
Ni F (b) ni F (a) dépend || Δ ||, de sorte que la limite sur le côté gauche reste F (b) - f (a).
L'expression sur le côté droit de l'équation définit une intégrale sur f de a à b. Par conséquent, on obtient
qui complète la preuve.
Généralisations
Nous ne avons pas besoin d'assumer la continuité de f sur tout l'intervalle. Partie I du théorème dit alors: si f est toute intégrable Lebesgue fonction sur [a, b] et x 0 est un nombre dans [a, b] tel que f est continue en x 0,
est dérivable pour x = x 0 à F '(x 0) = f (x 0). Nous pouvons assouplir les conditions sur f encore et supposons que ce est simplement localement intégrable. Dans ce cas, nous pouvons conclure que la fonction F est différentiable '(x) = presque partout et F f (x) presque partout. Ce est parfois connu comme la différenciation du théorème de Lebesgue.
Partie II du théorème est vrai pour toute fonction intégrable Lebesgue f qui a une primitive F (fonctions intégrables font pas tous, cependant).
La version du Théorème de Taylor qui exprime le terme d'erreur comme une intégrale peut être considérée comme une généralisation du théorème fondamental.
Il existe une version du théorème de complexes fonctions: supposons U est un ouvert de C et f: U → C est une fonction qui a une F primitive holomorphe sur U. Ensuite, pour chaque courbe γ: [a, b] → U, le courbe intégrale peut être calculée comme
Le théorème fondamental peut être généralisée à courbes et de surfaces intégrales de dimensions supérieures et collecteurs .
L'une des déclarations les plus puissants dans cette direction est Théorème de Stokes.
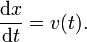
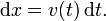
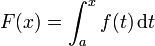
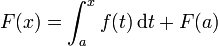
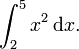
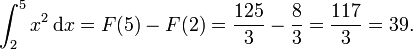
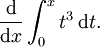

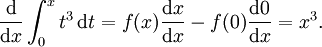

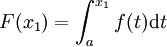
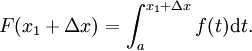

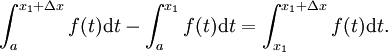

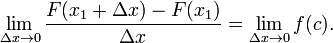

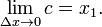

![\ Begin {matrix} F (b) - F (a) & = & F (xn) \, + \, [- F (x_ {n-1}) \, + \, F (x_ {n-1} )] \, + \, \ ldots \, + \, [- F (x 1) + F (x 1)] \, - \, F (x_0) \, \\ & = & [F (xn) \, - \, F (x_ {n-1})] \, + \, [F (x_ {n-1}) \, + \, \ ldots \, - \, F (x 1)] \, + \, [ F (x 1) \, - \, F (x_0)] \, \ end {matrix}](../../images/62/6206.png)
![F (b) - F (a) = \ sum_ {i = 1} ^ n [F (x_i) - F (x_ {i-1})] \ qquad (1)](../../images/62/6207.png)
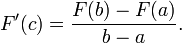
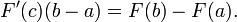

![F (b) - F (a) = \ sum_ {i = 1} ^ n [F '(c_i) (x_i - x_ {i-1})].](../../images/62/6211.png)
![F (b) - F (a) = \ sum_ {i = 1} ^ n [f (c_i) (\ Delta x_i)] \ qquad (2)](../../images/62/6215.png)
![\ Lim _ {\ | \ Delta \ | \ 0} F (b) - F (a) = \ lim _ {\ | \ Delta \ | \ 0} \ sum_ {i = 1} ^ n [f (c_i) (\ Delta x_i)] \ ,.](../../images/62/6225.png)
![F (b) - F (a) = \ lim _ {\ | \ Delta \ | \ 0} \ sum_ {i = 1} ^ n [f (c_i) (\ Delta x_i)]](../../images/62/6226.png)