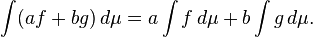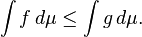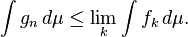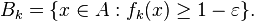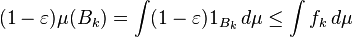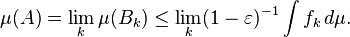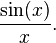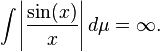L'intégration de Lebesgue
Renseignements généraux
SOS Enfants produite ce site pour les écoles ainsi que ce site de vidéo sur l'Afrique . Cliquez ici pour en savoir plus sur le parrainage d'enfants.

En mathématiques , le intégrante d'un non-négative fonction peut être considérée dans le cas le plus simple que l' espace entre le . graphe de cette fonction et l'intégration axe x Lebesgue est une construction mathématique qui se étend de la partie intégrante d'une plus grande classe de fonctions; elle se étend également le domaines sur lesquels ces fonctions peuvent être définis. Il avait compris depuis longtemps que pour les fonctions non-négatifs avec un graphe assez lisse (comme fonctions continues sur fermé délimitée intervalles) l'aire sous la courbe pourrait être définie comme l'intégrale et calculés en utilisant des techniques de rapprochement de la région en polygones . Cependant, comme la nécessité d'envisager des fonctions plus irréguliers née (par exemple, à la suite des limitant les processus de l'analyse mathématique et mathématique théorie des probabilités ), il est devenu clair que les techniques d'approximation plus prudent seraient nécessaires pour définir une intégrale approprié. Aussi, nous pourrions le souhaiter à intégrer sur des espaces plus généraux que la droite réelle; l'intégrale de Lebesgue fournit les bonnes abstractions nécessaires pour faire ce travail important.
L'intégrale de Lebesgue joue un rôle important dans la branche des mathématiques appelée analyse réelle et dans de nombreux autres domaines des sciences mathématiques, et est nommé d'après Henri Lebesgue (1875-1941) qui a introduit l'intégrale (Lebesgue 1904). Ce est aussi une partie de pivotement de la théorie axiomatique des probabilités.
Le terme «intégration de Lebesgue" peut se référer soit à la théorie générale de l'intégration d'une fonction par rapport à un général mesurer, tel que présenté par Lebesgue, ou pour le cas spécifique de l'intégration d'une fonction définie sur un sous-domaine de la réelle ligne par rapport à Mesure de Lebesgue.
Introduction
L'intégrale d'une fonction f entre les limites a et b peut être interprété comme l'aire sous la courbe de f. Ce est facile à comprendre pour les fonctions familières telles que polynômes , mais ce que cela signifie pour des fonctions plus exotiques? En général, ce est la classe des fonctions pour lesquelles "aire sous la courbe« fait sens? La réponse à cette question a une grande importance théorique et pratique.
Dans le cadre d'un mouvement général vers rigueur en mathématiques au XIXe siècle, des tentatives ont été faites pour mettre le calcul intégral sur des bases solides. Le Intégrale de Riemann, proposé par Bernhard Riemann (1826-1866), est une tentative largement réussie de fournir une telle fondation. La définition de Riemann commence par la construction d'une séquence de zones facilement calculées qui convergent à l'intégrale d'une fonction donnée. Cette définition est retenue dans le sens que lui donne la réponse attendue pour de nombreux problèmes déjà résolus, et donne des résultats utiles à de nombreux autres problèmes.
Cependant, l'intégration de Riemann ne interagit pas bien avec la prise de séquences de limites de fonctions, ce qui rend ces procédés limitatifs difficiles à analyser. Ceci est d'une importance primordiale, par exemple, dans l'étude de série de Fourier, transformées de Fourier et d'autres sujets. L'intégrale de Lebesgue est mieux en mesure de décrire comment et quand il est possible de prendre des limites sous le signe intégrante. La définition de Lebesgue considère une classe différente de zones facilement calculés que la définition de Riemann, qui est la principale raison de l'intégrale de Lebesgue est mieux comporté. La définition de Lebesgue permet également de calculer des intégrales pour une classe plus large de fonctions. Par exemple, le Fonction de Dirichlet, qui est 0 où son argument est irrationnelle et une autre, a une intégrale de Lebesgue, mais il n'a pas une intégrale de Riemann.
L'approche de Lebesgue à l'intégration a été résumée dans une lettre à Paul Montel. Il écrit:
Je dois payer une certaine somme, ce que je ai recueilli dans ma poche. Je prends les billets et les pièces de ma poche et je leur donne au créancier dans l'ordre je les trouve jusqu'à ce que je ai atteint la somme totale. Ce est l'intégrale de Riemann. Mais je peux procéder différemment. Après je ai pris tout l'argent de ma poche je commander les billets et les pièces en fonction de valeurs identiques, puis-je payer les tas plusieurs l'un après l'autre pour le créancier. Ce est ma intégrante.- Source: (Siegmund-Schultze 2008)
L'idée est que l'on devrait être en mesure de réorganiser les valeurs d'une fonction librement tout en préservant la valeur de l'intégrale. Ce processus de réarrangement peut convertir une fonction très pathologique dans l'une qui est «gentil» du point de vue de l'intégration, et permet ainsi à ces fonctions pathologiques à intégrer.
Interprétation intuitive

Pour obtenir une intuition sur les différentes approches de l'intégration, imaginons que l'on souhaite de trouver le volume de la montagne (au dessus du niveau de la mer).
- L'approche de Riemann-Darboux
- Divisez la base de la montagne en une grille de 1 mètre carrés. Mesurer l'altitude de la montagne au centre de chaque carré. Le volume sur un carré de la grille unique est d'environ 1 × 1 × (altitude), de sorte que le volume total est la somme des altitudes.
- L'approche de Lebesgue
- Dessine un contour carte de la montagne, où les contours adjacentes sont 1 mètre d'altitude en dehors. Le volume de la terre contenue dans un seul contour est d'environ les temps de la région de ce contour 1, de sorte que le volume total est la somme de ces zones parfois 1 mètre.
Folland résume la différence entre le Riemann et Lebesgue approches ainsi: "pour calculer l'intégrale de Riemann de f, on partitionne le domaine [a, b] en sous-intervalles", tandis que dans l'intégrale de Lebesgue, "une est en vigueur partitionner la gamme de f ».
Vers une définition formelle
Pour définir l'intégrale de Lebesgue nécessite formellement la notion de mesure qui, en gros, associés à chaque ensemble A de nombres réels d'un nombre non négatif μ (A) représentant la "taille" de A. Cette notion de «taille» doit concorder avec la longueur habituelle d'un intervalle ou réunion disjointe d'intervalles. Supposons que f: R → R est une fonction à valeurs réelles non-négative. Utilisation du "partage de la gamme de f" la philosophie, l'intégrale de f doit être la somme sur t des zones entre une bande horizontale mince entre y = t et y = t + dt. Cette zone est juste
Laisser
L'intégrale de Lebesgue de f est alors définie par
où l'intégrale sur la droite est une mauvaise ordinaire intégrale de Riemann (noter que f * est une fonction positive strictement décroissante, et a donc une mauvaise Riemann bien définie intégrante). Pour une classe de fonctions approprié (la fonctions mesurables) Cela définit l'intégrale de Lebesgue.
Un générale (pas nécessairement positive) fonction f est intégrable Lebesgue si la zone entre le graphe de f et la axe des x est fini:
Dans ce cas, l'intégrale est, comme dans le cas de Riemann, la différence entre la zone au-dessus de l'axe des x et la région en dessous de la axe des x:
où
Construction

La discussion qui suit en parallèle l'approche déclaratif plus courante de l'intégrale de Lebesgue. Dans cette approche, la théorie de l'intégration comprend deux parties distinctes:
- Une théorie des ensembles mesurables et des mesures sur ces ensembles.
- Une théorie des fonctions intégrales et mesurables sur ces fonctions.
La fonction dont l'intégrale se trouve est alors approchée par certains soi-disant fonctions simples, dont les intégrales peut être écrite en termes de la mesure. L'intégrale de la fonction d'origine est alors la limite de l'intégrale des fonctions simples.
Théorie de la mesure
Théorie de la mesure a été initialement créé pour fournir une abstraction utile de la notion de longueur de sous-ensembles de la ligne réelle et, plus généralement, la superficie et le volume de sous-ensembles d'espaces euclidiens. En particulier, il a fourni une réponse systématique à la question qui sous-ensembles de R ont une longueur. Comme l'a montré par les développements ultérieurs dans la théorie des ensembles (voir ensemble non mesurable), il est effectivement impossible d'assigner une longueur à tous les sous-ensembles de R d'une manière qui préserve certaines propriétés d'additivité et la traduction invariance naturelles. Cela suggère que la cueillette à une classe appropriée de sous-ensembles mesurables est une condition essentielle.
L'intégrale de Riemann utilise la notion de longueur explicitement. En effet, l'élément de calcul de l'intégrale de Riemann est le rectangle [a, b] × [c, d], dont la surface est fixée à (b - a) (d - c). La quantité b - a est la longueur de la base du rectangle et d - c est la hauteur du rectangle. Riemann ne pouvait utiliser rectangles planes de rapprocher l'aire sous la courbe parce qu'il n'y avait pas de théorie adéquate pour mesurer ensembles plus généraux.
Dans le développement de la théorie dans la plupart des manuels modernes (après 1950), l'approche de mesurer et d'intégration est axiomatique. Cela signifie qu'une mesure est une fonction μ définie sur une certaine classe X de parties d'un ensemble E, qui satisfait à une certaine liste de propriétés. Ces propriétés peuvent être présentés à tenir dans de nombreux cas différents.
Intégration
Nous commençons avec un mesure l'espace (E, X, μ) où E est un ensemble , X est un σ-algèbre des sous-ensembles de E et μ est une (non négative) mesurer sur E, défini sur les ensembles de X.
Par exemple, E peut être euclidien n -espace R n ou un Lebesgue partie mesurable de celui-ci, X sera le σ-algèbre de tous les sous-ensembles mesurables Lebesgue de E, et μ sera le Mesure de Lebesgue. Dans la théorie mathématique des probabilités, nous limitons notre étude à une probabilité mesure μ, ce qui satisfait μ (E) = 1.
Dans la théorie de Lebesgue, intégrales sont définies pour une classe de fonctions appelé fonctions mesurables. Une fonction f est mesurable si la pré-image de chaque intervalle de la forme (t, ∞) est dans X:
On peut montrer que ceci est équivalent à exiger que la pré-image de tout Borel sous-ensemble de R soit en X. Nous ferons cette hypothèse désormais. L'ensemble des fonctions mesurables est fermé sous opérations algébriques, mais plus important encore la classe est fermé sous différents types de ponctuelle limites séquentielles:
sont mesurables si la séquence originale k (f k), où k ∈ N, composé des fonctions mesurables.
Nous construisons une intégrale
pour les fonctions réelles mesurables f définie sur E par étapes:
fonctions Indicateurs: Pour attribuer une valeur à l'intégrale de la fonction indicatrice 1 S d'un ensemble mesurable S conforme à la mesure donnée μ, le seul choix raisonnable est de mettre:
Notez que le résultat peut être égal à + ∞, à moins que μ est une mesure limitée.
Des fonctions simples: Un finie combinaison linéaire de fonctions indicatrices
où les coefficients a k sont des nombres réels et k des ensembles sont mesurables, est appelé un mesurables fonction simple. Nous étendons la linéarité intégrale par des fonctions simples mesurables non-négatifs. Lorsque les coefficients a k sont non-négatif, nous avons mis en
La convention 0 × ∞ = 0 doit être utilisé, et le résultat peut être infinie. Même si une fonction simple peut être écrit à bien des égards comme une combinaison linéaire de fonctions de l'indicateur, l'intégrale sera toujours la même; ce qui peut être montré en utilisant la propriété d'additivité de mesures.
Certains soins sont nécessaires pour définir l'intégrale d'une fonction à valeurs réelles simple, pour éviter l'expression undefined ∞ - ∞: on suppose que la représentation
est telle que μ (S k) <∞ k chaque fois qu'un ≠ 0. Alors la formule ci-dessus pour l'intégrale de f est logique, et le résultat ne dépend pas de la représentation particulière de f satisfaisant aux hypothèses.
Si B est un sous-ensemble mesurable de E et S est une fonction simple mesurables définit une
Les fonctions non-négatifs: Soit f une fonction mesurable non-négatif sur E qui nous permettons d'atteindre la valeur + ∞, en d'autres termes, f prend des valeurs non-négatives dans le étendue réelle ligne de numéro. Nous définissons
Nous devons montrer cela coïncide solidaires de la précédente, définie sur l'ensemble des fonctions simples. Lorsque E est un segment [a, b], il ya aussi la question de savoir si cela correspond en aucune façon à une notion d'intégration de Riemann. Il est possible de prouver que la réponse aux deux questions est oui.
Nous avons défini l'intégrale de f pour toute fonction mesurable non négatif étendu valeur réelle sur E. Pour certaines fonctions, cette intégrale ∫ E f dμ sera infinie.
Fonctions signés: Pour gérer les fonctions signés, nous avons besoin de quelques définitions. Si f est une fonction mesurable de l'ensemble E pour les réels (y compris ± ∞), alors nous pouvons écrire
où
Notez que les deux f + f - sont des fonctions non-négatifs mesurables. Notez également que
Nous disons que l'intégrale de Lebesgue de la fonction mesurable f existe, ou est défini si au moins l'un des  et
et  est fini:
est fini:
Dans ce cas, nous définissons
Si
nous disons que f est intégrable Lebesgue.
Il se avère que cette définition donne les propriétés souhaitables de l'intégrale.
Complexes fonctions valeur peuvent être intégrés de manière similaire, en tenant compte de la partie réelle et la partie imaginaire séparément.
Exemple
Considérons le fonction indicatrice des nombres rationnels, 1 Q. Cette fonction est nulle part constante.
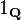 ne est pas de Riemann-intégrable sur [0,1]: Peu importe comment l'ensemble [0,1] est divisé en sous-intervalles, chaque partition contient au moins un rationnel et au moins un nombre irrationnel, parce rationnels et irrationnels sont à la fois dense dans les réels. Ainsi la partie supérieure Darboux sommes seront tous soient un, et les sommes de Darboux inférieurs seront tous zéro.
ne est pas de Riemann-intégrable sur [0,1]: Peu importe comment l'ensemble [0,1] est divisé en sous-intervalles, chaque partition contient au moins un rationnel et au moins un nombre irrationnel, parce rationnels et irrationnels sont à la fois dense dans les réels. Ainsi la partie supérieure Darboux sommes seront tous soient un, et les sommes de Darboux inférieurs seront tous zéro.
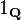 est Lebesgue-intégrable sur [0,1] en utilisant la Mesure de Lebesgue: En effet ce est la fonction de l'indicateur des rationnels donc, par définition
est Lebesgue-intégrable sur [0,1] en utilisant la Mesure de Lebesgue: En effet ce est la fonction de l'indicateur des rationnels donc, par définition
- parce Q est dénombrable.
Domaine de l'intégration
Un problème technique dans l'intégration de Lebesgue est que le domaine de l'intégration est définie comme un ensemble (un sous-ensemble d'un espace de mesure), sans notion d'orientation. Dans le calcul élémentaire, on définit l'intégration par rapport à un Orientation:
En généralisant ce à des dimensions supérieures donne intégration de formes différentielles. En revanche, l'intégration de Lebesgue fournit une généralisation de remplacement, en intégrant sur des sous-ensembles par rapport à une mesure; cela peut être notée comme
pour indiquer l'intégration sur un sous-ensemble A. Pour plus de détails sur la relation entre ces généralisations, voir Forme différentielle: Relation avec les mesures.
Limites de l'intégrale de Riemann
Ici, nous discutons les limites de l'intégrale de Riemann et la plus grande possibilités offertes par l'intégrale de Lebesgue. Nous présumons une compréhension pratique de la Intégrale de Riemann.
Avec l'avènement de série de Fourier, de nombreux problèmes analytiques impliquant intégrales venu dont la solution satisfaisante nécessaire échangeant processus limites et les signes intégrales. Cependant, les conditions dans lesquelles les intégrales
sont égaux révélé très difficile à atteindre dans le cadre de Riemann. Il ya quelques autres difficultés techniques avec l'intégrale de Riemann. Ils sont liés à la difficulté de prise limite décrite ci-dessus.
Échec de la convergence monotone. Comme indiqué plus haut, la fonction de l'indicateur 1 Q sur les rationnels ne est pas Riemann intégrable. En particulier, la Théorème de convergence monotone échoue. Pour comprendre pourquoi, laissez un {k} une énumération de tous les nombres rationnels dans [0,1] (ils sont dénombrable si cela peut être fait.) Ensuite, laissez
La fonction g k est nul partout sauf sur un ensemble fini de points, d'où son intégrale de Riemann est nul. La séquence g k est clairement non-négatif et croissant de manière monotone à une Q, qui ne est pas intégrable Riemann.
Inaptitude à intervalles non bornés. L'intégrale de Riemann ne peut intégrer des fonctions sur un intervalle borné. Il peut cependant être étendue à des intervalles non bornés en prenant limites, tant que cela ne donne pas une réponse comme ∞-∞.
L'intégration des structures autres que l'espace euclidien. L'intégrale de Riemann est inextricablement liée à la structure d'ordre de la ligne.
Théorèmes de base de l'intégrale de Lebesgue
L'intégrale de Lebesgue ne fait pas de distinction entre les fonctions qui ne diffèrent que sur un ensemble de μ-mesure nulle. Pour faire cette précision, les fonctions f et g sont dits être égal presque partout (ae) si
- Si f, g sont des fonctions mesurables non-négatifs (en supposant éventuellement la valeur + ∞) tels que f = g presque partout, puis
À savoir, l'intégrale respecte la relation d'équivalence de presque partout l'égalité.
- Si f, g sont des fonctions tel que f = g presque partout, alors f est Lebesgue intégrable si et seulement si g est intégrable Lebesgue, et les intégrales de f et g sont les mêmes si elles existent.
L'intégrale de Lebesgue a les propriétés suivantes:
Linéarité: Si f et g sont des fonctions intégrables Lebesgue et a et b sont des nombres réels, alors af + bg est intégrable et Lebesgue
Monotonie: Si f ≤ g, puis
Théorème de convergence monotone: Supposons {f k} k ∈ N est une séquence de fonctions positives mesurables tels que
Ensuite, la limite simple f de f k est intégrable et Lebesgue
Remarque: la valeur de l'une des intégrales est autorisé à être infinie.
Lemme de Fatou: Si f {k} k ∈ N est une suite de fonctions non-négatifs mesurables, puis
Encore une fois, la valeur de l'une quelconque des intégrales peut être infinie.
Théorème de convergence dominée: Supposons f {k} k ∈ N est une suite de fonctions complexes mesurables avec limite simple f, et il ya une fonction intégrable Lebesgue g (soit g appartient à la espace L 1) de telle sorte que | f k | ≤ g pour tout k.
Alors, f est Lebesgue intégrable et
Techniques de preuve
Pour illustrer quelques-unes des techniques de preuve utilisés dans la théorie de l'intégration de Lebesgue, nous esquissons une preuve de la convergence monotone Lebesgue théorème mentionné ci-dessus. Soit {f k} k ∈ N être une séquence non décroissante de fonctions non-négatifs mesurables et de mettre
Par la propriété de monotonie de l'intégrale, il est immédiat que:
et la limite sur le droit existe, car la séquence est monotone. Nous montrons maintenant l'inégalité dans l'autre sens. Il résulte de la définition de l'intégrale qu'il existe une séquence non décroissante (g n) de fonctions positives simples tels que g et n ≤ f
Par conséquent, il suffit de prouver que pour chaque n ∈ N,
Nous allons montrer que si g est une fonction simple et
presque partout, puis
En divisant la fonction g en ses parties valeur constante, ce qui réduit au cas où g est la fonction indicatrice d'un ensemble. Le résultat que nous avons à prouver est alors
Supposons que A est un ensemble mesurable et {f k} k ∈ N est une séquence non décroissante de fonctions positives mesurables sur E telle que
pour presque tout x ∈ A. Puis
Pour prouver ce résultat, fixer ε> 0 et définir la séquence des ensembles mesurables
Par monotonie de l'intégrale, il se ensuit que pour tout k ∈ N,
Parce que presque tous les x seront en B k pour k assez grand, nous avons
jusqu'à un ensemble de mesure 0. Ainsi par additivité dénombrable de μ, et parce que B k augmente avec k,
Comme cela est vrai pour tout ε positif le résultat suit.
D'autres formulations
Il est possible de développer l'intégrale par rapport à la mesure de Lebesgue sans compter sur la pleine machines de théorie de la mesure. Une telle approche est fourni par le Daniell intégrante.
Il ya aussi une approche alternative au développement de la théorie de l'intégration par le biais de méthodes analyse fonctionnelle. Existe l'intégrale de Riemann pour toute fonction continue f de support compact définie sur R n (ou un sous-ensemble ouvert fixe). Intégrales de fonctions plus générales peuvent être construits à partir de ces intégrales.
Soit C C l'espace de toutes les fonctions continues à support compact à valeurs réelles de R. Définir une norme sur C c par
Alors C c est un espace vectoriel normé (et en particulier, il est un espace métrique.) Tous les espaces métriques ont Hausdorff achèvements, alors laissez L 1 soit son achèvement. Cet espace est isomorphe à l'espace des fonctions intégrables Lebesgue modulo le sous-espace de fonctions intégrale nulle. En outre, l'intégrale de Riemann ∫ est un uniformément continue fonctionnel par rapport à la norme sur C c, qui est dense dans L 1. Ainsi ∫ a une unique extension à tous de L 1. Cette intégrale est précisément l'intégrale de Lebesgue.
Plus généralement, lorsque l'espace de mesure sur lesquels les fonctions sont définies également un localement compact espace topologique (comme ce est le cas avec le nombres réels R), mesure compatible avec la topologie dans un sens approprié ( Mesures de Radon, dont la mesure de Lebesgue est un exemple) une intégrale par rapport à eux peuvent être définis de la même manière, à partir des intégrales de fonctions continues avec support compact. Plus précisément, les fonctions support compact forment un espace vectoriel qui porte un naturel topologie, et un (Radon) mesure est définie comme une constante linéaire fonctionnel sur cet espace. La valeur d'une mesure à une fonction support compact est alors aussi, par définition, l'intégrale de la fonction. On procède ensuite à étendre la mesure (l'intégrale) à des fonctions plus générales par la continuité, et définit la mesure d'un ensemble comme l'intégrale de sa fonction d'indicateur. Ce est l'approche adoptée par Bourbaki (2004) et un certain nombre d'autres auteurs. Pour plus de détails voir Mesures de Radon.
Limitations de Lebesgue
Le but principal de Lebesgue est de fournir une notation intégrante où les limites des intégrales détiennent sous des hypothèses doux. Il n'y a aucune garantie que chaque fonction est intégrable Lebesgue. Il peut arriver que inappropriées (Riemann) intégrales existent pour les fonctions qui ne sont pas intégrable Lebesgue. Un exemple serait
Cette fonction ne est pas intégrable Lebesgue que
D'autre part, il existe aussi une intégrale de Riemann incorrecte et l'intégrale peut être calculée pour être finie. Ne existe pas un concept équivalent de mauvaise intégrale de Lebesgue, car une telle perspective ne est pas nécessaire du point de vue des théorèmes de convergence.



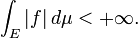


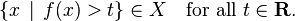








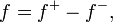

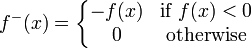
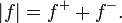



![\ Int _ {[0,1]} 1 _ {\ mathbf Q} \, d \ mu = \ mu (\ mathbf {Q} \ cap [0,1]) = 0,](../../images/2452/245211.png)
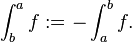
![\ Int_A f \, d \ mu = \ int _ {[a, b]} f \, d \ mu](../../images/2452/245213.png)
![\ Sum_k \ int f_k (x) dx, \ quad \ int \ left [\ sum_k f_k (x) \ right] dx](../../images/2452/245214.png)