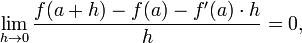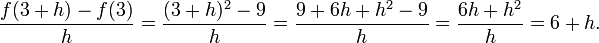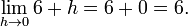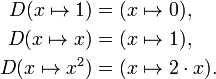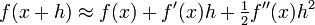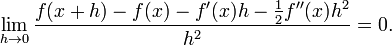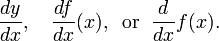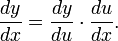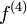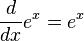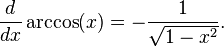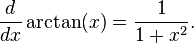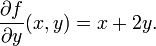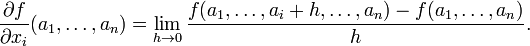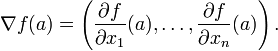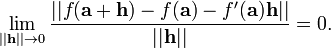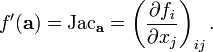Dérivé

Saviez-vous ...

SOS Enfants a essayé de rendre le contenu plus accessible Wikipedia par cette sélection des écoles. Tous les enfants disponibles pour le parrainage de SOS Enfants des enfants sont pris en charge dans une maison de famille près de la charité. Lire la suite ...

Le graphique d'une fonction, dessiné en noir, et une tangente à cette fonction, dessinée en rouge. La pente de la tangente est égale à la dérivée de la fonction au point marqué.

Dans le calcul , une branche de mathématiques , le dérivé est une mesure de la façon dont une fonction change lorsque les valeurs de ses entrées changent. Grosso modo, un dérivé peut être considéré comme combien une quantité est en train de changer à un moment donné. Par exemple, la dérivée de la position ou de distance d'un véhicule à un moment donné dans le temps est la vitesse instantanée ou de vitesse instantanée (respectivement), à laquelle la voiture se déplace (l'inverse du intégrale de la vitesse est la position de la voiture).

Une notion étroitement liée est le différentielle d'une fonction.

La dérivée d'une fonction à une valeur d'entrée choisie décrit le meilleur approximation linéaire de la fonction proche de cette valeur d'entrée. Pour un fonction de valeur réelle d'une seule variable réelle, la dérivée en un point est égal à la pente de la tangente à la graphe de la fonction à ce moment. Dans les dimensions supérieures, la dérivée d'une fonction en un point est un transformation linéaire appelée linéarisation ..

Le processus de recherche d'un dérivé est appelé différenciation. Le théorème fondamental du calcul indique que la différenciation est le processus inverse à l'intégration .

Différenciation et le dérivé

À chaque point, le dérivé est le une pente de ligne qui est tangente à la courbe . La ligne rouge est toujours tangente à la courbe bleue; sa pente est le dérivé.

La différenciation est un procédé pour calculer la vitesse à laquelle une quantité, y, les changements par rapport à la variation d'une autre quantité, x, sur lequel il est dépendante. Ce taux de variation est appelé la dérivée de y par rapport à x. En termes plus précis, la dépendance de y sur x signifie que y est une fonction de x. Si x et y sont des nombres réels , et si le graphique de y est tracée contre x, les mesures les dérivés pente de ce graphique à chaque point. Cette relation fonctionnelle est souvent notée y = f (x), où f représente la fonction.

Le cas le plus simple est lorsque Y est un fonction linéaire de x, ce qui signifie que le graphe de y contre x est une ligne droite. Dans ce cas, y = f (x) = x m + c, pour les nombres réels et m c, m et la pente est donnée par

$m = {\ mbox {} y changer \ over \ mbox {} changer dans x} = {\ Delta y \ over {\ Delta x}}$

où le symbole Δ (la forme majuscule de la lettre grecque Delta) est une abréviation de "changement dans." Cette formule est vrai parce que

Δ y + y = f (x + Δ x) = m (x + Δ x) + c = m x m + c + Δ x = y + x Δ m.

Il en résulte que Δ Δ m y = x.

Cela donne une valeur exacte pour la pente d'une ligne droite. Si la fonction f ne est pas linéaire (ce est à dire son graphique ne est pas une ligne droite), cependant, le changement y divisé par le changement de x varie: la différenciation est une méthode pour trouver une valeur exacte de ce taux de changement à tout donné La valeur de x.

Figure 1. La tangente ligne à (x, f (x))

Figure 2. La sécante à la courbe y = f (x) déterminée par des points (x, f (x)) et (x + h, f (x + h)).

Figure 3. La tangente comme limite de sécantes.

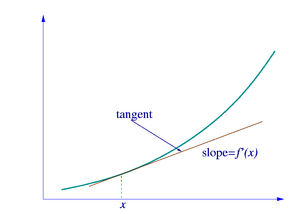
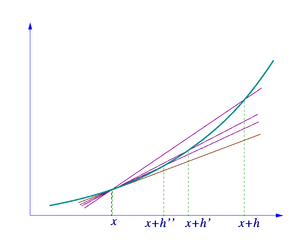
L'idée, illustrée par les figures 1 à 3, consiste à calculer le taux de variation en tant que valeur limite de la rapport des différences Δ Y / Δ x comme Δ x devient infiniment petit.

En Notation de Leibniz, une telle changement infime dans x est notée dx, et le dérivé de y par rapport à x est écrit

$\ Frac {} {dx dy} \, \!$

ce qui suggère le rapport de deux quantités infinitésimales. (L'expression ci-dessus est prononcé dans diverses façons telles que "dy dx" ou "dy sur dx". La forme orale "dydx» est souvent utilisé de la conversation, même si elle peut prêter à confusion.)

L'approche la plus commune pour transformer cette idée intuitive dans une définition précise utilise limites , mais il ya d'autres méthodes, telles que analyse non-standard.

Définition via quotients de différence

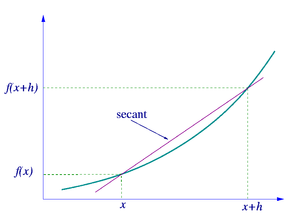
Soit y = f (x) une fonction de x. Dans la géométrie classique, la tangente à un nombre réel a été la ligne unique à travers le point (a, f (a)), qui ne respectait pas le graphe de f transversalement, ce qui signifie que la ligne ne passe pas directement par le graphique. La dérivée de y par rapport à x est à un, géométriquement, la pente de la tangente à la courbe de f en un. La pente de la tangente est très proche de la pente de la droite passant par (a, f (a)) et un point sur le graphe à proximité, par exemple (a + h, f (a + h)). Ces lignes sont appelées droites sécantes. Une valeur de h proche de zéro donnera une bonne approximation de la pente de la tangente, et des valeurs plus petites (en valeur absolue ) de h seront, en général, donner une meilleure approximations. La pente de la sécante est la différence entre les valeurs de y de ces points divisé par la différence entre les valeurs de x, qui est,

$\ Frac {f (a + h) -f (a)} {} h.$

Cette expression est Newton s ' différence quotient. Le dérivé est la valeur du quotient de la différence que les lignes sécantes se rapprocher et plus proche de la ligne tangente. Formellement, la dérivée de la fonction f à un est la limite

$f '(a) = \ lim_ {h \ 0} {f (a + h) -f (a) \ over h}$

du quotient de différence en tant h tend vers zéro, si cette limite existe. Si la limite existe, alors f est différentiable en a. Voici (a) est une f de plusieurs notations communes pour le dérivé ( voir ci-dessous ).

Équivalente, le dérivé satisfait la propriété que

$\ Lim_ {h \ 0} {f (a + h) -f (a) - f '(a) \ cdot h \ over h} = 0,$

qui a l'interprétation intuitive (voir Figure 1) que la tangente à f à une donne le meilleur approximation linéaire

$f (a + h) \ env f (a) + f '(a) h$

à f près d'un (ce est à dire, pour les petits h). Cette interprétation est le plus facile de généraliser à d'autres paramètres ( voir ci-dessous ).

La substitution de 0 à h dans les causes différence de quotient la division par zéro, de sorte que la pente de la tangente ne se trouvent pas directement. Au lieu de cela, définissent Q (h) comme étant le quotient de la différence en fonction de h:

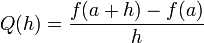$Q (h) = \ frac {f (a + h) - f (a)} {h}$ .

Q (h) est la pente de la droite sécante entre (a, f (a)) et (a + h, f (a + h)). Si f est une fonction continue, ce qui signifie que son graphe est une courbe continue sans écarts, alors Q est une fonction continue loin du point h = 0. Si la limite $\ Textstyle \ lim_ {h \ 0} Q (h)$ existe, ce qui signifie qu'il ya une façon de choisir une valeur pour Q (0) ce qui rend le graphique de Q une fonction continue, alors la fonction f est différentiable au point a, et son dérivé à une égale Q (0).

Dans la pratique, la continuité de la différence quotient Q (h) à h = 0 est représentée en modifiant le numérateur pour annuler h dans le dénominateur. Ce processus peut être long et fastidieux pour les fonctions complexes, et de nombreux raccourcis sont couramment utilisés pour simplifier le processus.

Exemple

La fonction d'élévation au carré f (x) = x ² est différentiable en x = 3, et son dérivé est là 6. Ceci est prouvé par l'écriture du quotient de différence comme suit:

${F (3 + h) -f (3) \ over h} = {(3 + h) ^ 2-9 \ over {h}} = {9 + 6h + h ^ 2-9 \ over {h}} = {6h + h ^ 2 \ over {h}} = 6 + h.$

Alors nous obtenons la fonction simplifiée dans la limite:

$\ Lim_ {h \ 0} 6 h = + 6 + 0 = 6.$

La dernière expression montre que le quotient de différence est égale à 6 + h lorsque h ne est pas zéro et ne est pas définie lorsque h est égal à zéro. (Rappelez-vous qu'en raison de la définition du quotient de différence, le quotient de différence est toujours pas définie lorsque h est zéro.) Cependant, il est un moyen naturel de remplir une valeur pour le quotient de différence à zéro, à savoir 6. D'où la pente de la courbe de la fonction d'élévation au carré au point (3, 9) est de 6, et ainsi de son dérivé à x = 3 est f '(3) = 6.

Plus généralement, un calcul similaire montre que la dérivée de la fonction d'élévation au carré à x = est un f '(a) = 2 a.

Continuité et dérivabilité

Cette fonction ne est pas un dérivé au point marqué, que la fonction ne est pas continue là.

Si y = f (x) est dérivable en a, alors f doit également être continue à une. Par exemple, choisir un point A et soit f la fonction de l'étape qui retourne une valeur, soit 1, pour tout x moins d'un, et retourne une valeur différente, disons 10, pour tout x supérieur ou égal à un. f ne peut pas avoir un dérivé à un. Si h est négatif, alors a + h est sur la partie basse de l'étape, de sorte que la ligne à partir d'une sécante à une H + sera très raide, et lorsque h tend vers zéro, la pente tend vers l'infini. Si h est positif, alors a + h est sur la partie haute de l'étape, de sorte que la sécante d'un à un H + aura pente nulle. En conséquence, les droites sécantes ne se approchent pas de pente unique, donc ne existe pas la limite du quotient de différence.

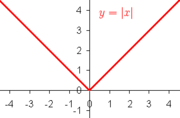
La fonction valeur absolue est continue, mais ne parvient pas à être différentiable en x = 0 car il a un angle vif.

Cependant, même si une fonction est continue en un point, il peut ne pas être différentiables il. Par exemple, la valeur absolue fonction y = | x | est continue en x = 0, mais il ne est pas différentiable il. Si h est positif, alors la pente de la droite sécante de 0 à h est un, alors que si h est négative, alors la pente de la droite sécante de 0 à h est négatif. Ceci peut être vu graphiquement comme un «coude» dans le graphique à x = 0. Même une fonction avec un graphique en douceur ne est pas différentiable en un point où sa tangente est verticale: Par exemple, la fonction y = ³ √ x ne est pas différentiable en x = 0.

La plupart des fonctions qui se produisent dans la pratique ont dérivés à tous les points ou à presque tous les points. Cependant, à la suite de Stefan Banach stipule que l'ensemble des fonctions qui ont un dérivé à un moment donné est une ensemble maigre en l'espace de toutes les fonctions continues. Officieusement, cela signifie que les fonctions différentiables sont très atypique parmi les fonctions continues. Le premier exemple connu d'une fonction qui est continue partout mais nulle part différentiable est le Fonction de Weierstrass.

Le dérivé en fonction

Soit f une fonction qui a une dérivée en tout point un dans le domaine de f. Parce que chaque point a une dérivée, il est une fonction qui envoie le point A à la dérivée de f à un. Cette fonction se écrit f '(x) et est appelé la fonction dérivée ou la dérivée de f. La dérivée de f rassemble tous les dérivés de f à tous les points dans le domaine de f.

Parfois f a une dérivée au plus, mais pas tous, les points de son domaine. La fonction dont la valeur est égale à une f '(a) si f' (a) est défini et ne est pas défini ailleurs est également appelé la dérivée de f. Il est encore une fonction, mais son domaine est strictement inférieure à la domaine de f.

En utilisant cette idée, la différenciation devient une fonction de fonctions: Le dérivé est un l'opérateur dont le domaine est l'ensemble de toutes les fonctions qui ont dérivés en tout point de leur domaine et dont la gamme est un ensemble de fonctions. Si l'on désigne par cet opérateur D, puis D (f) est la fonction f '(x). Depuis D (f) est une fonction, il peut être évalué à un point a. D'après la définition de la fonction dérivée, D (f) (a) = f '(a).

A titre de comparaison, considérer la fonction de doublement f (x) = x 2; f est une fonction à valeur réelle d'un nombre réel, ce qui signifie qu'il prend numéros comme entrées et sorties a nombres comme:

$\ Begin {align} 1 & {} \ mapsto 2, 2 \\ & {} \ mapsto 4, 3 \\ & {} \ mapsto 6. \ end {align}$

L'opérateur D, cependant, ne est pas défini sur un numéro individuel. Il est défini que sur les fonctions:

$\ Begin {align} D (x \ mapsto 1) & = (x \ mapsto 0), \\ D (x \ mapsto x) & = (x \ mapsto 1), \\ D (x \ mapsto x ^ 2) & = (x \ mapsto 2 \ cdot x). \ End {align}$

Parce que la sortie de D est une fonction dont la sortie D peut être évalué à un point. Par exemple, lorsque D est appliquée à la fonction de mise au carré,

$x \ mapsto x ^ 2,$

D envoie la fonction de doublement,

$x \ mapsto 2x,$

que nous avons nommée f (x). Cette fonction de sortie peut alors être évaluée pour obtenir f (1) = 2, f (2) = 4, et ainsi de suite.

Dérivés plus élevés

Soit f une fonction dérivable, et f '(x) son dérivé. La dérivée de f '' (x) (se il en a un) est écrit f '(x) et est appelé la dérivée seconde de f. De même, la dérivée d'une dérivée seconde, si elle existe, se écrit f '' '(x) et est appelé le troisième dérivée de f. Ces dérivés répétées sont appelés dérivés d'ordre supérieur.

Une fonction f peut être dépourvu d'un dérivé, par exemple, si elle ne est pas continue. De même, même si f a un dérivé, il peut ne pas avoir une dérivée seconde. Par exemple, laissez-

$f (x) = \ begin {} cas x ^ 2, et \ mbox {if} x \ ge 0 \\ -x ^ 2, et \ mbox {if} x \ le 0 \ end {} cas$ .

Un calcul élémentaire montre que f est une fonction dont la dérivée est différentiable

$f '(x) = \ begin {} cas 2x, et \ mbox {if} x \ ge 0 \\ -2x, & \ mbox {if} x \ le 0 \ end {} cas$ .

f '(x) est le double de la fonction valeur absolue, et il n'a pas un dérivé à zéro. Des exemples similaires montrer qu'une fonction peut avoir des dérivés de k pour tout entier k non-négatif, mais pas (k + 1) dérivé -order. Une fonction qui a des dérivées successives k est appelé k fois dérivable. Si en plus la k ième dérivée est continue, alors la fonction est dit être des différentiabilité classe C ^k. (Ce est une condition plus forte que d'avoir des dérivés de k. Pour un exemple, voir classe différentiabilité.) Une fonction qui a une infinité de dérivés est appelé indéfiniment différentiable ou lisse.

Sur la ligne réelle, chaque fonction polynomiale est infiniment différentiable. Par la norme règles de différenciation, si un polynôme de degré n est différencié n fois, alors il devient un fonction constante. Tous ses dérivés ultérieures sont identiquement nulle. En particulier, ils existent, afin polynômes sont des fonctions lisses.

Les dérivés d'une fonction f à un point x fournissent des approximations polynômes à cette fonction à proximité de x. Par exemple, si f est deux fois dérivable, puis

$f (x + h) \ env f (x) + f '(x) + h \ tfrac12 f' '(x) h ^ 2$

en ce sens que

$\ Lim_ {h \ 0} \ frac {f (x + h) - f (x) - f '(x) h - \ frac12 f' '(x) h ^ 2} {h ^ 2} = 0.$

Si f est infiniment différentiable, alors ce est le début de la série de Taylor pour f.

Notations de différenciation

Notation de Leibniz

La notation pour les produits dérivés introduits par Gottfried Leibniz est l'un des premiers. Il est encore couramment utilisée lorsque l'équation y = f (x) est considérée comme une relation fonctionnelle entre variables dépendantes et indépendantes. Ensuite, le premier dérivé est désigné par

$\ Frac {} {dy dx}, \ quad \ frac {} {df dx} (x), \; \; \ mathrm {ou} \; \; \ Frac {d} {dx} f (x).$

Dérivés plus élevés sont exprimés en utilisant la notation

$\ Frac {d ^ ny} {dx ^ n}, \ quad \ frac {d ^ nf} {dx ^ n} (x), \; \; \ mathrm {ou} \; \; \ Frac {d ^ n} {dx ^ n} f (x)$

pour la n ième dérivée de y = f (x) (par rapport à x).

Avec la notation de Leibniz, nous pouvons écrire la dérivée de y au point x = une de deux façons différentes:

$\ Frac {} {dx dy} \ left {\ \ \ frac {} {}!} \ Right |. _ {X = a} = \ frac {} {dx dy} (a).$

Notation de Leibniz permet de spécifier la variable de différenciation (dans le dénominateur). Ceci est particulièrement pertinent pour les différentiation partielle. Il rend également le règle facile à retenir de la chaîne:

$\ Frac {} {dx dy} = \ frac {} {dy du} \ cdot \ frac {du} {dx}.$

La notation de Lagrange

Un des notations modernes les plus courantes pour la différenciation est due à Joseph Louis Lagrange et utilise le Premier marque, f sorte que la dérivée d'une fonction f (x) est notée '(x) ou tout simplement f'. De même, les seconde et troisième dérivés sont désignés

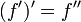$(F ')' = f '' \,$ et $(F '') '= f' '' \ ,.$

Au-delà de ce point, certains auteurs utilisent chiffres romains tels que

$f ^ {\ mathrm {iv}} \,$

pour le quatrième dérivé, alors que d'autres auteurs placent au nombre de dérivés entre parenthèses:

$f ^ {(4)} \,$

Cette dernière notation généralise pour donner le f notation ⁽ⁿ⁾ pour le n-ième dérivée de f - cette notation est très utile lorsque l'on veut parler de la dérivée comme étant une fonction elle-même, comme dans ce cas la notation Leibniz peut devenir encombrant.

La notation de Newton

La notation de Newton pour la différenciation, aussi appelée la notation par points, met un point sur le nom de la fonction de représenter un dérivé. Si y = f (t), et

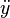
$\ Dot {y}$ et $\ Ddot {y}$

désignent, respectivement, les première et deuxième dérivées de y par rapport à t. Cette notation est utilisée presque exclusivement pour dérivées dans le temps, ce qui signifie que la variable indépendante de la fonction représente le temps . Il est très commun dans la physique et dans les disciplines mathématiques liés à la physique telles que les équations différentielles . Alors que la notation devient ingérable pour les dérivés d'ordre élevé, dans la pratique, que très peu de dérivés sont nécessaires.

La notation d'Euler

Euler notation s 'utilise une opérateur différentiel D, qui est appliqué à une fonction f pour donner le dérivé premier Df. La dérivée seconde est notée D ² f, et la n ième dérivé est désigné D ⁿ f.

Si y = f (x) est une variable dépendante, alors souvent l'indice x est fixé à la D pour clarifier la variable indépendante x. La notation d'Euler se écrit alors

$D_x y \,$ ou $D_x f (x) \,$ ,

bien que cela indice est souvent omis lorsque la variable x est compris, par exemple, lorsque ce est la seule présente variable dans l'expression.

La notation d'Euler est utile pour énoncer et résoudre équations différentielles linéaires.

Le calcul de la dérivée

La dérivée d'une fonction peut, en principe, être calculée à partir de la définition en considérant le quotient de la différence et le calcul de la limite. Pour quelques exemples, voir Dérivés (exemples). Dans la pratique, une fois que les dérivés de quelques fonctions simples sont connus, les dérivés d'autres fonctions sont plus facilement calculées en utilisant les règles d'obtention de dérivés de fonctions plus complexes à partir de plus simples.

Dérivés de fonctions élémentaires

En outre, les dérivés de certaines fonctions communes sont utiles à connaître.

Dérivés de pouvoirs: si

$f (x) = x ^ r \,$ ,

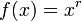où r est tout nombre réel , alors

$f '(x) = rx ^ {r-1} \,$ ,

où cette fonction est définie. Par exemple, si r = 1/2, puis

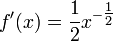$f '(x) = \ frac {1} {2} x ^ {- \ tfrac12} \,$ .

et la fonction est définie que pour x non-négative. Lorsque r = 0, cette règle récupère la règle constante.

Exponentielles et logarithmes fonctions:

$\ Frac {d} {dx} e ^ x = e ^ x$

$\ Frac {d} {} dx = a ^ x \ ln (a) a ^ x$

$\ Frac {d} {dx} \ ln (x) = 1 / x, \ qquad x> 0$

$\ Frac {d} {dx} \ log_a (x) = \ frac {1} {x \ ln (a)}$

Les fonctions trigonométriques :

$\ Frac {d} {dx} \ sin (x) = \ cos (x).$

$\ Frac {d} {dx} \ cos (x) = - \ sin (x).$

$\ Frac {d} {dx} \ tan (x) = \ s ^ 2 (x).$

Fonctions trigonométriques inverses:

$\ Frac {d} {dx} \ arcsin (x) = \ frac {1} {\ sqrt {1-x ^ 2}}.$

$\ Frac {d} {dx} \ arccos (x) = - \ frac {1} {\ sqrt {1-x ^ 2}}.$

$\ Frac {d} {dx} \ arctan (x) = \ frac {1} {{1 + x ^ 2}}.$

Règles pour trouver le dérivé

Dans de nombreux cas, les calculs compliqués de limites par l'application directe de la différence le quotient de Newton peuvent être évités en utilisant les règles de différenciation. Certaines des règles les plus élémentaires sont les suivants.

Règle constante: si f (x) est constante, alors

$f '= 0 \,$

Règle Somme:

$(Af + bg) '= af' + bg \ ',$ pour toutes les fonctions F et G et tous les nombres réels a et b.

règle de produit:

$(Fg) '= f' g + fg \ ',$ pour toutes les fonctions f et g.

Quotient règle:

$\ Left (\ frac {f} {g} \ right) '= \ frac {f'g - fg'} {g ^ 2}$

règle de la chaîne: Si $f (x) = h (g (x))$ , Puis

$f '(x) = h' (g (x)) g '(x) \,$ .

Exemple de calcul

Le dérivé de

$f (x) = x ^ 4 + \ sin (x ^ 2) - \ ln (x) e ^ x + 7 \,$

est

$\ Begin {align} f '(x) = & 4 x ^ {(4-1)} + \ frac {d \ gauche (x ^ 2 \ right)} {dx} \ cos (x ^ 2) - \ frac {d \ gauche (\ ln {x} \ right)} {dx} e ^ x - \ ln {x} \ frac {d \ gauche (e ^ x \ right)} {dx} + 0 = \\ & 4x ^ 3 + 2x \ cos (x ^ 2) - \ ln (x) e ^ x - de frac {1} {x} e ^ x \. \ End {align}$

Voici le second terme a été calculé en utilisant la règle de la chaîne et la troisième en utilisant la règle du produit: les dérivés connus des fonctions élémentaires x ², x ^4, sin (x), ln (x) et exp (x) = e ^x ont également été utilisés .

Dérivés de dimensions supérieures

Dérivés de fonctions vectorielles valeur

Un valeurs vectorielles fonction y (t) d'une variable réelle est une fonction qui envoie des nombres réels à des vecteurs dans certains espace vectoriel R ^n. Une fonction de vecteur à valeur peut être subdivisée en ses fonctions de coordonnées y ₁ (t), y ₂ (t), ..., y _n (t), ce qui signifie que y (t) = (y ₁ (t), ... , y _n (t)). Cela comprend, par exemple, courbes paramétriques par R ² ou R ^3. Les fonctions coordonnées sont réelles fonctions évaluées, de sorte que la définition ci-dessus de dérivé se applique à eux. La dérivée de y (t) est défini comme étant le vecteur , appelé le vecteur tangent, dont les coordonnées sont les dérivées des fonctions de coordonnées. C'est,

$\ Mathbf {y} '(t) = (y'_1 (t), \ ldots, y'_n (t)).$

De manière équivalente,

$\ Mathbf {y} '(t) = \ lim_ {h \ 0} \ frac {\ mathbf {y} (t + h) - \ mathbf {y} (t)} {h},$

si la limite existe. La soustraction dans le numérateur est la soustraction de vecteurs, et non scalaires. Si la dérivée de y existe pour chaque valeur de t, alors y 'est une autre fonction de valeurs vectorielles.

Si e _1, ..., e _n est la norme de base pour R ^n, y (t) peut aussi se écrire comme y ₁ (t) e ₁ + ... + y _n (t) e _n. Si nous supposons que la dérivée d'une fonction vectorielle évalués conservent la propriété de linéarité, la dérivée de y (t) doit être

$y'_1 (t) \ mathbf {e} _1 + \ cdots + y'_n (t) \ mathbf {e} _n$

parce que chacun des vecteurs de base est une constante.

Cette généralisation est utile, par exemple, si y (t) est le vecteur de position d'une particule à l'instant t; alors le dérivé de y '(t) est la vitesse de la particule vecteur à l'instant t.

Dérivées partielles

Supposons que f est une fonction qui dépend de plus d'une variable. Par exemple,

$f (x, y) = x ^ 2 + xy + y ^ 2. \,$

f peut être réinterprété comme une famille de fonctions d'une variable indexé par les autres variables:

$f (x, y) = f_x (y) = x ^ 2 + xy + y ^ 2. \,$

En d'autres termes, à chaque valeur de x choisit une fonction notée f _x, qui est une fonction d'un nombre réel. C'est,

$x \ mapsto f_x, \,$

$f_x (y) = x ^ 2 + xy + y ^ 2. \,$

Une fois qu'une valeur de x est choisi, par exemple un, alors f (x, y) détermine une fonction f qui y envoie _un à un ² + ay + y ²:

$f_a (y) = a ^ ay + 2 + y ^ 2. \,$

Dans cette expression, a est un, pas une variable constante, de sorte que f _a est _une fonction d'une seule variable réelle. Par conséquent, la définition de la dérivée d'une fonction d'une variable se applique:

$f_a '(y) = a + 2y. \,$

La procédure ci-dessus peut être réalisée pour ne importe quel choix d'un. Assemblage des dérivés, ainsi que dans une fonction donne une fonction qui décrit la variation de f dans la direction y:

$\ Frac {\ part f} {\ part y} (x, y) = x + 2y.$

Ce est la dérivée partielle de f par rapport à y. Voici ∂ est une d arrondi appelé le symbole dérivée partielle. Pour le distinguer de la lettre d, ∂ est parfois prononcé "der", "del", ou "partielle" au lieu de "dee".

En général, la dérivée partielle d'une fonction f (x _1, ..., x _n) dans la direction x _i au point (a ₁ ..., a _n) est défini comme étant:

$\ Frac {\ part f} {\ part x_i} (a_1, \ ldots, a_n) = \ lim_ {h \ 0} \ frac {f (a_1, \ ldots, a_i + h, \ ldots, A_N) - f (a_1, \ ldots, a_n)} {} h.$

Dans la différence quotient ci-dessus, toutes les variables, sauf x _i sont maintenus fixes. Ce choix de valeurs fixes détermine une fonction d'une variable

$F_ {a_1, \ ldots, a_ {i-1}, {a_ i + 1}, \ ldots, a_n} (x_i) = f (A_1, \ ldots, a_ {i-1}, x_i, a_ {i + 1}, \ ldots, a_n)$

et, par définition,

$\ Frac {{df_ A_1, \ ldots, a_ {i-1}, {a_ i + 1}, \ ldots, a_n}} {} dx_i (a_1, \ ldots, a_n) = \ frac {\ part f} { \ part x_i} (a_1, \ ldots, A_N).$

En d'autres termes, les différents choix d'un indice d'une famille de fonctions à une variable de même que dans l'exemple ci-dessus. Cette expression montre également que le calcul des dérivées partielles réduit pour le calcul des dérivés à une variable.

Un exemple important d'une fonction de plusieurs variables est le cas d'un fonction f de scalaires (x _1, ... x _n) sur un domaine dans l'espace euclidien R ⁿ (par exemple, le R ou R ² ³). Dans ce cas f a une dérivée partielle ∂ f / ∂ _{x j} par rapport à chaque variable x _j. Au point a, ces dérivées partielles définissent le vecteur

$\ Nabla f (a) = \ left (\ frac {\ f partielle} {\ x_1 partielle} (a), \ ldots, \ frac {\ f partielle} {\ de x_n partielle} (a) \ right).$

Ce vecteur est appelé le gradient de f en un. Si f est dérivable en tout point dans certains domaine, le gradient est une fonction ∇ vecteur f-valeur qui prend le point a au vecteur ∇ f (a). En conséquence, le gradient détermine une champ de vecteurs.

Dérivées directionnelles

Si f est une fonction à valeurs réelles sur R ^n, alors les dérivées partielles de f mesure la variation dans la direction des axes de coordonnées. Par exemple, si f est une fonction de x et y, puis ses dérivées partielles mesurent la variation de f dans la direction x et la direction y. Ils ne ont pas, cependant, de mesurer directement la variation de f dans une autre direction, comme le long de la ligne y diagonales = x. Ils sont évalués en utilisant des dérivés directionnelles. Choisissez un vecteur

$\ Mathbf {v} = (v_1, \ ldots, V_n).$

La dérivée directionnelle de f dans la direction de v au point x est la limite

$D _ {\ mathbf {v}} {f} (\ boldsymbol {x}) = \ lim_ {h \ rightarrow 0} {\ frac {f (\ boldsymbol {x} + h \ mathbf {v}) - f (\ boldsymbol {x})} {h}}.$

Soit λ être un scalaire. La substitution de h / λ pour h change différence le quotient de λ v direction dans les temps λ différence de quotient de la direction de v. Par conséquent, la dérivée directionnelle dans la direction de λ c λ est la fois dérivée directionnelle dans la direction de v. Pour cette raison, dérivées directionnelles sont souvent considérés uniquement pour les vecteurs unitaires c.

Si toutes les dérivées partielles de f existent et sont continues en x, puis ils déterminent la dérivée directionnelle de f dans la direction v par la formule:

$D _ {\ mathbf {v}} {f} (\ boldsymbol {x}) = \ sum_ {j = 1} ^ n v_j \ frac {\ f partielle} {\ x_j partielle}.$

Ceci est une conséquence de la définition de la dérivée totale. Il se ensuit que la dérivée directionnelle est linéaire dans v.

La même définition fonctionne également lorsque f est une fonction à valeurs dans R ^m. On utilise simplement la définition ci-dessus dans chacune des composantes des vecteurs. Dans ce cas, la dérivée directionnelle est un vecteur de R ^m.

La dérivée totale, l'écart total et le jacobien

Soit f une fonction à partir d'un domaine dans R à R. La dérivée de f en un point a dans son domaine est la meilleure approximation linéaire à f à ce point. Comme ci-dessus, ce est un nombre. Géométriquement, si v est un vecteur d'unité en commençant à un, alors f '(a), la meilleure approximation linéaire de f en a, doit être la longueur du vecteur v trouvé en déplaçant vers l'espace cible à l'aide f. (Ce vecteur est appelé pushforward de v par f et est habituellement écrite $f_ * v$ .) En d'autres termes, si v est mesurée en termes de distances sur la cible, alors, parce que v ne peut être mesurée par f, v ne semble plus être un vecteur de l'unité parce f ne préserve pas des vecteurs unitaires. Au lieu de cela semble avoir v longueur f '(a). Si m est supérieur à un, puis en écrivant f en utilisant des fonctions de coordonnées, la longueur de v dans chacune des directions de coordonnées peut être mesurée séparément.

Supposons maintenant que f est une fonction d'un domaine à R ⁿ à ^m et que R a est un point dans le domaine de f. La dérivée de f à une devrait toujours être la meilleure approximation linéaire pour f à un. En d'autres termes, si v est un vecteur de R ^n, f '(a) doit être le transformation linéaire qui approxime le mieux f. La transformation linéaire doit contenir toutes les informations sur la façon f transforme vecteurs à un des vecteurs à f (a), et en symboles, ce qui signifie qu'il devrait être la transformation linéaire f '(a) de telle sorte que

$\ {Lim_ || \ mathbf {h} || \ rightarrow 0} \ frac {|| f (\ mathbf {a} + \ mathbf {h}) - f (\ mathbf {a}) - f '(\ mathbf {a}) \ mathbf {h}} {|| || \ mathbf {h}} || = 0.$

Voici h est un vecteur de R ^n, de sorte que le norme dans le dénominateur est la longueur standard sur R ^n. Cependant, f '(a) h est un vecteur de R ^m, et la norme dans le numérateur est la longueur standard sur R ^m. La transformation linéaire f '(a), se il existe, est appelée la dérivée totale de f à un ou le (s) différentielle de f en a.

Si la dérivée totale existe à un, tous les dérivées partielles de f existent à un. Si l'on écrit f en utilisant des fonctions de coordonnées, de sorte que f = (f _1, f _2, ..., f _m), la dérivée totale peut être exprimé comme une matrice appelée Matrice jacobienne de f en un:

$f '(\ mathbf {a}) = \ text {} Jac _ {\ mathbf {a}} = \ left (\ frac {\ f_i partielle} {\ x_j partielle} \ right) _ {} ij.$

L'existence de la jacobienne est strictement plus forte que l'existence de toutes les dérivées partielles, mais si les dérivées partielles existent et satisfont à des conditions de régularité doux, alors la dérivée totale existe et est donné par la jacobienne.

La définition de la dérivée totale englobe la définition de la dérivée dans une variable. Dans ce cas, le dérivé totale existe si et seulement si le dérivé d'habitude existe. La matrice jacobienne est réduite à une matrice 1 × 1 dont l'entrée est uniquement la dérivée f '(x). Cette matrice 1 × 1 satisfait la propriété que f (a + h) - f (a) - f '(a) h est approximativement nulle, en d'autres termes que

$f (a + h) \ env f (a) + f '(a) h.$

Jusqu'à des variables changeantes, ce est la déclaration que la fonction 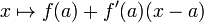$x \ mapsto f (a) + f '(a) (x-a)$ est la meilleure approximation linéaire de f à un.

Le dérivé d'une fonction totale ne donne pas une autre fonction de la même façon que des cas une variable. Ce est parce que la dérivée totale d'une fonction multivariée doit enregistrer beaucoup plus d'informations que la dérivée d'une fonction à une seule variable. Au lieu de cela, le dérivé totale donne une fonction de la faisceau tangent à la source de faisceau de la tangente de la cible.

Généralisations

Le concept d'un dérivé peut être étendu à bien d'autres paramètres. Le dénominateur commun est que la dérivée d'une fonction en un point sert de approximation linéaire de la fonction à ce moment.

Une généralisation des préoccupations importantes dérivés complexes des fonctions de variables complexes, telles que les fonctions de (dans un domaine) le nombres complexes C à C. La notion de la dérivée d'une telle fonction est obtenue en remplaçant les variables réelles avec des variables complexes dans la définition. Cependant, cette définition innocente se cache des propriétés très profondes. Si C est identifié avec R ² en attribuant un nombre complexe z comme x + y i, puis une fonction différentiable de C à C est certainement différentiable en fonction de R à R ² ² (en ce sens que ses dérivées partielles existent tous) , mais l'inverse ne est pas vrai en général: le dérivé complexe ne existe que si le dérivé réel est linéaire complexe et cela impose des relations entre les dérivées partielles appelé Équations de Cauchy Riemann - voir fonctions holomorphes.

Un autre concerne la généralisation fonctions entre variétés différentiables ou lisses. Intuitivement parle une telle variété M est un espace qui peut être approchée à proximité de chaque point x par un espace vectoriel appelé son espace tangente: l'exemple prototypique est un surface lisse en R ³. Le dérivé (ou différentiel) d'un (différentiables) f: M → N entre les collecteurs, à un point x dans M, est alors une linéaire de l'espace tangent de M en x à l'espace tangent de N à f (x). La fonction dérivée devient une carte entre le tangents faisceaux de m et n. Cette définition est fondamentale dans la géométrie différentielle et a de nombreuses utilisations - voir pushforward (différentiel) et recul (géométrie différentielle).

Différenciation peut également être définie pour les cartes entre dimension infinie espaces vectoriels tels que Espaces de Banach et Espaces de Fréchet. Il est à la fois une généralisation de la dérivée directionnelle, appelée Gâteaux dérivé, et de l'écart, appelé le Fréchet.

Un déficit du dérivé classique est que pas beaucoup de fonctions sont différentiables. Néanmoins, il existe un moyen d'étendre la notion de la dérivée de sorte que toutes des fonctions continues et de nombreuses autres fonctions peuvent être différenciées en utilisant un concept connu sous le nom dérivée faible. L'idée est d'intégrer les fonctions continues dans un espace plus large appelé l'espace de distributions et ne nécessitent qu'une fonction est différentiable "en moyenne".

Les propriétés du dérivé ont inspiré l'introduction et l'étude de nombreux objets similaires en algèbre et topologie - voir, par exemple, algèbre différentielle.

Récupéré à partir de " http://en.wikipedia.org/w/index.php?title=Derivative&oldid=198886698"