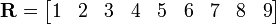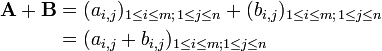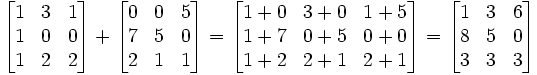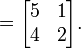Matrix (mathématiques)

Contexte des écoles Wikipédia

SOS Enfants a essayé de rendre le contenu plus accessible Wikipedia par cette sélection des écoles. Avant de vous décider à propos de parrainer un enfant, pourquoi ne pas en apprendre davantage sur différents organismes de parrainage premier ?

En mathématiques , une matrice (matrices pluriel) est une table rectangulaire d'éléments (ou entrées), qui peut être le nombre ou, plus généralement, toute quantités abstraites qui peuvent être ajoutés et multipliées. Matrices sont utilisés pour décrire des équations linéaires , de garder trace de la les coefficients de transformations linéaires et d'enregistrer les données qui dépendent de multiples paramètres. Les matrices sont décrites par le domaine de la théorie de la matrice . Les matrices peuvent être ajoutées, se multiplient, et décomposés de différentes façons, ce qui les rend aussi un concept clé dans le domaine de l'algèbre linéaire .

Dans cet article, les entrées d'une matrice sont réels ou complexes numéros, sauf indication contraire.

Organisation d'une matrice

Définitions et notations

Les lignes horizontales dans une matrice sont appelés lignes et les lignes verticales sont appelées colonnes. Une matrice à m lignes et n colonnes est appelée une matrice m -by- n (écrit m × n) et m et n sont appelés ses dimensions. Les dimensions de la matrice sont toujours données avec le premier nombre de rangées, le nombre de colonnes. Il est communément dit qu'un m -by- n matrice a un ordre de m × n («ordre» de taille signifie). Deux matrices du même ordre dont les entrées correspondant sont équivalents sont considérés comme égaux.

Presque toujours des majuscules indiquent matrices avec les lettres correspondantes avec deux indices représentant les entrées minuscules. Par exemple, l'entrée d'une matrice A qui se trouve dans la rangée i ème et j ème colonne est écrit comme un _{i, j} et appelé i, l'entrée j ou (i, j) ième entrée de A. Notations alternatifs pour que l'entrée sont A [i, j] ou A _{i, j.} La ligne est toujours noté d'abord, puis la colonne. Dans cet exemple, A (sans indices) serait symboliser toute la matrice. En plus d'utiliser les lettres majuscules comme des symboles représentant des matrices, de nombreux auteurs utilisent un style typographique spéciale, communément gras verticale (non italique), pour mieux distinguer les matrices d'autres variables. Suite à cette convention, A est une matrice, qui se distingue de A, un scalaire. Une convention alternative consiste à annoter matrices avec leurs dimensions en petits caractères sous le symbole, par exemple, $\ r \ underset {c} fois {A}$ pour la matrice d'un c r.

Nous écrivons souvent $\ Mathbf {A}: = (a_ {i, j}) _ {i = 1, \ ldots, m; \, \, j = 1, \ ldots, n}$ ou $\ Mathbf {A}: = (a_ {i, j}) _ {m \ times n}$ à définir une matrice m × n A. Dans ce cas, les entrées a _{i, j} sont définies séparément pour tous les entiers 1 ≤ i ≤ m et 1 ≤ j ≤ n. Dans certains langages de programmation, la numérotation des lignes et des colonnes à partir de zéro. Textes qui utilisent une telle langue largement, suivez fréquemment cette convention, nous avons donc 0 ≤ i ≤ m -1 et 0 ≤ j ≤ n -1.

Une matrice où l'une des dimensions un égale est souvent appelé un vecteur, et interprétée comme un élément de l'espace réel coordonner . Une matrice m × 1 (une colonne et m lignes) est appelé vecteur de colonne et une matrice n × 1 (une ligne et n colonnes) est appelé vecteur ligne.

Définition mathématique

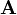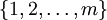Une $\, M \ times n \, \, (m, n \ in \ mathbb {N})$ matrice $\ Mathbf {A} \,$ est une fonction $\ Mathbf {A} \ colon \ {1, 2, \ ldots, m \} \ times \ {1, 2, \ ldots, n \} \ à \ mathbf {S}, \, \,$ où $\ Mathbf {S} \,$ est toute non- ensemble vide.

$(\ {1, 2, \ ldots, m \} \ times \ {1, 2, \ ldots, n \} \,$ est le Produit cartésien d'ensembles $\ {1, 2, \ ldots, m \} \,$ et $\ {1, 2, \ ldots, n \}.) \,$

Nous disons que la matrice $\ Mathbf {A}$ est une matrice sur l'ensemble $\ Mathbf {S}$ . La chose importante à noter est que, si nous voulons avoir algèbre matricielle, l'ensemble $\ Mathbf {S} \,$ doit être un anneau et la matrice $\ Mathbf {A}$ doit être une matrice carrée (voir matrices carrées et définitions connexes ci-dessous pour plus d'explications). Depuis l'ensemble des matrices carrées sur un anneau est aussi un anneau, algèbre matricielle est généralement appelé anneau de matrice.

Depuis que cet article considère principalement matrices sur des nombres réels , matrices présentés ici sont en fait des fonctions $\ Mathbf {A} \ colon \ {1, 2, \ ldots, m \} \ times \ {1, 2, \ ldots, n \} \ \ mathbb à {R}. \, \,$

Exemple

La matrice

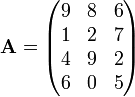
$\ Mathbf {A} = \ begin {} bmatrix 9 & 8 & 6 \\ 1 & 2 & 7 \\ 4 & 9 & 2 \\ & 6 & 5 0 \ end {} bmatrix$ ou $\ Mathbf {A} = \ begin {} pmatrix 9 & 8 & 6 \\ 1 & 2 & 7 \\ 4 & 9 & 2 \\ & 6 & 5 0 \ end {} pmatrix$

est un $4 \ times 3$ matrice. Elément $a_ {2,3}$ ou $\ Mathbf {A} [2,3]$ est 7. En termes de la définition mathématique donnée ci-dessus, cette matrice est une fonction $\ Mathbf {A} \ colon \ {1, 2, 3, 4 \} \ times \ {1, 2, 3 \} \ à \ mathbb {R} \,$ et, par exemple, $\ Mathbf {A} ((2, 3)) = 7 \,$ et $\ Mathbf {A} ((3, 1)) = 4. \,$

La matrice

$\ Mathbf {R} = \ begin {} bmatrix 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 \ end {} bmatrix$

est un $1 \ 9 fois$ matrice, ou 9-élément de vecteur ligne.

Additionner et multiplier des matrices

Somme

Deux ou plusieurs matrices de dimensions identiques m et n peuvent être ajoutés. M -by- n matrices donnée A et B, leur somme A + B est la matrice m -by- n calculée en ajoutant des éléments correspondants:

$\ Begin {align} \ mathbf {A} + \ mathbf {B} & = (a_ {i, j}) _ {1 \ le i \ le m; \, 1 \ le j \ le n} + (b_ { i, j}) _ {1 \ le i \ le m; \, 1 \ le j \ le n} \\ & = (a_ {i, j} + b_ {i, j}) _ {1 \ le i \ le m; 1 \ le j \ le n} \\ \ end {align}$

Par exemple:

$\ Begin {} bmatrix 1 & 3 & 1 \\ 1 & 0 & 0 \\ 1 & 2 & 2 \ end {} bmatrix + \ begin {} bmatrix 0 & 0 et 5 \\ 7 & 5 & 0 \\ 2 & 1 & 1 \ end {} bmatrix = \ begin {} bmatrix 1 + 0 et 3 + 0 + 1 et 5 \\ 1 + 7 + 5 & 0 & 0 + 0 \\ 1 + 2 et 2 + 1 & 2 1 \ end {} bmatrix = \ begin {} bmatrix 1 & 3 & 6 \\ 8 & 5 & 0 \\ 3 & 3 & 3 \ end {} bmatrix$

Un autre, notion beaucoup moins souvent utilisé de l'addition de la matrice est la somme directe.

Multiplication scalaire

Etant donné une matrice A et un nombre c, la multiplication scalaire c A est obtenu en multipliant chaque élément de A par la c scalaire (ce est à dire $(C \ mathbf {A}) _ {i, j} = c \ cdot a_ {i, j}$ ). Par exemple:

$2 \ cdot \ begin {} bmatrix 1 & 8 & -3 \\ & 4 & 5 -2 \ end {} bmatrix = \ begin {} bmatrix 2 \ cdot 1 & 2 \ cdot 8 & 2 \ cdot -3 \\ 2 \ cdot 4 & 2 \ cdot -2 et 2 \ cdot 5 \ end {} bmatrix = \ begin {} bmatrix 2 & 16 & 8 -6 \\ & -4 et 10 \ end {} bmatrix$

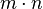plus de Matrix et la multiplication scalaire tourner l'ensemble $\ Text {M} (m, n, \ mathbb {R})$ de tout $m$ -by- $n$ matrices avec de vraies entrées dans un véritable espace vectoriel de dimension $m \ cdot n$ .

La multiplication de matrices

La multiplication de deux matrices est bien définie que si le nombre de colonnes de la matrice de gauche est la même que le nombre de lignes de la matrice droite. Le point du milieu ( $\ Cdot$ ) Ne est pas utilisé pour indiquer la multiplication matricielle (il est utilisé pour la multiplication scalaire). Si A est une matrice m -by- n et B n est une matrice p -by-, puis leur produit matriciel AB est la matrice m -by- p donné par:

$(\ Mathbf {AB}) _ {i, j} = a_ {i, 1} b_ {1, j} + a_ {i, 2} b_ {2, j} + \ ldots + a_ {i, n} b_ {n, j}$

pour chaque paire 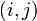$(I, j)$ . Par exemple:

$\ Begin {} bmatrix 1 & 0 & 2 -1 \\ & 3 & 1 \\ \ end {bmatrix} \ times \ begin {} bmatrix 3 & 1 \\ 2 & 1 \\ 1 & 0 \\ \ end { bmatrix} = \ begin {} bmatrix (1 \ times 3 + 0 \ times 2 + 2 \ times 1) & (1 \ times 1 + 0 \ times 1 + 2 \ times 0) \\ (-1 \ fois 3 + 3 \ times 2 + 1 \ times 1) & (-1 \ fois 1 + 3 \ times 1 + 1 \ times 0) \\ \ end {} bmatrix$

$= \ Begin {} bmatrix 5 & 1 \\ 4 & 2 \\ \ end {} bmatrix.$

La multiplication de matrices a les propriétés suivantes:

(AB) C = A (BC) pour le m de tous les k matrices A, m -by- n matrices B et n -by- p matrices C («associativité»).
(A + B) C = AC + BC pour tout m -by- n matrices A et B et n -by- k matrices C ("distributivité droit»).
C (A + B) = CA + CB pour tout m -by- n matrices A et B et K matrices -by- m C ("distributivité à gauche»).

La multiplication de matrices ne est pas commutative ; qui est, étant donné matrices A et B et leur produit défini, alors généralement AB $\ Ne$ BA. Il peut également arriver que AB est défini, mais BA ne est pas défini.

En plus de la multiplication de matrice ordinaire vient d'être décrite, il existe d'autres opérations sur des matrices qui peuvent être considérés formes de multiplication, comme le produit de Hadamard et la Produit de Kronecker.

Transformations linéaires, classe et de les transposer

Matrices peuvent représenter commodément transformations linéaires, car la multiplication de matrices correspond parfaitement à la composition de cartes, comme on le décrit ci-après. Cette même propriété en fait des structures de données puissants langages de programmation de haut niveau.

Ici et dans la suite nous identifions R ⁿ avec l'ensemble des "colonnes" ou n-1 -par matrices. Pour chaque application linéaire f: R ⁿ → R ^m il existe une m uniques -by- n matrice A tel que f (x) = Ax pour tout x dans R ^n. Nous disons que la matrice A "représente" l'application linéaire f. Maintenant, si m matrice B du k représente une autre application linéaire g: R → R ^{m k,} alors l'application linéaire g o f est représentée par BA. Cela résulte de l'associativité mentionné ci-dessus de la multiplication matricielle.

Plus généralement, une application linéaire d'un espace vectoriel de dimension n pour un m espace vectoriel de dimension est représentée par une matrice m -by- n, à condition que bases ont été choisis pour chacun.

Le rang d'une matrice A est le dimension de la image de la carte linéaire représenté par A; ce est la même que la dimension de l'espace engendré par les lignes de A, et également la même que la dimension de l'espace engendré par les colonnes de A. Il peut également être défini sans référence à l'algèbre linéaire comme suit: le rang d'un m -by- n matrice A est le plus petit nombre k tel que A peut être écrit comme un produit Colombie-Britannique où B est un m -by- de matrice de k et C est un k de la matrice n (bien que ce ne est pas un moyen pratique de calculer le rang).

Le transposition d'une matrice m -by- n n A est la matrice A m -by- ^tr (parfois aussi écrit comme un ^T ou ^t A) formé en tournant rangées en colonnes et rangées en colonnes, à savoir une ^tr [i, j] = A [j, i] pour tous les indices i et j. Si A décrit un plan linéaire par rapport à deux bases, la matrice A ^tr décrit la transposée de la carte linéaire par rapport aux bases duales, voir espace dual.

Nous avons (A + B) ^tr = A + B ^{tr tr} et (AB) = B ^{tr tr} Un ^tr.

Matrices carrées et définitions connexes

Une matrice est une matrice carrée qui a le même nombre de lignes et de colonnes. L'ensemble de tous les carrés -by- n n matrices, avec addition de la matrice et la multiplication matricielle est une anneau. Sauf n = 1, cette bague ne est pas commutative .

M (n, R), l'anneau de véritables matrices carrées, est un véritable unitaire algèbre associative. M (n, C), l'anneau de matrices complexes carrés, est une algèbre associative complexe.

La matrice unitaire ou matrice identité I _n, avec des éléments sur le principale ensemble diagonal à 1 et tous les autres éléments mis à 0, satisfait MI _n = M et je _{n N} = N pour tout m -by- n matrice M et n -by- k matrice N. Par exemple, si n = 3:

$\ Mathbf {I} _3 = \ begin {} bmatrix 1 & 0 & 0 \\ 0 & 1 & 0 0 \\ & 0 & 1 \ end {} bmatrix.$

La matrice d'identité est l'élément de l'identité dans l'anneau des matrices carrées.

Éléments inversible dans cet anneau sont appelés matrices inversibles ou matrices non singulières. Une matrice n par n A est inversible si et seulement si il existe une matrice B de telle sorte que

AB = I _n (= BA).

Dans ce cas, B est le matrice inverse de A, noté A ^-1. L'ensemble de tous les n -by- n matrices inversibles forme un groupe (en particulier un groupe de Lie) sous la multiplication de matrices, le groupe linéaire.

Si λ est un nombre et v est un vecteur non nul de telle sorte que Av = λ v, puis nous appelons v un vecteur propre de A et λ l'associé valeur propre . (Eigen signifie «propre» en allemand et en néerlandais .) Le nombre λ est une valeur propre de A si et seulement si A -λ I _n est pas inversible, ce qui arrive si et seulement si p _A (λ) = 0. Voici p _A (x) est la polynôme caractéristique de A. Ce est un polynôme de degré n et a donc n racines complexes (comptage des racines multiples en fonction de leur multiplicité). En ce sens, chaque matrice carrée a n valeurs propres complexes.

Le déterminant d'une matrice carrée A est le produit de ses n valeurs propres, mais il peut également être définie par la Formule de Leibniz. Matrices inversibles sont précisément ces matrices avec un déterminant différent de zéro.

L' élimination de Gauss algorithme est d'une importance centrale: il peut être utilisé pour calculer les déterminants, les grades et les inverses de matrices et de résoudre des systèmes d'équations linéaires .

Le trace d'une matrice carrée est la somme de ses entrées en diagonale, ce qui équivaut à la somme de ses valeurs propres n.

Matrice exponentielle est définie pour les matrices carrées, en utilisant la série de puissance .

Types de matrices spéciales

Dans de nombreux domaines des mathématiques, des matrices avec certaine structure se posent. Quelques exemples sont importants

Matrices symétriques sont telles que les éléments symétriques sur la diagonale principale (à partir du coin supérieur gauche au coin inférieur droit) sont égales, ce est-à $a_ {i, j} = {a_ j, i} \ leftrightarrow \ mathbf {A} ^ \ mathrm {T} = \ mathbf {A}$ .
Antisymétrique de telle sorte que les matrices sont symétriques autour des éléments de la diagonale principale sont le négatif de l'autre, ce est-à $a_ {i, j} = - a_ {j, i} \ leftrightarrow \ mathbf {A} ^ \ mathrm {T} = - \ mathbf {A}$ . Dans une matrice antisymétrique, tous les éléments diagonaux sont égaux à zéro, ce est-à 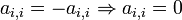$a_ {i, i} = - a_ {i, i} \ Rightarrow a_ {i, i = 0}$ .
Hermitiques (ou auto-adjoint) matrices sont telles que les éléments symétriques autour de la diagonale sont les uns des autres conjugués complexes, ce est- $a_ {i, j} = \ overline {a} {_ j, i} \ leftrightarrow \ mathbf {A} ^ \ mathrm {H} = \ mathbf {A}$ Où $\ Overline {z}$ signifie le conjugué complexe d'un nombre complexe $z$ et $\, \! \ Mathbf {A} ^ \ mathrm {H}$ la conjugué transposée de A.
Matrices de Toeplitz ont des éléments communs sur leurs diagonales, ce est- $\, \! a_ {i, j} = a_ {i + 1, j + 1}$ .
Matrices stochastiques sont des matrices carrées dont les lignes sont des vecteurs de probabilité; ils sont utilisés pour définir Chaînes de Markov.
Une matrice carrée A est appelé idempotent si $\ Mathbf {A} ^ 2 = \ mathbf {AA} = \ mathbf {A}$ .

Pour une liste plus complète voir liste des matrices.

Matrices dans l'algèbre abstraite

Si nous commençons avec un anneau R, on peut considérer l'ensemble M (m, n, R) de tous m par n matrices avec entrées dans R. L'addition et la multiplication de ces matrices peuvent être définis comme dans le cas des matrices réelles ou complexes (voir ci-dessus ). L'ensemble M (n, R) de tous les n carrée de n matrices plus R est un anneau dans son propre droit, isomorphe au anneau de endomorphisme de la gauche R - Module R ^n.

De même, si les données sont extraites d'un semiring S, plus de la matrice et la multiplication peuvent encore être définis comme d'habitude. L'ensemble de tous les n carré × n matrices sur S est elle-même un semi-anneau. Notez que les algorithmes de multiplication rapide de la matrice comme le Strassen algorithme général se appliquent uniquement aux matrices sur des anneaux et ne fonctionnera pas pour les matrices sur semi-anneaux qui ne sont pas des anneaux.

Si R est un anneau commutatif , alors M (n, R) est un Etat unitaire algèbre associative sur R. Il est alors également significative pour définir le facteur déterminant des matrices carrées en utilisant le Formule de Leibniz; une matrice est inversible si et seulement si son déterminant est inversible dans R.

Toutes les déclarations mentionnées dans cet article pour les matrices réelles ou complexes restent corrects pour les matrices sur un arbitraire domaine.

Les matrices sur une anneau de polynômes sont importants dans l'étude de la théorie du contrôle .

Matrices sans entrées

Une question subtile qui est rarement posée est de savoir si il ya une telle chose comme une matrice 3 par 0. Ce serait une matrice avec 3 rangées, mais sans colonnes, ce qui semble absurde. Toutefois, si l'on veut être en mesure d'avoir des matrices pour toutes les cartes linéaires entre espaces vectoriels de dimension finie, on a besoin de telles matrices, car il n'y a rien de mal avec des cartes linéaires d'un espace de dimension 0 à un espace à 3 dimensions (en fait, si les espaces sont fixés il ya une telle carte, la carte zéro). Donc, on est conduit à admettre qu'il ya exactement un 3-par-0 matrice (qui a 3 × 0 = 0 entrées; entrées non NULL, mais pas du tout). De même, il existe des matrices ayant un nombre de colonnes positives mais aucune ligne. En outre, même en l'absence d'entrées, il faut toujours garder une trace du nombre de lignes et de colonnes, puisque le produit BC où B est la matrice 3 par 0 et C est une matrice 0-en-4 est un tout à fait normal 3 -par-4 matrice, dont tous les 12 entrées sont 0 (comme ils sont donnés par un somme vide). Notez que ce calcul de la Colombie-Britannique justifie le critère donné ci-dessus pour le rang d'une matrice en termes d'expressions possibles comme un produit: la matrice 3-en-4 avec zéro entrées a certainement rang 0, il devrait donc être le produit d'un 3 -par 0-matrice et d'une matrice 0-en-4. Pour permettre et de distinguer entre les matrices sans entrées, matrices devraient formellement être définis, dans un style d'informatique un peu pédant, comme quadruples (A, R, C, M), où A est l'ensemble dans lequel les entrées vivent, R et C sont (naturelles) les numéros de lignes et de colonnes, et M est la collection rectangulaire d'éléments rc de A (la matrice dans le sens habituel).

Histoire

L'étude de matrices est assez vieux. Un 3-en-3 carré magique apparaît dans Littérature chinoise datant de dès 650 av.

Matrices ont une longue histoire d'application dans la résolution des équations linéaires . Un important Texte chinois d'entre 300 avant JC et 200 après JC, Les Neuf Chapitres sur l'art mathématique (Jiu Zhang Suan Shu), est le premier exemple de l'utilisation de méthodes matricielles pour résoudre des équations simultanées . Dans le septième chapitre, "Trop et pas assez," le concept d'un facteur déterminant apparaît d'abord près de 2000 ans avant sa publication par le Mathématicien japonais Seki Kowa en 1683 et le mathématicien allemand Gottfried Leibniz dans 1693.

Les carrés magiques étaient connus Mathématiciens arabes, peut-être dès le 7ème siècle, quand les Arabes ont conquis nord-ouest du Sous-continent indien et appris les mathématiques indiennes et astronomie, y compris d'autres aspects de mathématiques combinatoires . Il a également été suggéré que l'idée est venue par la Chine. Les premiers carrés magiques d'ordre 5 et 6 apparaissent dans une encyclopédie de Bagdad vers 983 AD, le Encyclopédie des Frères de la Pureté (Rasa'il Ihkwan al-Safa); simples carrés magiques ont été connus à plusieurs mathématiciens arabes antérieures.

Après le développement de la théorie des déterminants par Kowa Seki et Leibniz à la fin du 17ème siècle, Cramer a développé la théorie plus loin dans le 18e siècle, présentant La règle de Cramer en 1750 . Carl Friedrich Gauss et Wilhelm Jordan développé Gauss-Jordan élimination dans les années 1800.

Le terme «matrice» a été inventé en 1848 par JJ Sylvester. Cayley, Hamilton, Grassmann, Frobenius et von Neumann sont parmi les célèbres mathématiciens qui ont travaillé sur la théorie de la matrice.

Olga Taussky-Todd (1906-1995) a fait des contributions importantes à la matrice théorie, l'utiliser pour enquêter sur un phénomène aérodynamique appelé ou flottant aéroélasticité cours de la Seconde Guerre mondiale . Elle a été appelé «porteur de flambeau" pour la théorie de la matrice.

Éducation

Matrices étaient traditionnellement enseignées dans le cadre de l'algèbre linéaire dans un collège ou avec le calcul. Avec l'adoption de intégré textes de mathématiques pour une utilisation à l'école secondaire dans les années 1990, ils ont été inclus par de nombreux textes tels comme le Base + Mathematics Project qui sont souvent la cible dès la neuvième année, ou plus tôt pour les honneurs étudiants. Elles nécessitent souvent l'utilisation de calculatrices graphiques comme le TI-83 qui peut effectuer des opérations complexes telles que l'inversion de matrice très rapidement.

Bien que la plupart des langages informatiques ne sont pas conçus avec des commandes ou des bibliothèques pour les matrices, dès les années 1970, certains ordinateurs de bureau d'ingénierie tels que la HP 9830 avait cartouches ROM pour ajouter des commandes de base pour matrices. Certains langages informatiques tels que APL, ont été conçus pour manipuler des matrices, et des programmes tels que mathématiques Mathematica, avec Maple, Matlab, et Octave sont également utilisés pour faciliter le calcul des matrices.

Applications

Chiffrement

Les matrices peuvent être utilisées pour crypter des données numériques. Le chiffrement est réalisé par multiplication de la matrice de données avec une matrice de touches. Le décryptage se fait simplement en multipliant la matrice chiffrée avec l'inverse de la clé.

Infographie

4 × 4 matrices de transformation sont couramment utilisés dans l'informatique graphique. La gauche 3 × 3 partie supérieure d'une matrice de transformation est composée de la nouvelle X, Y, et Z de la post-transformation de coordonnées de l'espace.

Récupéré à partir de " http://en.wikipedia.org/w/index.php?title=Matrix_(mathematics)&oldid=199124713 "