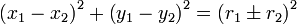Tangente
Contexte des écoles Wikipédia
Cette sélection se fait pour les écoles par la charité pour enfants en savoir plus . Parrainer un enfant de faire une réelle différence.

Dans la géométrie , la ligne de tangente (ou simplement la tangente) à une courbe à une donnée point est la ligne droite qui "touche juste" la courbe à ce point (au sens expliqué plus précisément ci-dessous). Comme il passe par le point de tangence, la tangente est "va dans le même sens" que la courbe, et en ce sens ce est la meilleure approximation linéaire à la courbe à ce point. La même définition se applique aux courbes de l'espace et des courbes dans de dimension n espace euclidien .
De la même manière, le plan tangent à une surface à un moment donné est le plan que «touche juste" la surface à ce point. Le concept d'une tangente est l'une des notions les plus fondamentales de la géométrie différentielle et a été largement généralisée - voir Espace tangent.
Le mot «tangente» vient du tangere latin, qui signifie "toucher".
Tangente à une courbe
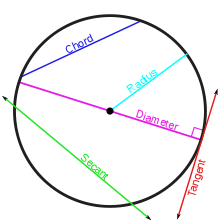
La notion intuitive qu'une tangente "touche juste" une courbe peut être rendu plus explicite en considérant la séquence de lignes droites ( lignes sécantes) passant par deux points A et B, qui se trouvent sur la courbe. La tangente en A est la limite de la progression des droites sécantes que B se déplace sans cesse plus étroite à A. L'existence et l'unicité de la tangente dépend d'un certain type de lissage mathématique, connu sous le nom "différentiabilité". Par exemple, si deux arcs de cercle se rencontrent à un point pointu (un sommet) il n'y a pas tangente définie de manière unique au sommet parce que la limite de la progression des droites sécantes dépend de la direction dans laquelle "point B" se approche du sommet.
Dans la plupart des cas fréquemment rencontrés, la tangente à une courbe ne traverse pas la courbe au point de tangence (même si elle peut, lorsqu'il a continué, traverser la courbe à d'autres endroits loin du point de tangence). Ce est le cas, par exemple, de toutes les tangentes à un cercle ou un parabole. Cependant, à des points exceptionnels appelé points d'inflexion, la tangente ne traverse la courbe au point de tangence. Un exemple est le point (0,0) sur le graphique de la parabole cubique y = x 3.
Inversement, il peut arriver que la courbe se trouve entièrement sur un côté d'une ligne droite passant par un point sur elle, et pourtant cette ligne droite ne est pas une tangente. Ce est le cas, par exemple, par une ligne passant par le sommet d'un triangle et le triangle ne interecting - où ne existe pas la ligne tangente pour les raisons expliquées ci-dessus. En géométrie convexe, ces lignes sont appelés soutenir lignes.
Approche analytique
L'idée géométrique de la tangente que la limite de droites sécantes sert de motivation pour les méthodes analytiques qui sont utilisés pour trouver des tangentes explicitement. La question de trouver la tangente à un graphique, ou le problème de la tangente, était l'une des questions centrales menant à l'élaboration de calcul dans le 17ème siècle. Dans le deuxième livre de sa géométrie René Descartes dit du problème de la construction de la tangente à une courbe, "et je ose dire que ce ne est pas seulement le problème le plus utile et le plus général en géométrie que je sais, mais même que je ai jamais désiré connaître."
Description intuitive
Supposons qu'une courbe est donnée à la représentation graphique d'une fonction y = f (x). Pour trouver la tangente au point p = (a, f (a)), envisager un autre point q proximité = (a + h, f (a + h)) sur la courbe. Le pente de la sécante passant par p et q est égal à la différence quotient
Comme le point Q se rapproche de p, ce qui correspond à faire de plus en plus petit h, le quotient de différence devrait se approcher d'une certaine valeur de limitation k, qui est la pente de la tangente au point p. Si k est connu, l'équation de la tangente peut être trouvé sous la forme de point la pente:
Description plus rigoureuse
Pour faire le raisonnement précédent rigoureuse, il faut expliquer ce qu'on entend par le quotient de différence approcher une certaine valeur limite k. La formulation mathématique précise a été donnée par Cauchy dans le 19ème siècle et est basé sur la notion de limite . Supposons que le graphe ne est pas une pause ou un bord tranchant à la p et il ne est ni plomb, ni trop près ondulée p. Ensuite, il existe une valeur unique de telle sorte que lorsque k h tend vers 0, le quotient de différence se rapproche et plus proche de k, et la distance entre eux devient négligeable par rapport à la taille de h, si h est assez petit. Cela conduit à la définition de la pente de la tangente à la courbe comme la limite des quotients de différence pour la fonction f. Cette limite est le dérivé de la fonction f au point x = a, notée f '(a). Utilisation de dérivés, l'équation de la tangente peut se énoncer comme suit:
Calcul prévoit des règles pour le calcul des dérivées des fonctions qui sont donnés par les formules, telles que la fonction de puissance, fonctions trigonométriques , fonction exponentielle , logarithme , et leurs diverses combinaisons. Ainsi équations des tangentes à des graphiques de toutes ces fonctions, ainsi que beaucoup d'autres, peuvent être trouvés par les méthodes de calcul.
Lorsque la méthode échoue
Calcul démontre également qu'il existe des fonctions et des points sur leurs graphiques pour lesquels il ne existe pas la limite déterminant la pente de la tangente. Pour ces points, la fonction f est non différentiable. Il ya deux raisons possibles pour la méthode de trouver les tangentes basées sur les limites et les dérivés à l'échec: soit la tangente géométrique existe, mais ce est une ligne verticale, qui ne peut être donnée sous la forme de point pente car il n'a pas de pente, ou le graphique est trop mal comportés à admettre une tangente géométrique.
Le graphique y = x 3.1 illustre la première possibilité: ici le quotient de différence à a = 0 est égale à 1/3 h = h / h - 2/3, ce qui devient très grand que h tend vers 0. La tangente à cette courbe à l'origine est vertical.
Le graphique y = | x | de la valeur absolue fonction se compose de deux lignes droites de pentes différentes rejoint à l'origine. Comme un point q approche l'origine de la droite, la ligne sécante a toujours pente 1. Comme un point q approche l'origine de la gauche, la ligne sécante a toujours pente -1. Par conséquent, il ne est pas tangente unique pour le graphique à l'origine (bien que dans un certain sens, il ya deux demi-tangentes, correspondant à deux directions possibles d'aborder l'origine).

Cercles tangents
Deux cercles , avec rayons de r i et centres au (x i, y i), pour i = 1, 2 sont dits être tangente à l'autre si
Surfaces et les collecteurs de dimensions supérieures
Le plan tangent à une surface en un point P donné est défini de façon analogue à la ligne tangente, dans le cas de courbes. Ce est la meilleure approximation de la surface par un plan à p, et peut être obtenue que la position de limitation des plans passant par trois points distincts sur la surface à proximité de ces points comme p convergent à p. Plus généralement, il ya un k de dimension espace tangent en chaque point d'un k de dimension collecteur de dimension n dans le espace euclidien .