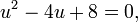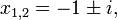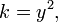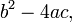Équation quadratique

Renseignements généraux

SOS Enfants a essayé de rendre le contenu plus accessible Wikipedia par cette sélection des écoles. Tous les enfants disponibles pour le parrainage de SOS Enfants des enfants sont pris en charge dans une maison de famille près de la charité. Lire la suite ...

En mathématiques , une équation quadratique est un polynôme équation de la seconde degré. La forme générale est

$ax ^ 2 + bx + c = 0, \, \!$

où a ≠ 0. (Pour a = 0, l'équation devient une équation linéaire ).

Les lettres a, b et c sont appelés : coefficients du coefficient quadratique a est le coefficient de 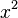$x ^ 2$ , Le coefficient linéaire b est le coefficient de x, et c est la coefficient constant, aussi appelé le terme libre ou terme constant.

Équations du second degré sont appelés quadratique parce carré est latine pour "carré"; dans le premier terme est la variable carré.

Parcelles de réelle -Évaluées quadratique fonction ax ² + bx + c, variant chaque coefficient séparément

Formule quadratique

Une équation quadratique réels ou complexes coefficients a deux solutions (pas nécessairement distinctes), appelés racines, qui peut être réel ou complexe, étant donné par la formule quadratique:

$x = \ frac {-b \ h \ sqrt {b ^ 2-4ac}} {} 2a,$

où le symbole "±" indique que les deux

$x_ + = \ frac {-b + \ sqrt {b ^ 2-4ac}} {} 2a$

$\ X_- = \ frac {-b - \ sqrt {b ^ 2-4ac}} {} 2a$

sont des solutions.

Autrement dit, ± de la plus ou moins 'des moyens que les possibilités de l'équation.

Discriminant

Exemple de signes discriminants
■ <0: x ² + _^1/2
■ = 0: - _^4/3 x ² + _^4/3 x - _^1/3
■> 0: _^3/2 x ² + _^1/2 x - _^4/3

Dans la formule ci-dessus, l'expression sous le signe de racine carrée:

$\ Delta = b ^ 2 - 4ac, \, \!$

est appelé le discriminant de l'équation quadratique.

Une équation quadratique à coefficients réels peut avoir un ou deux racines réelles distinctes, ou deux racines complexes distinctes. Dans ce cas, le discriminant détermine le nombre et la nature des racines. Il ya trois cas:

Si le discriminant est positif, il existe deux racines distinctes, qui sont tous deux des nombres réels. Pour équations du second degré avec entiers coefficients, si le discriminant est un carré parfait, les racines sont des nombres rationnels , en d'autres cas, ils peuvent être irrationnels quadratiques.
Si le discriminant est nul, il ya exactement une racine distincte, et que la racine est un nombre réel . Parfois appelé double racine, sa valeur est:
$x = - \ frac {b} {} 2a. \, \!$
Si le discriminant est négatif, il n'y a pas de véritables racines. Plutôt, il ya deux (non réel) distinctes complexes racines, qui sont complexes conjugués de l'autre:
$\ Begin {align} x & = \ frac {} {-b 2a} + i \ frac {\ sqrt {4ac - b ^ 2}}} {2a, \\ x & = \ frac {} {-b 2a} - i \ frac {\ sqrt {4ac - b ^ 2}}} {2a, \\ i ^ 2 = -1 &. \ End {align}$

Ainsi, les racines sont distinctes si et seulement si le discriminant est non nul, et les racines sont réelles si et seulement si le discriminant est non négative.

Géométrie

Pour le fonction quadratique:
f (x) = x ² - x - = 2 (x + 1) (x - 2) d'un réel variable x, x - les coordonnées des points où la courbe coupe l'axe des x, x = 1 et x = 2, sont le racines de l'équation quadratique: x ² - x - 2 = 0.

Les racines de l'équation quadratique

$ax ^ 2 + bx + c = 0, \,$

sont également la zéros de la fonction quadratique:

$f (x) = ax ^ 2 + bx + c, \,$

étant donné qu'ils sont les valeurs de x pour laquelle

$f (x) = 0 \,$

Si a, b, et c sont des nombres réels , et le domaine de f est l'ensemble des nombres réels, les zéros de f sont exactement les x - coordonnées des points où le graphe touche le axe x.

Il résulte de ce qui précède que, si le discriminant est positif, le graphique touche le axe x en deux points, si zéro, la touche graphique à un moment donné, et si elle est négative, le graphique ne touche pas l'axe des x.

Factorisation quadratique

Le terme

$x - r \,$

est un facteur du polynôme

$ax ^ 2 + bx + c, \$

si et seulement si r est un racine de l'équation quadratique

$ax ^ 2 + bx + c = 0. \$

Il résulte de la formule quadratique

$ax ^ 2 + bx + c = a \ left (x - \ frac {-b + \ sqrt {b ^ 2-4ac}} {} 2a \ right) \ left (x - \ frac {-b - \ sqrt { b ^ 2-4ac}} {2a} \ droite).$

Dans le cas particulier où le quadratique a une seule racine distincte (ce est à dire le discriminant est nul), le polynôme quadratique peut être factorisé comme

$ax ^ 2 + bx + c = a \ left (x + \ frac {b} {} 2a \ right) ^ 2. \, \!$

Application aux équations de degré supérieur

Certaines équations de degré supérieur peuvent être mis en forme quadratique et résolus de cette façon. Par exemple, l'équation 6-degré en x:

$x ^ 6 - 4x ^ 3 + 8 = 0 \,$

peut être réécrite comme:

$(X ^ 3) ^ 2-4 (x ^ 3) + 8 = 0 \ ,,$

ou, de façon équivalente, comme une équation quadratique dans une nouvelle variable u:

$u ^ 2 - 4u + 8 = 0, \,$

où

$u = x ^ 3. \,$

Résoudre l'équation quadratique pour les résultats de U dans les deux solutions:

$u = 2 \ h 2i.$

Ainsi

$x ^ 3 = 2 \ h 2i \ ,.$

Concentrant sur la recherche les trois racines de cube

- Les trois autres solutions pour x sera leur conjugués complexes - réécriture de la droite à l'aide La formule d'Euler:

$x ^ 3 = 2 ^ {\ frac {3} {2}} e ^ {\ frac {1} {4} \ pi} i = 2 ^ {\ frac {3} {2}} e ^ {\ frac { 8k + 1} {4} \ pi i} \,$

(Depuis e ^{2 k π i} = 1), donne les trois solutions:

$x = 2 ^ {\ frac {1} {2}} e ^ {\ frac {1} 8k + {12} \ pi i} \ ,, ~ k = 0, 1, 2 \ ,.$

En utilisant à nouveau la formule de Euler avec des identités trigonométriques telles que cos (π / 12) =

, Et en ajoutant les conjugués complexes, donne la collection complète de solutions que:

$x_ {1,2} = -1 \ h i, \,$

$x_ {3,4} = \ frac {1 + \ sqrt {3}} {2} \ h \ frac {1 - \ sqrt {3}} {2} i \,$

$x_ {5,6} = \ frac. {1 - \ sqrt {3}} {2} \ h \ frac {1 + \ sqrt {3}} {2} i \,$

Histoire

Les Babyloniens, le plus tôt 1800 BC (affiché sur Old babylonienne tablettes d'argile) pourraient résoudre une paire d'équations simultanées de la forme:

$x + y = p, \ \ xy = q \$

qui sont équivalentes à l'équation:

$\ X ^ 2 + q = px$

La paire originale des équations ont été résolu comme suit:

Forme $\ Frac {x + y} {2}$
Forme $\ Left (\ frac {x + y} {2} \ right) ^ 2$
Forme $\ Left (\ frac {x + y} {2} \ right) ^ 2 - xy$
Forme $\ Sqrt {\ left (\ frac {x + y} {2} \ right) ^ 2 - xy} = \ frac {xy} {2}$
Trouver $x, \ y$ par examen des valeurs dans (1) et (4).

Dans le Sulba soutras dans ancienne vers l'Inde 8e siècle avant notre ère équations du second degré de la forme ax ² = c et ax + bx ² = c ont été explorés en utilisant des méthodes géométriques. Mathématiciens babyloniens de circa 400 BCE et Mathématiciens chinois de circa 200 BCE a utilisé la méthode de complétant le carré de résoudre des équations du second degré avec racines positives, mais ne avait pas de formule générale. Euclide , le mathématicien grec, produit une méthode géométrique plus abstrait autour 300 BCE.

En 628 CE, Brahmagupta a donné la première solution explicite (bien que pas encore tout à fait général) de l'équation quadratique:

$\ Ax ^ 2 + bx = c$

Pour le nombre absolu multiplié par quatre fois la [coefficient de la] carré, ajouter le carré de la [coefficient de la] à moyen terme; la racine carrée de la même, moins le [coefficient de la] moyen terme, étant divisé par deux fois le [coefficient de la] place est la valeur. (Brahmasphutasiddhanta (traduction Colebrook, 1817, à la page 346)

Ceci est équivalent à:

$x = \ frac {\ sqrt {4ac + b ^ 2} -b} {} 2a.$

Le Bakhshali manuscrit daté avoir été écrit en Inde dans le 7ème siècle CE contenait une formule algébrique pour résoudre des équations du second degré, ainsi que quadratique équations indéterminées (à l'origine du type de hache / c = y). Mohammad bin Musa Al-kwarismi ( Perse , 9ème siècle ) ont développé un ensemble de formules qui ont travaillé pour des solutions positives. Son travail a été basé sur Brahmagupta. Abraham bar Hiyya Ha-Nasi (également connu sous le Latine nom Savasorda) introduit la solution complète pour l'Europe dans son livre Liber embadorum dans le 12ème siècle . Bhāskara II ( 1114- 1185), une indienne mathématicien - astronome, a donné la première solution générale de l'équation quadratique avec deux racines.

L'écriture du mathématicien chinois Yang Hui ( 1238- 1298 AD) représente la première dans laquelle équations du second degré à coefficients négatifs de «x» apparaissent, bien qu'il attribue cela au plus tôt Liu Yi.

Dérivation

La formule quadratique peut être obtenue par le procédé de complétant le carré, afin de rendre l'utilisation de l'identité algébrique:

$x ^ 2 + 2xy + y ^ 2 = (x + y) 2 ^. \, \!$

Divisant l'équation quadratique

$ax ^ 2 + bx + c = 0 \, \!$

par un (qui est permis, car un est non nul), donne:

$x ^ 2 + \ frac {b} {a} x + \ frac {c} {a} = 0, \, \!$

$x ^ 2 + \ frac {b} {a} x = - \ frac {c} {a} \ qquad (1)$

L'équation quadratique est maintenant dans une forme dans laquelle la méthode de l'achèvement du carré peut être appliquée. Pour "compléter le carré" est de trouver une certaine constante k telle que

$x ^ 2 + \ frac {b} {a} x + k = x ^ 2 + 2xy + y ^ 2, \, \!$

pour un autre y constante. Pour que ces équations pour être vrai,

$\ Frac {b} {a} = 2y \!$

$y = \ frac {b} {2a} \, \!$

$k = y ^ 2, \, \!$

ainsi

$k = \ frac {b ^ 2} {4a ^ 2}. \, \!$

Ajout de cette constante de l'équation (1) produit

$x ^ 2 + \ frac {b} {a} x + \ frac {b ^ 2} {4a ^ 2} = - \ frac {c} {a} + \ frac {b ^ 2} {4a ^ 2} \. , \!$

Le côté gauche est maintenant carré parfait parce

$x ^ 2 + \ frac {b} {a} x + \ frac {b ^ 2} {4a ^ 2} = \ left (x + \ frac {b} {} 2a \ right) ^ 2$

Le côté droit peut être écrit comme une seule fraction, avec un dénominateur commun 4 ^2. Cela donne

$\ Left (x + \ frac {b} {} 2a \ right) ^ 2 = \ frac {b ^ 2-4ac} {4a ^ 2}.$

Prenant la racine carrée des deux côtés rendements

$\ Left | x + \ frac {b} {} 2a \ right | = \ frac {\ sqrt {b ^ 2-4ac \}} {| 2a |} \ Rightarrow x + \ frac {b} {} 2a = \ h \ frac {\ sqrt {b ^ 2-4ac \ {}}} 2a.$

Isolement de x, donne

$x = - \ frac {b} {2a} \ h \ frac {\ sqrt {b ^ 2-4ac \ {}}} = 2a \ frac {-b \ h \ sqrt {b ^ 2-4ac \}} { 2a}.$

Formule de rechange

Dans certaines situations, il est préférable d'exprimer les racines dans une forme alternative.

$x = \ frac {} {2c - b \ mp \ sqrt {b ^ 2-4ac \}}.$

Cette alternative nécessite c être différent de zéro; pour, si c est égal à zéro, la formule donne correctement zéro comme une racine, mais ne donne aucune seconde racine, non nul. Au lieu de cela, l'un des deux choix pour un produit ∓ division par zéro, ce qui ne est pas définie.

Les racines sont les mêmes quel que soit l'expression que nous utilisons; l'autre forme est simplement une variation algébrique de la forme commune:

$\ Begin {align} \ frac {-b + \ sqrt {b ^ 2-4ac \}} {} & 2a {} = \ frac {-b + \ sqrt {b ^ 2-4ac \}} {2a} \ cdot \ frac {-b - \ sqrt {b ^ 2-4ac \}} {- b - \ sqrt {b ^ 2-4ac \}} \\ & {} = \ frac {} {4ac 2a \ gauche (- b - \ sqrt {b ^ 2-4ac} \ right)} \\ & {} = \ frac {} {2c - b - \ sqrt {b ^ 2-4ac \}}. \ End {align}$

La formule de remplacement peut réduire la perte de précision dans l'évaluation numérique des racines, qui peut être un problème si l'une des racines est beaucoup plus petit que l'autre en valeur absolue. Le problème de c pouvant être zéro peut être évité en utilisant une approche mixte:

$x_1 = \ frac {-b - \ sgn b \, \ sqrt {b ^ 2-4ac}} {} 2a,$

$x_2 = \ frac {c} {} ax_1.$

Ici sgn désigne la fonction signer.

Mise en œuvre en virgule flottante

Une attention point de la mise en œuvre informatique flottante diffère un peu des deux formes pour produire un résultat robuste. En supposant que le discriminant, b ² -4 ac, est positif et b est non nul, le code sera quelque chose comme ce qui suit.

$t: = - \ tfrac12 \ big (b + \ SGN (b) \ sqrt {b ^ 2-4ac} \ big) \, \!$

$r_ {1}: = t / a \, \!$

$r_ {2}: = c / t \, \!$

Voici SGN (b) est le fonction signe, où sgn (b) est une si b est positif et -1 si b est négatif; son utilisation assure que les quantités ajoutées sont de même signe, en évitant annulation catastrophique. Le calcul de R ₂ utilise le fait que le produit des racines est c / a.

Les formules de Viète

Les formules de Viète donnent une relation simple entre les racines d'un polynôme et de ses coefficients. Dans le cas du polynôme quadratique, ils prennent la forme suivante:

$x_ + + x_- = - \ frac {b} {a}$

$x_ + \ cdot x_- = \ frac {c} {a}.$

La première formule ci-dessus donne une expression commode pour la représentation graphique d'une fonction quadratique. Comme le graphe est symétrique par rapport à une ligne verticale passant par le sommet, quand il ya deux racines réelles du vertex les coordonnées X est situé à la moyenne des racines (ou interceptions). Ainsi, les coordonnées x du sommet est donnée par l'expression:

$x_V = \ frac {x_ + + x_-} {2} = - \ frac {b} {} 2a.$

La coordonnée y peut être obtenue en substituant le résultat ci-dessus dans l'équation quadratique donné, ce qui donne

$y_V = - \ frac {b ^ 2} {} 4a + c = - \ frac {b ^ 2 - 4ac} {} 4a.$

Généralisations

La formule et sa dérivation restent correctes si les coefficients a, b et c sont des nombres complexes , ou plus généralement des membres de l'une champ dont caractéristique ne est pas 2. (Dans un corps de caractéristique 2, l'élément 2 est un zéro et il est impossible de diviser par elle.)

Le symbole

$\ H \ sqrt {b ^ 2-4ac}$

dans la formule doit être comprise comme «l'un des deux éléments dont le carré est

$b ^ 2-4ac, \,$

si ces éléments existent. Dans certains domaines, certains éléments ne ont pas de racines carrées et certains ont deux; zéro seulement a juste une racine carrée, sauf dans les corps de caractéristique 2. Notez que même si un champ ne contient pas une racine carrée de un nombre, il ya toujours un quadratique champ d'extension qui fait, de sorte que la formule quadratique fera toujours sens comme une formule dans ce domaine d'extension.

Caractéristique 2

Dans un corps de caractéristique 2, la formule quadratique, qui se appuie sur deux étant un unité, ne tient pas. Considérons le polynôme quadratique unitaire

$\ Displaystyle x ^ {2} + bx + c$

sur un corps de caractéristique 2. Si b = 0, alors la solution réduit à extraire une racine carrée, de sorte que la solution est

$\ Displaystyle x = \ sqrt {c}$

et notez qu'il n'y a qu'une seule racine depuis

$\ Displaystyle - \ sqrt {c} = - \ sqrt {c} + 2 \ sqrt {c} = \ sqrt {c}.$

En résumé,

$\ Displaystyle x ^ {2} + c = (x + \ sqrt {c}) ^ {2}.$

Voir résidu quadratique pour plus d'informations sur l'extraction des racines carrées dans des domaines finis.

Dans le cas où b ≠ 0, il existe deux racines distinctes, mais si le polynôme est irréductible, ils ne peuvent être exprimés en termes de racines carrées des chiffres dans le champ de coefficient. Au contraire, définir la racine R-2 (c) de c à une racine du polynôme x ² + x + c, un élément de la domaine de fractionnement de ce polynôme. On vérifie que R (c) + 1 est également une racine. En termes de l'opération 2-root, les deux racines de la (non-unitaire) hache quadratique ² + bx + c sont

$\ Frac {b} {a} R \ gauche (\ frac {} {b ac ^ 2} \ right)$

$\ Frac {b} {a} \ left (R \ gauche (\ frac {} {b ac ^ 2} \ right) 1 \ right).$

Par exemple, Soit A un générateur multiplicatif du groupe d'unités de F _4, le Corps de Galois d'ordre quatre (d'où a et a + 1 sont les racines de x ² + x + 1 sur ₄ F). Parce que (a + 1) ² = a, a + 1 est la solution unique de l'équation quadratique x ² + a = 0. D'autre part, le polynôme x + ax + 1 est irréductible sur F _4, F, mais se sépare plus de _16, où il a les deux racines ab et ab + a, où b est une racine de x ² + x + a dans F _16.

Ce est un cas particulier de La théorie d'Artin-Schreier.

Livre

Vedic Mathematics: Seize simple mathématique formules des Védas, par Swami Sankaracarya (1884-1960), Motilal Banarsidass Indological éditeurs et des libraires, Varnasi, Inde, 1965; réimprimé à Delhi, en Inde, 1975, 1978. 367 pages.

Récupéré à partir de " http://en.wikipedia.org/w/index.php?title=Quadratic_equation&oldid=199164119 "