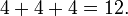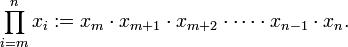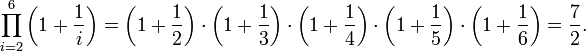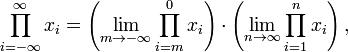Multiplication

À propos de ce écoles sélection Wikipedia

SOS Enfants a fait cette sélection Wikipedia aux côtés d'autres écoles des ressources . Un lien rapide pour le parrainage d'enfants est http://www.sponsor-a-child.org.uk/

3 x 4 = 12, de sorte que douze points peuvent être disposés en trois rangées de quatre (ou quatre colonnes de trois).

Multiplication des nombres entiers est le opération mathématique de l'addition des copies multiples du même numéro. Par exemple, quatre multiplié par trois, ce est douze, étant donné que trois ensembles de quatre font douze:

$4 + 4 + 4 = 12. \! \,$

La multiplication peut également être considéré comme un objet de comptage disposés dans un rectangle ou trouver la zone de rectangle dont les côtés ont donné longueurs.

La multiplication est l'une des quatre opérations principales en arithmétique élémentaire , et la plupart des gens apprennent multiplication de base des algorithmes de école primaire. L'inverse de la multiplication est la division .

Multiplication est généralisée à toutes sortes de chiffres et à des constructions plus abstraites comme des matrices.

Notation et la terminologie

La multiplication est écrite en utilisant le signe de multiplication "×" entre les termes; ce est-à notation infixée. Le résultat est exprimé avec une signe égal. Par exemple,

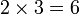$2 \ times 3 = 6$ (Verbalement, "deux fois trois égalent six")

$3 \ 4 fois = 12$

$2 \ 3 \ fois fois 5 = 30$

$2 \ \ fois 2 fois 2 \ fois 2 \ times 2 = 32$

Il ya plusieurs autres notations communes pour la multiplication:

La multiplication est parfois désigné par un navigateur point du milieu ou d'un période:
$5 \ cdot 2 \ quad \ text {ou} \ quad 5 \,. \, 2$
Le point central est la norme dans le États-Unis , le Royaume-Uni et d'autres pays où la durée est utilisé comme virgule. Dans certains pays qui utilisent une virgule comme séparateur décimal, la période est utilisée pour la multiplication place.
Le astérisque (* 2 5 par exemple) est souvent utilisé avec des ordinateurs, car il apparaît sur chaque flèche. Cet usage origine dans le Langage de programmation FORTRAN.
En algèbre , la multiplication impliquant des variables est souvent écrit comme un juxtaposition (par exemple pour xy x y fois ou 5 x à cinq fois x). Cette notation peut également être utilisée pour les nombres qui sont entourés par parenthèses (par exemple 5 (2) ou (5) (2) pour deux à cinq reprises).

Les chiffres à multiplier sont généralement appelés les «facteurs» ou «multiplicandes". Quand on pense que la multiplication addition répétée, le nombre d'être répété est appelé le "multiplicande", tandis que le nombre de répétitions est appelé le «multiplicateur». En algèbre, un nombre qui est multiplié par une variable ou une expression (ce est à dire 3 en 3 xy ²⁾ est appelé coefficient.

Le résultat de la multiplication est appelée produit, et est un multiples de chaque facteur. Par exemple 15 est le produit de trois et cinq, et est à la fois un multiple de 3 et un multiple de cinq.

Calcul

Les méthodes standard pour la multiplication de nombres en utilisant crayon et du papier nécessitent une table de multiplication de produits mémorisés ou consultés de petits nombres (généralement deux numéros 0-9), mais une méthode, le algorithme de multiplication paysanne, ne fonctionne pas. Beaucoup de programmes de mathématiques développé selon les normes de la 1989 NCTM ne enseignent pas de méthodes arithmétiques standard, au lieu guider les étudiants à inventer leurs propres méthodes de calcul. Bien que largement adopté par de nombreux districts scolaires dans des pays comme les Etats-Unis, ils se sont heurtés à la résistance de certains parents et mathématiciens, et certains districts ont abandonné depuis ces programmes en faveur des mathématiques traditionnelles.

En multipliant le nombre à plus de deux décimales à la main est fastidieux et source d'erreurs. Logarithmes communs ont été inventées pour simplifier ces calculs. Le règle à calcul a permis chiffres pour être rapidement multipliés à environ trois lieux de précision. Dès le début du XXe siècle , mécaniques calculatrices , comme le Marchant, la multiplication automatique de jusqu'à 10 chiffres. Électroniques modernes ordinateurs et calculatrices ont considérablement réduit la nécessité pour la multiplication à la main.

Algorithmes historiques

Méthodes de multiplication ont été documentés dans le égyptienne , la Grèce , Babylone , vallée de l'Indus , et chinois civilisations.

Egyptiens

La méthode égyptienne de la multiplication de nombres entiers et fractions, documenté dans le Ahmès Papyrus, était par ajouts successifs et doublement. Par exemple, pour trouver le produit des 13 et 21 il fallait doubler 21 trois fois, obtenir une × 21 = 21, 2 × 21 = 42, 4 × 21 = 84, 8 × 21 = 168. Le produit complet pourrait alors trouvé en ajoutant les termes appropriés trouvés dans la séquence de doublement:

13 × 21 = (1 + 4 + 8) x 21 = (1 x 21) + (4 x 21) + (8 x 21) = 21 + 84 + 168 = 273.

Babyloniens

Les Babyloniens ont utilisé un sexagésimal système de numération positionnel, analogue à l'époque moderne système décimal. Ainsi, la multiplication babylonienne était très semblable à virgule moderne multiplication. En raison de la relative difficulté de se souvenir de 60 × 60 produits différents, mathématiciens babyloniens employés tables de multiplication. Ces tableaux ont consisté d'une liste des vingt premiers multiples d'un certain nombre principale n: n, 2 n, ..., 20 n; suivie des multiples de 10 n: 30 n 40 n, et 50 n. Ensuite, pour calculer un produit sexagésimal, dire 53 n, une seule suffit d'ajouter 50 n et 3 n calculée à partir de la table.

Chinois

Dans les livres, Chou Pei Suan Ching daté avant 300 avant JC, et de la Neuf chapitres sur l'art mathématique, les calculs de multiplication ont été écrits en mots, bien que les premiers mathématiciens chinois employés un boulier dans les calculs de la main d'addition et de multiplication.

Vallée de l'Indus

Produit de 45 et 256. Remarque l'ordre des chiffres de 45 est inversé en bas de la colonne de gauche. L'étape de report de la multiplication peut être effectuée à la dernière étape du calcul (en gras), retournant le produit final de 45 x 256 = 11 520.

Les mathématiciens hindous début de la région de la vallée de l'Indus ont utilisé une variété de trucs intuitives pour effectuer la multiplication. La plupart des calculs ont été effectués sur de petits comprimés d'ardoise à la main, en utilisant des tables de craie. Une technique a été que de multiplication treillis (ou gelosia multiplication). Voici un tableau a été élaboré avec les lignes et les colonnes marquées par les multiplicandes. Chaque boîte de la table a été divisée en deux en diagonale, comme triangulaire treillis. Les entrées de la table lieu les produits partiels, écrites sous forme de nombres décimaux. Le produit peut ensuite être formé en additionnant vers le bas des diagonales du treillis.

Méthode moderne

La méthode moderne de multiplication sur la base du Système de numération indo-arabe a été décrite par Brahmagupta. Brahmagupta a donné des règles pour l'addition, la soustraction, la multiplication et la division. Henry Burchard fine, puis professeur de mathématiques à l'Université de Princeton , a écrit ce qui suit:

Les Indiens sont les inventeurs non seulement du système décimal de position elle-même, mais de la plupart des processus impliqués dans la prise en compte élémentaire avec le système. Addition et soustraction ils ont joué tout à fait aussi qu'ils sont effectués de nos jours; multiplication qu'ils effectuent à bien des égards, le nôtre parmi eux, mais ils l'ont fait cumbrously division.

Produits des séquences

notation pi Capital

Le produit d'une séquence de termes peut être écrit avec le symbole de produits, qui découle de la capitale lettre Π (Pi) dans le alphabet grec . position de Unicode U + 220F (Π) est définie -aire un produit de n à cette fin, distinct de U + 03A0 (Π), la lettre. Ceci est défini comme:

$\ Prod_ {i = m} ^ {n} x_ {i}: = x_ {m} \ cdot x_ {m + 1} \ cdot x_ {m + 2} \ cdot \ cdots \ cdot x_ {n-1} \ cdot x_ {n}.$

L'indice donne le symbole d'une variable muette ( $Je$ dans notre cas) et sa valeur inférieure ( $m$ ); l'exposant donne sa valeur supérieure. Ainsi, par exemple:

$\ Prod_ {i = 2} ^ {6} \ left (1 + {1 \ over i} \ right) = \ left (1 + {1 \ over 2} \ right) \ cdot \ left (1 + {1 \ plus de 3} \ right) \ cdot \ left (1 + {1 \ over 4} \ right) \ cdot \ left (1 + {1 \ over 5} \ right) \ cdot \ left (1 + {1 \ over 6 } \ right) = {7 \ over 2}.$

Dans le cas où m = n, la valeur du produit est la même que celle du facteur x _m. Si m> n, le produit est le vide produit, avec la valeur 1.

Produits infinis

On peut aussi considérer les produits de infinité de termes; ceux-ci sont appelés produits infinis. Notationally, nous remplacerions n ci-dessus par le lemniscate (symbole de l'infini) ∞. Dans les réels, le produit d'une telle série est défini comme la limite du produit de la première $n$ termes, que $n$ croît sans borne. Ce est, par définition,

$\ Prod_ {i = m} ^ {\ infty} x_ {i} = \ lim_ {n \ to \ infty} \ prod_ {i = m} ^ {n} x_ {i}.$

On peut de même remplacer $m$ avec l'infini négatif, et de définir:

$\ Prod_ {i = - \ infty} ^ \ infty x_i = \ left (\ lim_ {m \ To-\ infty} \ prod_ {i = m} ^ 0 x_i \ right) \ cdot \ left (\ lim_ {n \ à \ infty} \ prod_ {i = 1} ^ n x_i \ right),$

prévues deux limites existent.

Interprétation

Produit cartésien

La définition de la multiplication comme répété addition fournit un moyen de parvenir à une interprétation théorique de réglage de la multiplication de nombres cardinaux . Dans l'expression

$\ Displaystyle a \ cdot n = \ underbrace {a + \ cdots + a} _ {n},$

si les n copies d'un doivent être combinées en union disjointe il est clair qu'ils doivent être disjoints; un moyen évident de le faire est d'utiliser un ou n que l'indexation prévue pour l'autre. Ensuite, les membres de $un \ cdot n \,$ sont exactement ceux de la Produit cartésien $une fois \ n \,$ . Les propriétés de l'opération de multiplication comme se appliquant à des nombres naturels suivent alors trivialement des propriétés correspondantes du produit cartésien.

Propriétés

Pour les nombres entiers, les fractions, réelle et les nombres complexes, la multiplication possède certaines propriétés:

Commutativité: L'ordre dans lequel deux nombres sont multipliés n'a pas d'importance.; · x · y = y x.

Associativité: Problèmes impliquant uniquement la multiplication sont invariantes par rapport à ordre des opérations.; (X · y) · z = x · (y · z).

Distributivité: Dit par rapport à l'addition sur la multiplication. Cette identité est d'une importance primordiale dans la simplification des expressions algébriques.; · x (y + z) = x · y · z + x.

élément d'identité: de la multiplication est une; tout multiplié par lui-même est une. Ceci est connu comme la propriété d'identité; · x 1 = x.

Élément zéro: Tout multiplié par zéro est égal à zéro. Ceci est connu comme étant la propriété de multiplication zéro.; x 0 = 0 ·

Propriété inverse: Chaque nombre x, sauf zéro, a une inverse multiplicatif, 1 / x, de telle sorte que x · (1 / x) = 1.

la préservation de commande: Multiplication par un nombre positif préserve Pour: si un> 0, alors si b> c alors une · b> a · c. Multiplication par un nombre négatif inverse l'ordre: si un <0, alors si b> c · b alors un <a · c.

Négatif une fois ne importe quel nombre est égal à la valeur négative de ce nombre.

(-1) · X = (- x)

Une fois l'inverse négatif est positif.

(-1) · (-1) = 1

D'autres systèmes mathématiques qui comprennent une opération de multiplication peuvent ne pas avoir toutes ces propriétés. Par exemple, la multiplication ne est pas, en général, pour des matrices et commutative quaternions.

Preuves

Toutes ces propriétés ne sont pas indépendants; certains sont une conséquence des autres. Une propriété qui peut être prouvé par les autres est la propriété zéro de multiplication. Il est prouvé au moyen de la propriété distributive. Nous supposons toutes les propriétés habituelles d'addition et de soustraction, et - x signifie la même chose que

x · 0

= (X · 0) + x - x

= (X · 0) + (x · 1) - x

= X · (0 + 1) - x

= (X · 1) - x

= X - x

= 0.

Donc, nous avons prouvé:

· x 0 = 0.

L'identité (-1) · x = (- x) peut également être prouvé en utilisant la propriété distributive:

(-1) · X

= (-1) · X + x - x

= (-1) · X · x + 1 - x

= (-1 + 1) · x - x

= 0 · x - x

= 0 - x

= - X

La preuve que (-1) · (-1) = 1 est maintenant facile:

(-1) · (-1)

= - (- 1)

= 1.

Multiplication avec les axiomes de Peano

Dans le livre Arithmetices principia, nova methodo exposita, Giuseppe Peano a proposé un nouveau système pour la multiplication à partir de ses axiomes pour nombres naturels.

a × 1 = a
A × B '= (a × b) + un

Ici, b 'représente la successeur de b, ou le nombre entier naturel qui suit b. Avec son autre neuf axiomes, il est possible de prouver règles communes de la multiplication, telles que les propriétés de distribution ou associatives.

Multiplication avec la théorie des ensembles

Il est possible, bien que difficile, pour créer une définition récursive de multiplication avec la théorie des ensembles. Un tel système repose généralement sur la définition de peano de la multiplication.

Multiplication en théorie des groupes

Il est facile de montrer qu'il ya un groupe pour multiplication- non nuls nombres rationnels. Multiplication avec les nombres non nuls satisfait

Fermeture - Pour tout a et b dans le groupe, a × b est dans le groupe.
Associativité - Ce est juste la propriété associative: (a × b) × c = a × (b × c)
Identité - Cela découle directement de la définition de Peano. Tout est multiplié par lui-même.
Inverse - Tous les numéros non-zéro ont une inverse multiplicatif.

Multiplication est aussi un groupe abélien, car il suit la propriété commutative.

a × b = b × a

La multiplication des différents types de numéros

Numéros peuvent compter (3 pommes), pour (la 3e pomme), ou de la mesure (3,5 pieds de haut); que l'histoire des mathématiques a progressé de compter sur nos doigts à la mécanique de la modélisation Quantuum, la multiplication a été généralisé à des types plus complexes et abstraits de chiffres et à des choses qui ne sont pas des numéros (comme matrices ) ou ne ressemble pas beaucoup à nombre (tel que quaternions).

Les entiers N × M est la somme des M copies de N lorsque N et M sont des nombres entiers positifs. Cela donne le nombre de choses dans un tableau large et N M élevé. Généralisation à des nombres négatifs peut être effectué par (N x -M) = - (N x M).

Rationnels Généralisation aux fractions A / B × C / D est en multipliant les numérateurs et des dénominateurs respectivement: A / B × C / D = (A × B) / (C × D). Cela donne à l'aire d'un rectangle A / B élevé et C / D de large, et est le même que le nombre de choses dans un tableau lorsque les nombres rationnels se trouvent être des nombres entiers.

Reals x × y est la limite des produits des termes correspondants dans certaines séquences de rationnels qui convergent vers x et y, respectivement, et est important dans Calculus . Cela donne à l'aire d'un rectangle et y x hauteur large. Voir ci-dessus .

Complexe Considérant nombres complexes Z1 et Z2 comme couples ou des nombres réels (a1, b1) et (a2, b2), le produit de z1 z2 est × (a1 × a2 - b2 b1 ×, a1 a2 + b2 × × b1). Ce est le même que pour les nombres réels, x a1 a2, lorsque les parties imaginaires B1 et B2 sont égaux à zéro.

D'autres généralisations Voir ci-dessus et Multiplicatif groupe, qui comprend par exemple la multiplication de matrices. Un très générale et abstraite, concept de multiplication est que la (seconde) opération binaire "multiplicativement notée" dans un anneau. Un exemple d'une bague qui ne est pas l'un des systèmes de numéro ci-dessus est anneaux de polynômes (vous pouvez ajouter et multiplier des polynômes, mais polynômes sont pas des chiffres dans tous les sens d'habitude.)

Souvent Division division x / y est la même que la multiplication par l'inverse, x × (1 / y). Multiplication pour certains types de "numéros" peut avoir division correspondante, sans inverses; dans une Domaine intégrante x peut ne avoir aucun inverse "1 / x", mais x / y peut être définie. Dans un Corps il ya inverses mais ils ne sont pas commutative (depuis 1 / x X 1 / y ne est pas le même que 1 / y X 1 / x, x / y peut être ambiguë).

Récupéré à partir de " http://en.wikipedia.org/w/index.php?title=Multiplication&oldid=204703373 "