
Nombre naturel
Renseignements généraux
Cette sélection Wikipedia est déconnecté disponibles à partir enfants SOS pour la distribution dans le monde en développement. SOS Children travaille dans 45 pays africains; pouvez-vous aider un enfant en Afrique ?
En mathématiques , un nombre naturel (aussi appelé numéro de comptage) peut signifier soit un élément de l'ensemble { 1 , 2, 3, ...} (la positifs entiers ) ou un élément de l'ensemble { 0 , 1, 2, 3, ...} (la des nombres entiers non négatifs). L'ancien est généralement utilisé dans la théorie des nombres , tandis que le second est préféré dans la logique mathématique, théorie des ensembles , et informatique . Voir ci-dessous pour une définition formelle.
Nombres naturels ont deux objectifs principaux: ils peuvent être utilisés pour comptant ("il ya trois pommes sur la table"), et ils peuvent être utilisés pour commande ("ce est le 3 ème plus grande ville dans le pays").
Propriétés des nombres naturels liés à la divisibilité , tels que la répartition des nombres premiers , sont étudiés dans la théorie des nombres . Les problèmes concernant le comptage, comme Théorie Ramsey, sont étudiées en combinatoire .

Historique des nombres naturels et l'état de zéro
Les nombres naturels avaient leurs origines dans les mots utilisés pour compter les choses, en commençant par le numéro un.
La première avancée majeure dans l'abstraction était l'utilisation de chiffres pour représenter des nombres. Cela a permis à des systèmes à développer pour enregistrer un grand nombre. Par exemple, les Babyloniens ont développé un puissant système de valeur de base essentiellement sur les chiffres de 1 et 10. L'ancienne Egyptiens avaient un système de chiffres avec distincte hiéroglyphes pour 1, 10, et toutes les puissances de 10 jusqu'à un million. Une sculpture sur pierre de Karnak, datant d'environ 1500 avant JC et maintenant à la Louvre à Paris, représente 276 que deux centaines, dizaines, 7 et 6 unités; et de même pour le nombre 4622.
Une avance beaucoup plus tard dans l'abstraction était le développement de l'idée de zéro comme un nombre avec son propre numéro. Un zéro chiffres avait été utilisé dans la notation de valeur de dès 700 avant JC par les Babyloniens, mais, ils ont omis quand il aurait été le dernier symbole du nombre. Le olmèque et civilisation maya utilisé zéro comme un numéro distinct dès le 1er siècle avant JC, apparemment développé indépendamment, mais cet usage ne se propage pas au-delà Méso-Amérique. Le concept tel qu'il est utilisé dans les temps modernes avec l'origine indienne mathématicien Brahmagupta en 628. Néanmoins, médiévale computists (calculatrices de Pâques ), en commençant par Denys le Petit au 525, utilisé à zéro comme un nombre sans l'aide d'un chiffre romain pour l'écrire. Au lieu nullus, le mot latin pour «rien», a été employé. La première étude systématique des nombres comme abstractions (ce est, aussi abstraite entités) est généralement crédités aux grecs philosophes Pythagore et Archimède . Cependant, des études indépendantes ont également eu lieu à peu près au même moment dans l'Inde , la Chine , et Méso-Amérique.
Au XIXe siècle, un set-théorique définition des nombres naturels a été développée. Avec cette définition, il est plus commode d'inclure zéro (correspondant à la ensemble vide) comme un nombre naturel. Cette convention est suivie par set théoriciens , logiciens , et des informaticiens . D'autres mathématiciens, principalement les théoriciens des nombres , préfèrent souvent suivre la tradition plus ancienne et considèrent zéro ne pas être un nombre naturel.
Notation
Les mathématiciens utilisent N ou  (N dans un tableau noir gras, affiché comme ℕ en Unicode) se référer à la ensemble des nombres naturels. Cet ensemble est infini dénombrable: il est infini, mais dénombrable par définition. Ce est également exprimé en disant que le nombre cardinal de l'ensemble est Module: Aleph_number ( parler · · hist · · liens · sous-pages essais - (résultats)
(N dans un tableau noir gras, affiché comme ℕ en Unicode) se référer à la ensemble des nombres naturels. Cet ensemble est infini dénombrable: il est infini, mais dénombrable par définition. Ce est également exprimé en disant que le nombre cardinal de l'ensemble est Module: Aleph_number ( parler · · hist · · liens · sous-pages essais - (résultats)  ).
).
Pour être sans ambiguïté quant à savoir si zéro est inclus ou non, parfois un indice "0" est ajouté dans le premier cas, et un exposant "*" est ajoutée dans ce dernier cas:
- ℕ 0 = {0, 1, 2, ...}; ℕ * = {1, 2, ...}.
(Parfois, un indice ou exposant «+» est ajouté pour signifier «positive». Toutefois, cela est souvent utilisé pour "non négatif" dans les autres cas, R + = [0, ∞) et Z + = {0, 1, 2, ...}, au moins dans la littérature européenne. La notation "*", cependant, est la norme pour une valeur non nulle ou non éléments inversibles.)
Certains auteurs qui excluent zéro des naturels utilisent les nombres entiers terme, notée  , Pour l'ensemble des entiers positifs. D'autres utilisent la notation
, Pour l'ensemble des entiers positifs. D'autres utilisent la notation  pour les entiers positifs.
pour les entiers positifs.
Set théoriciens désignent souvent l'ensemble des nombres naturels par une lettre minuscule grecque omega: ω. Lorsque cette notation est utilisée, zéro est explicitement inclus comme un nombre naturel.
Propriétés algébriques
| addition | multiplication | |
| fermeture: | a + b est un nombre naturel | a × b est un nombre naturel |
| associativité : | a + (b + c) = (a + b) + c | a × (b × c) = (a × b) x c |
| commutativité : | a + b = b + a | a × b = b × a |
| existence d'un élément de l'identité: | a + 0 = a | a × 1 = a |
| distributivité: | a × (b + c) = (a × b) + (a × c) | |
| Aucun diviseurs de zéro: | si ab = 0, soit a = 0 ou b = 0 (ou les deux) | |
Les définitions officielles
Historiquement, la définition mathématique précise des nombres naturels développé avec une certaine difficulté. Le Peano postule conditions de l'Etat que toute définition retenue doit satisfaire. Certaines constructions montrent que, compte tenu de la théorie des ensembles , modèles des postulats Peano doivent exister.
Axiomes de Peano
- Il se agit d'un nombre naturel 0.
- Chaque un nombre naturel a un successeur de nombre naturel, notée S (a).
- Il n'y a pas nombre naturel dont le successeur est 0.
- Nombres naturels distincts ont successeurs distinctes: si a ≠ b, alors S (a) ≠ S (b).
- Si une propriété est possédé par 0 et aussi par le successeur de chaque nombre naturel qui possède, alors il est possédé par tous les nombres naturels. (Ce postulat se assure que la technique de preuve induction mathématique est valide.)
Il convient de noter que le "0" dans la définition ci-dessus ne correspondant pas nécessairement à ce que nous considérons normalement être le numéro zéro. "0" signifie simplement un objet que lorsqu'il est combiné avec une fonction successeur approprié, satisfait les axiomes de Peano. Tous les systèmes qui répondent à ces axiomes sont isomorphes, le nom de «0» est utilisé ici pour le premier élément, qui est le seul élément qui ne est pas un successeur. Par exemple, les nombres naturels commençant par une satisfont également aux axiomes.
Constructions basé sur la théorie des ensembles
Une construction standard
Une construction standard dans la théorie des ensembles , un cas particulier de l' ordinal von Neumann construction, est de définir les nombres naturels comme suit:
- Nous avons mis en 0: = {}, le ensemble vide,
- et définir S (A) = A ∪ {a} pour chaque ensemble a. S (a) est le successeur d'un, et S est appelée la fonction successeur.
- Si le axiome de l'infini est vérifiée, alors l'ensemble des nombres naturels existe et est l'intersection de tous les ensembles contenant 0 qui sont fermés sous cette fonction successeur.
- Si l'ensemble des nombres naturels existe, alors il satisfait la Axiomes de Peano.
- Chaque nombre naturel est alors égal à l'ensemble des nombres naturels inférieurs à elle, de sorte que
- 0 = {}
- 1 = {0} = {{}}
- 2 = {0,1} = {0, {0}} = {{}, {{}}}
- 3 = {0,1,2} = {0, {0}, {0, {0}}} = {{}, {{}}, {{}, {{}}}}
- n = {0,1,2, ..., n-2, n-1} = {0,1,2, ..., n} -2 ∪ {n} -1 = (n-1) ∪ {n} -1
- et ainsi de suite. Quand vous voyez un certain nombre naturel utilisé comme un ensemble, ce est typiquement ce que l'on entend. Selon cette définition, il ya exactement n éléments (au sens naïve) dans l'ensemble n et n ≤ m (au sens naïve) si et seulement si n est égal à un sous-ensemble de m.
- Aussi, avec cette définition, différentes interprétations possibles de notations comme R n (n-tuples contre mappages de n dans R) coïncident.
- Même si l'axiome de l'infini ne existe pas et ne l'ensemble des nombres naturels, il est possible de définir ce que cela signifie d'être un de ces ensembles. Un ensemble n est un nombre naturel signifie que ce est soit 0 (vide) ou d'un successeur, et chacun de ses éléments est soit 0, soit le successeur d'un autre de ses éléments.
D'autres constructions
Bien que la construction standard est utile, ce ne est pas la seule construction possible. Par exemple:
- on pourrait définir 0 = {}
- et S (a) = {a},
- production
- 0 = {}
- 1 = {0} = {{}}
- 2 = {1} = {{{}}}, etc.
Ou nous pourrions même définir 0 = {{}}
- et S (A) = U {a}
- production
- 0 = {{}}
- 1 = {{}, {0} = {}, {{}}}
- 2 = {{}, 0, 1}, etc.
Sans doute la plus ancienne définition d'ensemble théorie des nombres naturels est la définition communément attribué à Frege et Russell en vertu duquel chaque concrète nombre naturel n est défini comme l'ensemble de tous les ensembles à n éléments. Cela peut paraître circulaire, mais peut être fait avec soin rigoureuse. Définir 0 comme  (Clairement l'ensemble de tous les ensembles avec 0 éléments) et de définir
(Clairement l'ensemble de tous les ensembles avec 0 éléments) et de définir  (Pour tout ensemble A)
(Pour tout ensemble A)  . Puis 0 sera l'ensemble de tous les ensembles avec 0 éléments,
. Puis 0 sera l'ensemble de tous les ensembles avec 0 éléments,  sera l'ensemble de tous les ensembles avec 1 élément,
sera l'ensemble de tous les ensembles avec 1 élément, 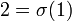 sera l'ensemble de tous les ensembles avec deux éléments, et ainsi de suite. L'ensemble des nombres naturels peut être définie comme l'intersection de tous les ensembles contenant 0 comme élément et close par
sera l'ensemble de tous les ensembles avec deux éléments, et ainsi de suite. L'ensemble des nombres naturels peut être définie comme l'intersection de tous les ensembles contenant 0 comme élément et close par  (Qui est, si l'ensemble contient un élément n, il contient également
(Qui est, si l'ensemble contient un élément n, il contient également  ). Cette définition ne fonctionne pas dans les systèmes habituels de la théorie des ensembles axiomatique parce que les collections impliquées sont trop grandes (il ne fonctionnera pas dans ne importe quelle théorie des ensembles avec le axiome de séparation); mais il ne fonctionne dans Nouvelles Fondations (et dans les systèmes connexes connus pour être conforme) et, dans certains systèmes de tapez théorie.
). Cette définition ne fonctionne pas dans les systèmes habituels de la théorie des ensembles axiomatique parce que les collections impliquées sont trop grandes (il ne fonctionnera pas dans ne importe quelle théorie des ensembles avec le axiome de séparation); mais il ne fonctionne dans Nouvelles Fondations (et dans les systèmes connexes connus pour être conforme) et, dans certains systèmes de tapez théorie.
Pour le reste de cet article, nous suivons la construction standard décrit ci-dessus.
Propriétés
On peut définir de façon récursive une addition sur des nombres naturels en éditant 0 = a + a + a et S (b) = S (a + b) pour tout a, b. Cela transforme les nombres naturels (N, +) dans un commutative Monoid avec 0 élément d'identité, la soi-disant monoïde libre avec un générateur. Ce monoid satisfait la la propriété d'annulation et peut être intégré dans un groupe . Le plus petit groupe contenant les nombres naturels sont les entiers .
Si nous définissons une: S = (0), puis b + 1 = b + S (0) = S (B + 0) = S (b). Ce est, b + 1 est tout simplement le successeur de b.
De manière analogue, étant donné que l'addition a été définie, une multiplication × peuvent être définies par une × 0 = 0 et a × S (b) = (A × B) + un. Cela transforme (N *, ×) dans un monoïde commutatif gratuit avec une élément d'identité; un groupe électrogène pour cette monoïde est l'ensemble des nombres premiers . Addition et la multiplication sont compatibles, qui se exprime dans le droit de la distribution: a × (b + c) = (a × b) + (a × c). Ces propriétés de l'addition et la multiplication des nombres naturels font une instance d'un commutative semiring. Semi-anneaux sont une généralisation algébrique des nombres naturels où la multiplication est pas nécessairement commutative.
Si nous interprétons les nombres naturels comme «l'exclusion de 0", et "à partir de 1", les définitions des + et × sont comme ci-dessus, sauf que nous commençons avec un + 1 = S (A) et une × 1 = a.
Pour le reste de l'article, nous écrivons ab pour indiquer le produit a × b, et nous ne assumons également la norme ordre des opérations.
En outre, on définit un ordre total sur les nombres naturels en écrivant un ≤ b si et seulement si il existe un autre nombre naturel avec un c + c = b. Cette commande est compatible avec les opérations arithmétiques dans le sens suivant: si a, b et c sont des nombres naturels et a ≤ b, alors a + c ≤ b + c et ac ≤ bc. Une propriété importante des nombres naturels, ce est qu'ils sont bien ordonné: chaque ensemble non vide de nombres naturels a un plus petit élément. Le rang parmi les ensembles bien ordonnés est exprimé par un nombre ordinal ; pour les nombres naturels ce est exprimé en "  ».
».
Se il est en général pas possible de diviser un nombre naturel par un autre et obtenir un nombre naturel à la suite, la procédure de division avec reste est disponible comme un substitut: pour tout deux nombres naturels a et b avec b ≠ 0, nous pouvons trouver naturelle nombres q et r de telle sorte que
- a = bq + r et r <b
Le nombre q est appelé quotient et r est appelé le reste de la division de a par b. Les nombres q et r sont déterminés de façon unique par a et b. Ceci, la algorithme de division, est essentielle pour plusieurs autres propriétés ( divisibilité ), des algorithmes (par exemple, la Algorithme d'Euclide), et des idées dans la théorie des nombres.
Les nombres naturels, y compris sous forme d'un zéro monoïde commutatif sous addition (avec élément ayant une identité zéro), et la multiplication (avec un élément d'identité).
Généralisations
Deux généralisations des nombres naturels proviennent des deux utilisations:
- Un nombre naturel peut être utilisé pour exprimer la taille d'un ensemble fini; plus généralement un nombre cardinal est une mesure de la taille d'un ensemble convient également pour des ensembles infinis; cela fait référence à une notion de "taille" de telle sorte que se il existe une bijection entre deux jeux qu'ils ont de la même taille. L'ensemble des nombres naturels lui-même et tout autre ensemble infini dénombrable a cardinalité Module: Aleph_number ( parler · · hist · · liens · sous-pages essais - résultats)
(  ).
).
- Les nombres ordinaux «premier», «deuxième», «troisième» peuvent être attribués à des éléments d'un ensemble fini totalement ordonné, et aussi pour les éléments de bien-ensembles ordonnés infini dénombrable comme l'ensemble des nombres naturels lui-même. Cela peut être généralisée à nombres ordinaux qui décrivent la position d'un élément dans un ordre établi bien en général. Un nombre ordinal est également utilisé pour décrire la «taille» d'un ensemble bien ordonné, dans un sens différent de cardinal: se il ya une isomorphisme d'ordre entre deux ensembles bien ordonnés, ils ont le même nombre ordinal. Le premier nombre ordinal qui ne est pas un nombre entier naturel est exprimée en
 ; ce est également le numéro d'ordre de l'ensemble des nombres naturels lui-même.
; ce est également le numéro d'ordre de l'ensemble des nombres naturels lui-même.
 et
et  doivent être distinguées parce que de nombreux ensembles bien ordonnés avec nombre cardinal
doivent être distinguées parce que de nombreux ensembles bien ordonnés avec nombre cardinal  avoir un numéro d'ordre plus élevé que
avoir un numéro d'ordre plus élevé que  , Par exemple,
, Par exemple, 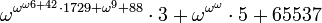 ;
;  est la valeur la plus faible possible (la ordinal initial).
est la valeur la plus faible possible (la ordinal initial).
Pour finis ensembles bien ordonnés il ya un-à-un la correspondance entre le nombre ordinal et cardinal; par conséquent, ils peuvent être exprimés à la fois par le même nombre entier naturel, le nombre d'éléments de l'ensemble. Ce nombre peut également être utilisé pour décrire la position d'un élément dans un plus grand fini ou infini, séquence .
Autres généralisations sont discutés dans l'article sur les numéros .
