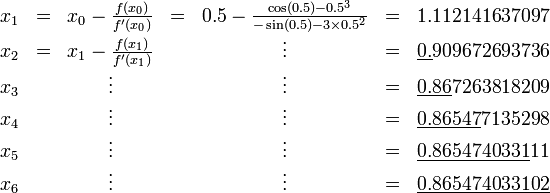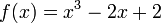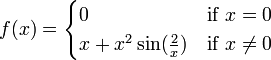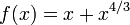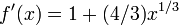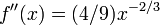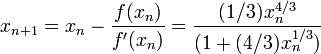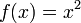La méthode de Newton

En analyse numérique, la méthode de Newton (également connu sous le nom de Newton Raphson ou la méthode de Newton-Fourier) est peut-être la meilleure méthode connue pour trouver de meilleures approximations successivement aux zéros (ou racines) d'un réel -Évaluées fonction . La méthode de Newton peut souvent convergent remarquablement rapidement, surtout si l'itération commence la racine "assez près" souhaitée. Juste comment proche "suffisamment proche" doit être et à quelle vitesse "remarquablement vite" peut être dépend du problème, comme on le verra en détail ci-dessous. Malheureusement, loin de la racine souhaitée, la méthode de Newton peut facilement conduire à un utilisateur non averti égarer et égarer avec peu d'avertissement. Ainsi, de bonnes implémentations du procédé intégrer dans une routine qui détecte également les surmonte et peut-être des échecs de convergence possibles.

La méthode de Newton peut également être utilisé pour trouver un minimum ou maximum d'une telle fonction, en trouvant un zéro dans la dérivée première de la fonction, voir La méthode de Newton comme un algorithme d'optimisation.

L'algorithme est le premier dans la classe de Les méthodes de chef de famille, réussi par Méthode de Halley.

Description de la méthode

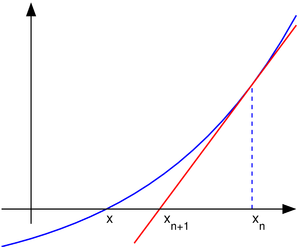
L'idée de la méthode est la suivante: on part d'une estimation initiale qui est assez proche de la vraie racine, alors la fonction est approchée par sa tangente (qui peut être calculé en utilisant les outils de calcul ), et on calcule x ordonnée à l'origine de cette tangente (qui est fait facilement avec l'algèbre élémentaire). Ce x ordonnée à l'origine sera typiquement une meilleure approximation de la racine de la fonction que l'estimation initiale, et la méthode peut être réitéré.

Une illustration d'une itération de la méthode de Newton (la fonction f est représentée en bleu et la ligne tangente est en rouge). Nous voyons que est une meilleure approximation que 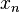pour la racine de la fonction .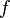

Supposons f: [a, b] → R est un différentiable fonction définie sur la intervalle [a, b] avec les valeurs dans le nombres réels R. La formule pour faire converger sur la racine peut être facilement déduite. Supposons que nous ayons un peu de courant rapprochement x _n. Ensuite, nous pouvons déduire la formule pour une meilleure approximation, x _{n + 1} en se référant au schéma sur la droite. Nous savons de la définition du dérivé à un moment donné que ce est la pente d'une tangente à ce point.

C'est

.

Ici, f 'représente la dérivée de la fonction f. Puis par l'algèbre simple nous pouvons tirer

.

Nous commençons le processus off avec une valeur initiale arbitraire x _0. (Le plus proche du zéro, mieux ce est. Mais, en l'absence de toute intuition sur l'endroit où pourrait se trouver le zéro, une «estimation et vérifier« méthode pourrait réduire les possibilités à un assez petit intervalle faisant appel à la théorème de la valeur intermédiaire.) La méthode sera généralement converger, à condition que cette supposition initiale est suffisamment proche du zéro inconnue, et que 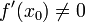. En outre, pour un zéro de une multiplicité, la convergence est au moins quadratique (voir vitesse de convergence) dans un voisinage du zéro, ce qui signifie intuitivement que le nombre de chiffres corrects au moins approximativement double de chaque étape. Plus de détails peuvent être trouvés dans la section de l'analyse ci-dessous.

Exemple

Considérons le problème de trouver le nombre positif x cos (x) = x ^3. On peut reformuler que de trouver le zéro de f (x) = cos (x) - x ^3. Nous avons f '(x) = sin (x) - 3 x ^2. Depuis cos (x) ≤ 1 pour tout x et x ^3> 1 pour x> 1, nous savons que notre zéro se situe entre 0 et 1. Nous essayons une valeur de départ de x ₀ = 0,5.

Les chiffres corrects sont soulignés dans l'exemple ci-dessus. En particulier, x ₆ est correcte au nombre de décimales donné. Nous voyons que le nombre de chiffres corrects après la virgule augmente de 2 (pour x ₃₎ à 5 et 10, illustrant la convergence quadratique.

Histoire

La méthode de Newton a été décrit par Isaac Newton à De analysi par aequationes numero terminorum infinitas (écrit en 1669, publié en 1711 par William Jones) et à De METODIS fluxionum et serierum infinitarum (écrit en 1671, traduit et publié en Fluxion en 1736 par John Colson). Cependant, sa description diffère sensiblement de la description donnée ci-dessus moderne: Newton se applique seulement à la méthode des polynômes. Il ne calcule pas les approximations successives , Mais calcule une suite de polynômes et seulement à la fin, il arrive à une approximation de la racine x. Enfin, Newton considère la méthode purement algébrique et ne remarque pas la connexion avec le calcul. Isaac Newton probablement dérivé sa méthode à partir d'une méthode similaire mais moins précise par François Viète. L'essence de la méthode de Viète peut être trouvé dans le travail de la Persique mathématicien Sharaf al-Din al-Tusi (Ypma 1995). Un cas particulier de la méthode de Newton pour calculer des racines carrées a été connu beaucoup plus tôt et est souvent appelé le Méthode babylonienne.

La méthode de Newton a été publié la première fois en 1685 dans le Traité de l'algèbre à la fois historique et pratique par John Wallis. En 1690, Joseph Raphson publié une description simplifiée Universalis Analyse de aequationum. Raphson nouveau considéré la méthode de Newton purement comme une méthode algébrique et limite son utilisation aux polynômes, mais il décrit la méthode en termes de approximations successives x _n à la place de la séquence plus complexe des polynômes utilisés par Newton. Enfin, en 1740, Thomas Simpson décrit la méthode de Newton comme une méthode itérative pour résoudre les équations non linéaires générales en utilisant le calcul fluxional, donnant essentiellement la description ci-dessus. Dans la même publication, Simpson donne également la généralisation des systèmes de deux équations et note que la méthode de Newton peut être utilisé pour résoudre des problèmes d'optimisation en réglant le gradient à zéro.

Arthur Cayley en 1879 à Le problème imaginaire Newton-Fourier a été le premier qui a remarqué les difficultés à généraliser la méthode de Newton aux racines complexes de polynômes de degré supérieur à 2 et complexes valeurs initiales. Cela a ouvert la voie à l'étude de la théorie d'itérations de fonctions rationnelles.

Considérations pratiques

En général convergence quadratique est: l'erreur est essentiellement carrée à chaque étape (ce est le nombre de chiffres exacts double à chaque étape). Il ya quelques mises en garde, cependant. Tout d'abord, la méthode de Newton nécessite que le dérivé est calculée directement. (Si l'instrument dérivé est approchée par le pente d'une droite passant par deux points sur la fonction, la sécantes résultats de la méthode; cela peut être plus efficace selon la façon dont on mesure l'effort de calcul.) Deuxièmement, si la valeur initiale est trop loin du zéro absolu, la méthode de Newton peut échouer à converger. Pour cette raison, la plupart des implémentations pratiques de la méthode de Newton mis une limite supérieure sur le nombre d'itérations et peut-être de la taille des itération. Troisièmement, si le root a recherché multiplicité supérieur à un, le taux de convergence ne est que la réduction des erreurs linéaires (par un facteur constant à chaque étape) à moins que des mesures spéciales soient prises.

Depuis la plus grave des problèmes ci-dessus est la possibilité d'une défaillance de la convergence, Press et al. (1992) présentent une version de la méthode de Newton qui commence au point milieu d'un intervalle dans lequel la racine est connue pour se trouver et se arrête l'itération si une itération est généré qui se trouve en dehors de l'intervalle.

Les développeurs de systèmes informatiques à grande échelle impliquant recherche des racines ont tendance à préférer la Procédé sécante sur la méthode de Newton, car l'utilisation d'un quotient de différence à la place du dérivé de la méthode de Newton implique que le code supplémentaire pour calculer la dérivée n'a pas besoin d'être maintenue. Dans la pratique, les avantages de maintenir une base de code plus petit emportent généralement sur les caractéristiques de convergence supérieures de la méthode de Newton.

Contre-exemples

Les tangentes de x ^ 3-2 x + 2 à 0 et une intersection de l'axe-x à 1 et 0, respectivement, illustrant pourquoi la méthode de Newton oscille entre ces valeurs pour quelques points de départ.

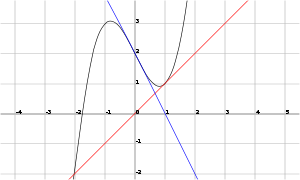
Point de départ trop loin

Si le point de départ ne est pas près d'une racine puis la convergence peut ne pas arriver. Laisser

et de prendre 0 comme point de départ. La première itération produit une seconde et les retours d'itération à 0 de sorte que la séquence va osciller entre les deux sans converger à une racine. En général, le comportement de la séquence peut être très complexe. (Voir Fractale Newton.)

Dans les exemples suivants, la racine est à zéro souhaitée pour la simplicité, il aurait pu être placé ailleurs.

Dérivée discontinue

Si le dérivé ne est pas continue à la racine, puis la convergence peut échouer à se produire dans ne importe quel quartier de la racine. Considérons la fonction

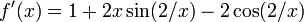Puis et ailleurs.

Dans ne importe quel quartier de la racine, ce dérivé ne cesse de changer signe que x tend vers 0 de la droite (ou à partir de la gauche), tandis que pour .

Si 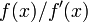ne est pas borné près de la racine et de la méthode de Newton ne convergera pas, même si: la fonction est différentiable partout; le dérivé ne est pas nulle à la racine; est infiniment dérivable sauf à la racine; et le dérivé est délimité au voisinage de la racine (contrairement à son inverse).

Aucune dérivée seconde

Si il ne est pas dérivée seconde à la racine, puis la convergence peut manquer d'être quadratique. En effet, soit

Puis

Et

excepté quand où il ne est pas définie. Donné ,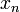

qui a environ 4/3 fois plus de bits de précision que 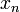a. Ce est moins que les deux fois plus nombreux qui seraient nécessaires pour la convergence quadratique. Donc, la convergence de la méthode de Newton (dans ce cas) ne est pas quadratique, même si: la fonction est continûment différentiable partout; le dérivé ne est pas nulle à la racine; et 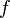est infiniment dérivable sauf à la racine souhaitée.

Dérivée nulle

Si le premier dérivé est égal à zéro à la racine, puis convergence ne sera pas quadratique. En effet, soit

Puis 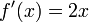et par conséquent 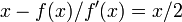. Donc, la convergence ne est pas quadratique, même si la fonction est infiniment différentiable partout.

Analyse

Supposons que la fonction f a une α à zéro, ce est-f (α) = 0.

Si f est continûment différentiable et son dérivé ne annule pas en α, alors il existe une voisinage de α tel que, pour toutes les valeurs de départ x ₀ dans ce quartier, la séquence {x _n} sera converge vers α.

Si la fonction est continûment différentiable et son dérivé ne annule pas en α et il a une dérivée seconde α puis la convergence est quadratique ou plus rapide. Si la dérivée seconde ne annule pas en α puis la convergence est simplement quadratique.

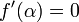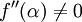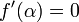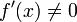Si le dérivé ne disparaît au α, alors la convergence ne est généralement linéaire. Plus précisément, si f est deux fois continûment différentiable, et , Alors il existe un voisinage de α tel que, pour toutes les valeurs de départ x ₀ dans ce quartier, la séquence d'itération converge linéairement, avec journal des taux _{de 10} 2 (Süli & Mayers, l'exercice 1.6). Alternativement, si et ailleurs, dans un voisinage U de α, α étant un zéro de r multiplicité et si 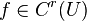alors il existe un voisinage de α tel que, pour toutes les valeurs de départ x ₀ dans ce quartier, la séquence d'itération converge linéairement.

Cependant, même la convergence linéaire ne est pas garantie dans des situations pathologiques.

En pratique, ces résultats sont local et le quartier de convergence ne sont pas connus a priori, mais il ya aussi des résultats sur la convergence mondiale, par exemple, étant donné un quartier droit U ₊ de α, si f est deux fois dérivable dans U ₊ et si 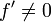, 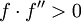à U _+, puis, pour chaque x _{0 +} U dans la séquence x _k est monotone décroissante de α.

Généralisations

Systèmes d'équations non linéaires

On peut utiliser la méthode de Newton aussi pour résoudre des systèmes de k (non linéaires) équations, ce qui revient à trouver les zéros de fonctions continûment dérivables F: R ^k → R ^k. Dans la formulation indiquée ci-dessus, on a alors laissé à multiplier par l'inverse de la k k -by- Jacobienne matrice J _F (x _n) au lieu de diviser par f '(x _n). Plutôt que de calcul fait l'inverse de cette matrice, on peut gagner du temps en résolvant le système d'équations linéaires

pour l'inconnu x _{n 1} - x _n. Encore une fois, cette méthode ne fonctionne que si la valeur initiale x ₀ est suffisamment proche de la vraie zéro. Typiquement, une région qui est bien élevé est situé d'abord avec une autre méthode et la méthode de Newton est ensuite utilisé pour "polish" une racine qui est déjà connu environ.

Équations non linéaires dans un espace de Banach

Une autre généralisation est la méthode de Newton pour trouver un zéro d'une fonction F définie dans un Espace de Banach. Dans ce cas, la formulation est

,

où 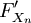est le Fréchet appliqué au point 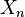. Il faut le dérivé Fréchet être inversible à chaque 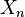pour que la méthode soit applicable.

Fonctions complexes

Bassins d'attraction pour x ^5-1 = 0; foncée signifie plus d'itérations pour converger.

Lorsqu'il se agit de fonctions complexes, toutefois, la méthode de Newton peuvent être appliqués directement à trouver leurs zéros. Pendant de nombreuses fonctions complexes, la limite de l'ensemble (également connu sous le nom bassin d'attraction) à partir de toutes les valeurs qui provoquent le procédé de converger vers zéro un particulier est une fractale .