
Significar
Informações de fundo
Este conteúdo da Wikipedia foi escolhida pela SOS Children para adequação nas escolas ao redor do mundo. Clique aqui para saber mais sobre apadrinhamento de crianças.
Em estatísticas , a média tem dois significados relacionados:
- a média aritmética (e distingue-se da ou média geométrica média harmônica).
- o valor esperado de uma variável aleatória , que também é chamado a média da população.
Às vezes é afirmado que a "média" significa média. Isso é incorreto se "dizer" é tomado no sentido específico de "aritmética" como existem diferentes tipos de médias: a média, mediana e modo . Por exemplo, os preços médios de casas quase sempre usam o valor mediano para a média.
Para um de valor real variável aleatória X, a média é a expectativa de X. Note que nem todos os distribuição de probabilidade tem uma média definida (ou variância ); ver o Distribuição Cauchy para um exemplo.
Para conjunto de dados, é a média da soma das observações dividido pelo número de observações. A média é frequentemente citado, juntamente com o desvio padrão : a média descreve a localização central dos dados, e o desvio padrão descreve a propagação.
Uma medida alternativa da dispersão é o desvio médio, equivalente à média desvio absoluto da média. Ele é menos sensível a outliers, mas menos matematicamente tratável.
Bem como estatísticas, meios são frequentemente utilizados em geometria e análise; uma vasta gama de meios têm sido desenvolvidos para estes fins, que não são muito utilizados nas estatísticas. Estes estão listados abaixo.
Exemplos de meios
Média aritmética
A média aritmética é a média "standard", muitas vezes chamado simplesmente de "dizer".
A média pode muitas vezes ser confundida com a mediana ou modo . A média é a média aritmética de um conjunto de valores, ou de distribuição; no entanto, para distribuições assimétricas, a média não é necessariamente o mesmo que o valor médio (média), ou o mais provável (modo). Por exemplo, a média de rendimento é desviado para cima por um pequeno número de pessoas com rendimentos muito grandes, de modo que a maioria têm uma renda menor do que a média. Por outro lado, o rendimento médio é o nível no qual a metade da população está abaixo e metade é acima. A renda modo é a renda mais provável, e favorece o maior número de pessoas com rendimentos mais baixos. A mediana ou moda são muitas vezes medidas mais intuitivas de tais dados.
Dito isto, muitas distribuições distorcidas são melhor descritas pelo seu significativo - como as exponenciais e Poisson distribuições.
Por exemplo, a média aritmética das 34, 27, 45, 55, 22, 34 (seis valores) é (34 + 27 + 45 + 55 + 22 + 34) / 6 = 217/6 ≈ 36,167.
A média geométrica
O média geométrica é uma média que é útil para conjuntos de números que são interpretados de acordo com o seu produto e a sua soma não (como é o caso com a média aritmética). Por exemplo, as taxas de crescimento.
Por exemplo, a média geométrica de 34, 27, 45, 55, 22, 34 (seis valores) é (34 × 27 × 45 × 55 × 22 × 34) 1/6 1/6 = 1699493400 = 34,545.
Média harmônica
O média harmónica é uma média que é útil para conjuntos de números que são definidos em relação a alguns unitária, por exemplo velocidade (distância por unidade de tempo).
Por exemplo, a média harmônica dos números 34, 27, 45, 55, 22 e 34 é
Meios generalizadas
Potência média
O média generalizada, também conhecida como a potência média ou o titular dizer, é uma abstração do quadrática, aritmética, geométrica e meios harmônicas. É definido pela
Ao escolher o valor apropriado para o parâmetro m obtemos
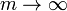 | máximo |
 | quadrático, |
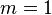 | média aritmética , |
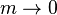 | média geométrica, |
 | harmônico dizer, |
 | mínimo. |
f-médio
Isto pode ser generalizado como ainda o generalizada f-médio
e novamente uma escolha apropriada de um invertível  darei
darei
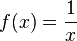 | harmônico dizer, |
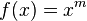 | potência média, |
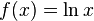 | média geométrica. |
Média aritmética ponderada
O média aritmética ponderada é utilizado, quando se quer combinar os valores médios a partir de amostras da mesma população, com diferentes tamanhos de amostra:
Os pesos  representam os limites da amostra parcial. Em outras aplicações que representam uma medida para a fiabilidade da influência sobre a média por respectivos valores.
representam os limites da amostra parcial. Em outras aplicações que representam uma medida para a fiabilidade da influência sobre a média por respectivos valores.
Média truncada
Às vezes, um conjunto de números (o dados) pode ser contaminado por valores extremos imprecisas, ou seja, valores que são demasiado baixo ou demasiado elevado. Neste caso pode-se utilizar um média truncada. Ele envolve o descarte de uma parte dos dados dada na parte superior ou na extremidade inferior, tipicamente uma quantidade igual em cada extremidade, e em seguida, tomando a média aritmética dos dados restantes. O número de valores removidos é indicado como uma percentagem do número total de valores.
Interquartil dizer
O interquartil dizer é um exemplo específico de uma média truncada. É simplesmente a média aritmética depois de remover o baixo eo mais alto trimestre de valores.
assumindo os valores foram encomendados.
A média de uma função
No cálculo , e especialmente cálculo multivariado, a média de uma função é vagamente definida como o valor médio da função ao longo do seu domínio. Em uma variável, a média de uma função f (x) ao longo do intervalo (a, b) é definido pela
(Veja também teorema do valor médio). Em diversas variáveis, a média ao longo de um relativamente compacto domínio L em um espaço euclidiano é definida pela
Isto generaliza a média aritmética. Por outro lado, também é possível generalizar a média geométrica de funções, definindo a média geométrica das f para ser
Mais geralmente, em medir a teoria ea teoria da probabilidade ou tipo de significar desempenha um papel importante. Neste contexto, Desigualdade de Jensen coloca estimativas cortantes sobre a relação entre estes dois conceitos diferentes da média de uma função.
A média dos ângulos
A maioria dos meios habituais falhar em quantidades circulares, como ângulos , daytimes, partes fracionárias de números reais . Para as quantidades que você precisa de um média de quantidades circulares.
Outros meios
- Média aritmética-geométrica
- Aritmética harmônica média
- Cesaro dizer
- Chisini média
- Média Contraharmonic
- Média simétrica Elementary
- Média geométrica harmônico
- Heinz dizer
- Média Heronian
- Identric dizer
- Mínimos quadrados dizer
- Lehmer dizer
- Média logarítmica
- Mediano
- Root mean square
- Stolarsky dizer
- Temporal média
- Geométrico médio, ponderado
- Média harmônica ponderada
- A entropia de Rényi (a generalizada f-média)
Propriedades
O método mais geral para a definição de uma média ou média, y, leva qualquer função de uma lista g (x_1, x_2, ..., x_n), que é simétrica com respeito ao permutação dos membros da lista, e compara-o ao mesmo função com o valor da média substituindo cada membro da lista: g (x_1, x_2, ..., x_n) = G (y, y, ..., y). Todos os meios de compartilhar algumas propriedades e propriedades adicionais são compartilhados pelos meios mais comuns. Algumas dessas propriedades são recolhidos aqui.
Média ponderada
A média ponderada  é uma função que mapeia tuplas de números positivos para um número positivo (
é uma função que mapeia tuplas de números positivos para um número positivo (  ).
).
- " Ponto fixo ":
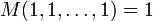
- Homogeneidade:

- (Usando notação vetorial:
 )
)
- (Usando notação vetorial:
- Monotonia:

Daqui resulta
- Boundedness:
![\ Forall x \ x H \ em [\ min x, \ max x]](../../images/135/13510.png)
- Continuidade:

- Esboço de uma prova: Porque
 e
e  segue-
segue- 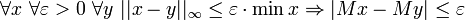 .
.
- Existem meios que não são diferenciáveis . Por exemplo, o número máximo de um tuplo é considerada um significativo (como um caso extremo do potência média, ou como um caso especial de um mediano ), mas não é diferenciável.
- Todos os meios acima listados, com a excepção de a maior parte do F-meio generalizadas, satisfazer as propriedades apresentadas.
- Se
 é bijective, em seguida, o f-média generalizada satisfaz a propriedade ponto fixo.
é bijective, em seguida, o f-média generalizada satisfaz a propriedade ponto fixo. - Se
 é estritamente monotônica, em seguida, o f-média generalizada satisfazer também a propriedade monotonia.
é estritamente monotônica, em seguida, o f-média generalizada satisfazer também a propriedade monotonia. - Em geral, uma f-média generalizada vai perder homogeneidade.
- Se
As propriedades acima implicam técnicas para construir meios mais complexos:
Se  são meios ponderados,
são meios ponderados, 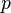 é um positivo número real , em seguida,
é um positivo número real , em seguida, 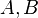 com
com
são também uma média ponderada.
Média não ponderada
Intuitivamente falado, uma média não ponderada é uma média ponderada com pesos iguais. Desde a nossa definição de média ponderada acima não expõe pesos específicos, pesos iguais deve ser afirmado por uma maneira diferente. Uma visão diferente sobre ponderação é homogêneo, que as entradas podem ser trocadas sem alterar o resultado.
Assim podemos definir  ser uma média não ponderada se é uma média ponderada e para cada permutação
ser uma média não ponderada se é uma média ponderada e para cada permutação 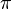 de entradas, o resultado é o mesmo. Deixar
de entradas, o resultado é o mesmo. Deixar 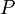 É o conjunto de permutações de
É o conjunto de permutações de  -tuples.
-tuples.
- Simetria:
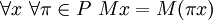
Analogamente aos meios ponderados, se 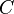 é uma média ponderada e
é uma média ponderada e  são meios não ponderadas,
são meios não ponderadas, 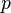 é um positivo número real , em seguida,
é um positivo número real , em seguida, 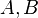 com
com
também são meios não ponderados.
Converso média não ponderada a média ponderada
Uma média não ponderada pode ser transformado em uma média ponderada por elementos repetidos. Esta ligação pode também ser utilizada para indicar que uma média ponderada é a versão de um meio não-ponderada. Digamos que você tem a média não ponderada  e peso dos números de números naturais
e peso dos números de números naturais  . (Se os números forem racionais , então multiplicá-los com o denominador comum mínimo.) Em seguida, a média ponderada correspondente
. (Se os números forem racionais , então multiplicá-los com o denominador comum mínimo.) Em seguida, a média ponderada correspondente 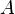 é obtido pela
é obtido pela
 .
.
Meios de tuplos de tamanhos diferentes
Se um significativo  é definido para tuplos de vários tamanhos, em seguida, uma espera igualmente que a média de um tuplo é delimitada pelos meios de partições. Mais precisamente
é definido para tuplos de vários tamanhos, em seguida, uma espera igualmente que a média de um tuplo é delimitada pelos meios de partições. Mais precisamente
- Dado uma tupla arbitrária
 , Que é particionado em
, Que é particionado em  , Então ele mantém
, Então ele mantém  . (Ver Convex hull)
. (Ver Convex hull)
Educação matemática
Em muitos padrões curriculares estaduais e governo, os alunos são tradicionalmente esperado para aprender o sentido nem fórmula para calcular a média da quarta série. No entanto, em muitos baseada em padrões, currículos de Matemática, os alunos são incentivados a inventar seus próprios métodos, e não pode ser ensinado o método tradicional. Textos da reforma com base, tais como TERC, de facto, ensina a desencorajar tradicional "adicionar os números e dividir pelo número de artigos do" método em favor de passar mais tempo no conceito de mediana , que não requer divisão. No entanto, média pode ser calculada com uma simples calculadora de quatro funções, enquanto a mediana requer um computador. O mesmo guia do professor dedica várias páginas sobre como encontrar a mediana de um conjunto, que é julgado para ser mais simples do que encontrar a média.
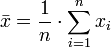

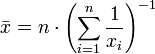



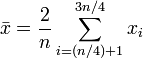

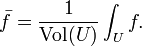
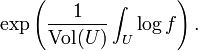
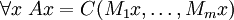
![\ Forall x \ B x = \ sqrt [p] {C (x_1 ^ p, \ dots, x_n ^ p)}](../../images/135/13518.png)
![\ Forall x \ B x = \ sqrt [p] {M_1 (x_1 ^ p, \ dots, x_n ^ p)}](../../images/135/13521.png)
