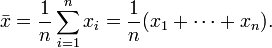Média aritmética

Em matemática e estatísticas , a aritmética média (ou simplesmente a média) de uma lista de números é a soma de todos os membros da lista, dividida pelo número de itens na lista. Se a lista é uma população estatística, em seguida a média de população que é chamado de uma média da população. Se a lista é uma amostra estatística , chamamos o resultado da estatística média da amostra.

A média é o tipo mais comumente usado de média e é muitas vezes referida apenas como a média. O termo "significa" ou "média aritmética" é preferido em matemática e estatística para distingui-lo de outros médias tais como a mediana e o modo.

Introdução

Se se designar um conjunto de dados por X = (x _1, x _2, ..., x _n), em seguida, a média da amostra é tipicamente indicado com uma barra horizontal através da variável ( 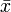, Enunciado "x bar").

O símbolo μ (em grego: mu) é utilizada para designar a média aritmética de uma população inteira. Ou, para uma número aleatório que tem uma média definida, μ é a média probabilística ou valor esperado do número aleatório. Se o conjunto X é uma coleção de números aleatórios com média probabilística de μ, em seguida, para qualquer amostra individual, x _i, a partir dessa coleção, μ = E {x} é o _i valor esperado da referida amostra.

Na prática, a diferença entre μ e 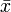é que μ é tipicamente não observável, porque se observa apenas uma amostra, em vez de toda a população, e, se a amostra é retirada aleatoriamente, em seguida, pode-se tratar 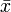, Mas não μ, como uma variável aleatória , atribuindo uma distribuição de probabilidade de que (a distribuição de amostragem da média).

Ambos são calculados da mesma maneira:

Se X é uma variável aleatória , então o valor esperado de X pode ser visto como a média aritmética de longo prazo significa que ocorre em medições repetidas de X. Este é o conteúdo do lei dos grandes números. Como resultado, a média da amostra é utilizada para estimar os valores esperados desconhecidos.

Note-se que vários outros "meios" têm sido definidos, incluindo a significativo generalizada, a generalizada f-média, o média harmônica, a aritmética-geométrica média, e vários médias ponderadas.

Exemplos

• Se você tiver 3 números, em seguida, adicioná-los e dividi-los por 3:
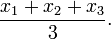
• Se você tem 4 números adicioná-los e dividir por 4:

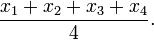
Problemas com algumas utilizações da média

Enquanto a média é muitas vezes usado para reportar tendência central, que pode não ser apropriado para descrever distribuições assimétricas, pois é facilmente mal interpretada. A média aritmética é muito influenciada por discrepantes. Estas distorções podem ocorrer quando a média é diferente da mediana. Quando isso acontece, o médio pode ser uma melhor descrição de tendência central.

Um exemplo clássico é renda média. A média aritmética pode ser mal interpretada para significar que os rendimentos da maioria das pessoas são mais elevados do que é de fato o caso. Quando apresentado com uma uma "média" pode ser levado a acreditar que os rendimentos da maioria das pessoas estão perto deste número. Este (média aritmética) de renda "média" é maior do que a renda da maioria das pessoas, porque discrepantes alta renda distorcer o resultado mais elevado (em contraste, a renda média "resiste" tal inclinação). No entanto, este "médio" não diz nada sobre o número de pessoas perto da renda mediana (nem diz nada sobre a renda modal que a maioria das pessoas estão perto). No entanto, porque pode-se relacionar descuidadamente "médios" e "a maioria das pessoas" se poderia supor incorretamente que os rendimentos da maioria das pessoas seria mais elevado (mais perto esta inflado "médio") do que são. Por exemplo, relatar a "média" patrimônio líquido em Medina, Washington como a média aritmética de todos os valores líquidos anuais renderia um número surpreendentemente elevado por causa de Bill Gates . Considere as contagens (1, 2, 2, 2, 3, 9). A média aritmética é 3,17, mas cinco das seis pontuações estão abaixo deste.

Em certas situações, a média aritmética é a medida da tendência central errado completamente. Por exemplo, se um estoque caiu 10% no primeiro ano, e subiu 30% no segundo ano, então seria incorreto para relatar o seu aumento "média" por ano durante este período de dois anos como a média aritmética (-10% + 30%) / 2 = 10%; a média correto neste caso é o média geométrica que rende um aumento médio por ano de apenas 8,2%. A razão para isto é que cada uma dessas percentagens têm diferentes pontos de partida. Se o estoque começa em US $ 30 e cai 10%, é agora em US $ 27. Se o estoque em seguida, sobe 30%, é agora US $ 35.1. A média aritmética desses aumentos é de 10%, mas desde que o estoque subiu 5,1 dólares em 2 anos, uma média de 8,2% poderia resultar na final 35,1 $ figura [$ 30 (1-10%) (1 + 30%) $ 30 = (1 + 8,2%) (1 + 8,2%) = 35,1 $]. Se usada a média aritmética de 10% da mesma maneira, não iria ficar o aumento real [$ 30 (1 + 10%) (1 + 10%) = $ 36,3].

Um cuidado especial deve ser tomado quando usando dados cíclicos, tais como fases ou ângulos. Tomando a média aritmética de um grau de 359 graus e dá um resultado de 180 graus, ao passo que 1 e 359 são ambos adjacente a 360 graus, que pode ser um valor médio mais correcta. Na aplicação geral tal supervisão conduzirá ao valor de média móvel artificialmente para o meio da gama numérica. Uma solução para este problema é a utilização da formulação optimização, e redefinir a diferença como uma distância modular.