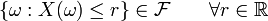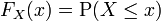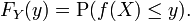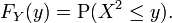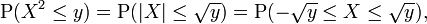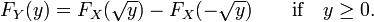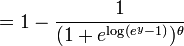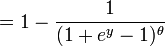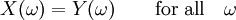Variável aleatória

Assuntos Relacionados: Matemática

Sobre este escolas selecção Wikipedia

SOS acredita que a educação dá uma chance melhor na vida de crianças no mundo em desenvolvimento também. Para comparar instituições de caridade de patrocínio esta é a melhor ligação de patrocínio .

Uma variável aleatória é uma abstração do conceito intuitivo de oportunidade de penetrar nos domínios teóricos de matemática, formando as bases da teoria da probabilidade e estatística matemática.

A teoria e linguagem de variáveis aleatórias foram formalizados ao longo dos últimos séculos ao lado de idéias de probabilidade. Familiaridade completa com todas as propriedades de variáveis aleatórias requer uma sólida formação em conceitos mais recentemente desenvolvidos da teoria da medida, mas variáveis aleatórias pode ser entendido intuitivamente em vários níveis de fluência matemática; a teoria dos conjuntos e cálculo são fundamentais.

Em termos gerais, uma variável aleatória é definida como uma quantidade cujos valores são aleatórios e que uma distribuição de probabilidade é atribuído. Mais formalmente, uma variável aleatória é uma a partir de uma função mensurável espaço para a amostra espaço mensurável de possíveis valores da variável. A definição formal de variáveis aleatórias coloca experimentos envolvendo resultados de valor real firmemente dentro do medir-quadro teórico e nos permite construir funções de distribuição de variáveis aleatórias de valor real.

Exemplos

Uma variável aleatória pode ser usado para descrever o processo de rolar uma feira morrer e os possíveis resultados {1, 2, 3, 4, 5, 6}. A representação mais óbvia é a de tomar esse conjunto como o espaço de amostragem, o medida de probabilidade para ser medida uniforme, e a função de ser o função identidade.

Para um sorteio, um espaço adequado de resultados possíveis é Ω = {H, T} (para as cabeças e caudas). Uma variável aleatória exemplo neste espaço é

$X (\ omega) = \ begin {cases} 3, e \ text {if} \ omega = \ texttt {H}, \\ -5, e \ text {if} \ omega = \ texttt {T}. \ End {} casos$

Variáveis aleatórias com valor de reais

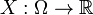Tipicamente, o espaço mensurável é o espaço mensurável sobre os números reais. Neste caso, deixa $(\ Omega, \ mathcal {F}, P)$ ser um espaço de probabilidade . Em seguida, a função $X: \ Omega \ rightarrow \ mathbb {R}$ é uma variável aleatória real se

$\ {\ Omega: X (\ omega) \ le r \} \ in \ mathcal {F} \ qquad \ forall r \ in \ mathbb {R}$

Funções de distribuição de variáveis aleatórias

Associar uma função de distribuição cumulativa (CDF) com uma variável aleatória é uma generalização da atribuição de um valor a uma variável. Se o CDF é um (contínua à direita) Função de passo Heaviside, em seguida, a variável assume o valor no salto com probabilidade 1. Em geral, o CDF especifica a probabilidade de que a variável assume valores particulares.

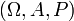Se uma variável aleatória $X: \ Omega \ to \ mathbb {R}$ definido no espaço de probabilidade $(\ Omega, A, P)$ é dada, podemos fazer perguntas como "Qual é a probabilidade de que o valor de $X$ é maior do que 2? ". Esta é a mesma que a probabilidade do evento $\ {S \ in \ Omega: X (s)> 2 \}$ que muitas vezes é escrito como $P (X> 2)$ para breve.

Gravação de todas estas probabilidades de intervalos de uma variável aleatória X de valor real de saída produz a distribuição de probabilidade de X. A distribuição de probabilidade "esquece" sobre o espaço de probabilidade particular usado para definir X e registra apenas as probabilidades de vários valores de X. Tal distribuição de probabilidade pode sempre ser capturada pelas suas função de distribuição cumulativa

$F_X (x) = \ operatorname {P} (X \ le x)$

e, por vezes, também usando um função densidade de probabilidade. Em termos medem-teórica, usamos a variável aleatória X para "empurrar para a frente" a medida P em Ω para uma medida d F em R. O espaço de probabilidade subjacente Ω é um dispositivo técnico usado para garantir a existência de variáveis aleatórias, e às vezes para construí-los. Na prática, muitas vezes um dispõe do espaço Ω completamente e apenas coloca uma medida em R que atribui medida 1 para toda a linha real, isto é, trabalha-se com distribuições de probabilidades em vez de variáveis aleatórias.

Momentos

A distribuição de probabilidade de uma variável aleatória é frequentemente caracterizado por um número reduzido de parâmetros, que também tem uma interpretação prática. Por exemplo, muitas vezes é o suficiente para saber o que o seu "valor médio" é. Este é capturado pelo conceito matemático de valor esperado de uma variável aleatória, denotado E [X]. Em geral, E [f (X)] não é igual a f (E [X]). Uma vez que o "valor médio" é conhecido, pode-se então perguntar como longe deste valor médio dos valores de X são tipicamente, uma pergunta que é respondida pela variância e desvio padrão de uma variável aleatória.

Matematicamente, isto é conhecido como o (generalizada) problema de momentos: para uma dada classe de variáveis aleatórias x, encontrar um conjunto _{i} f funções de tal modo que a expectativa de valores de E [f _i (X)] caracterizar completamente a distribuição da variável aleatória X.

Funções de variáveis aleatórias

Se temos uma variável aleatória X em Ω e uma função mensurável f: R → R, então Y = f (X) também irá ser uma variável aleatória em Ω, uma vez que a composição de funções mensuráveis também é mensurável. O mesmo procedimento que permitiu que um para ir de um espaço de probabilidade (Ω, P) para (R, DF _X) pode ser usado para obter a distribuição de Y. O função de distribuição cumulativa de Y é

$F_Y (y) = \ operatorname {P} (f (x) \ le y).$

Exemplo 1

Seja X um de valor real, variável aleatória contínua e seja Y = X ^2. Em seguida,

$F_Y (y) = \ operatorname {} P (X ^ 2 \ le y).$

Se y <0, então P ^(X2 ≤ y) = 0, então

$F_Y (y) = 0 \ qquad \ hbox {if} \ quad y <0.$

Se y ≥ 0, então

$\ Operatorname {} P (X ^ 2 \ le y) = \ operatorname {} P (| X | \ le \ sqrt {y}) = \ operatorname {} P (- \ sqrt {y} \ le X \ le \ sqrt {y}),$

assim

$F_Y (y) = F_X (\ sqrt {y}) - F_X (- \ sqrt {y}) \ qquad \ hbox {if} \ quad y \ ge 0.$

Exemplo 2

Supor $\ Scriptstyle X$ é uma variável aleatória, com uma distribuição cumulativa

$F_ {X} (x) = P (X \ leq x) = \ frac {1} {(1 + e ^ {- x}) ^ {\ theta}}$

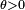onde $\ Scriptstyle \ theta> 0$ é um parâmetro fixo. Considere a variável aleatória $\ Scriptstyle Y = \ mathrm {} log (1 + e ^ {- X}).$ Em seguida,

$F_ {Y} (y) = P (Y \ leq y) = P (\ mathrm {} log (1 + e ^ {- X}) \ leq y) = P (X> - \ mathrm {} login (e ^ {y} -. 1)) \,$

A última expressão pode ser calculada em termos da distribuição cumulativa de 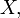$X,$ assim

$F_ {Y} (y) = 1 - F_ {X} (- \ mathrm {} login (e ^ {y} - 1)) \,$

$= 1 - \ frac {1} {(1 + e ^ {\ mathrm {} login (e ^ {y} - 1)}) ^ {\ theta}}$

$= 1 - \ frac {1} {(1 + e ^ {y} - 1) ^ {\ theta}}$

$= 1 - e ^ {- y \ theta} \,.$

Equivalência de variáveis aleatórias

Existem vários sentidos diferentes em que as variáveis aleatórias podem ser considerados equivalentes. Duas variáveis aleatórias podem ser iguais, iguais quase com certeza, iguais em média ou iguais em distribuição.

Em ordem crescente de força, a definição precisa destas noções de equivalência é dada abaixo.

A igualdade na distribuição

Duas variáveis aleatórias X e Y são iguais em distribuição se eles têm as mesmas funções de distribuição:

$\ Operatorname {} P (X \ le x) = \ operatorname {} P (Y \ le x) \ quad \ hbox {para todo} \ quad x.$

Duas variáveis aleatórias que têm igual funções geradoras de momentos têm a mesma distribuição. Isto proporciona, por exemplo, um método útil de se verificar a igualdade de certas funções de iidrv de.

Para ser iguais em distribuição, variáveis aleatórias não precisam de ser definidos no mesmo espaço de probabilidade. A noção de equivalência de distribuição é associada à seguinte noção de distância entre distribuições de probabilidade,

$d (X, Y) = \ sup_x | \ operatorname {P} (X \ le x) - \ operatorname {P} (Y \ le x) |,$

que é a base do Teste de Kolmogorov-Smirnov.

Igualdade na média

Duas variáveis aleatórias X e Y são iguais em p-th dizer se o p th momento de | X - Y | é zero, isto é,

$\ Operatorname {E} (| X-Y | ^ p) = 0.$

Igualdade no p th média implica igualdade em q th média para todos q <p. Tal como no caso anterior, existe uma distância relacionada entre as variáveis aleatórias, nomeadamente

$D_P (X, Y) = \ operatorname {E} (| X-Y | ^ p).$

Quase certeza igualdade

Duas variáveis aleatórias X e Y são iguais quase certamente se, e apenas se, a probabilidade de que eles são diferentes de zero é:

$\ Operatorname {P} (X \ neq Y) = 0.$

Para todos os efeitos práticos da teoria da probabilidade, esta noção de equivalência é tão forte quanto a igualdade real. Ela está associada à distância seguinte:

$d_ \ infty (X, Y) = \ sup_ \ omega | X (\ omega) -Y (\ omega) |,$

onde 'sup' representa neste caso o supremum essencial no sentido de teoria da medida.

Igualdade

Finalmente, as duas variáveis aleatórias X e Y são iguais se eles são iguais como funções no seu espaço de probabilidades, isto é,

$X (\ omega) = Y (\ omega) \ qquad \ hbox {para todo} \ quad \ omega$

Convergência

Grande parte da estatística matemática consiste em provar resultados de convergência para determinadas sequências de variáveis aleatórias; ver por exemplo o lei dos grandes números ea teorema do limite central.

Existem vários sentidos, em que uma sequência _(Xn) de variáveis aleatórias podem convergir para uma variável aleatória X. Estes são explicados no artigo sobre Convergência de variáveis aleatórias.

Literatura

Kallenberg, O., medidas aleatórias, 4ª edição. Academic Press, Nova Iorque, Londres; Akademie-Verlag, Berlim (1986). MR0854102 ISBN 0123949602
Papoulis, Athanasios 1965 Probabilidade, variáveis aleatórias e processos estocásticos. McGraw-Hill Kogakusha, Tóquio, 9ª edição, ISBN 0-07-119981-0.

Retirado de " http://en.wikipedia.org/w/index.php?title=Random_variable&oldid=195646641 "