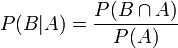Espaço de probabilidade

Assuntos Relacionados: Matemática

Fundo para as escolas Wikipédia

Esta seleção Escolas foi originalmente escolhido pelo SOS Children para as escolas no mundo em desenvolvimento sem acesso à internet. Ele está disponível como um download intranet. Veja http://www.soschildren.org/sponsor-a-child para saber mais sobre apadrinhamento de crianças.

A definição do espaço de probabilidade é o fundamento da teoria da probabilidade . Foi introduzido por Kolmogorov na 1930. Para uma alternativa algébrica para a abordagem de Kolmogorov, consulte álgebra de variáveis aleatórias.

Definição

Um espaço de probabilidade 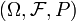$(\ Omega, \ mathcal F, P)$ é um espaço medida com uma medida P que satisfaça a axiomas de probabilidade.

O espaço amostral $\ Omega,$ é um não-vazia conjunto cujos elementos são conhecidos como os resultados ou estados de natureza e muitas vezes são dadas o símbolo 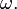$\ Omega.$ O conjunto de todos os possíveis resultados de um experimento é conhecido como o espaço amostral do experimento.

Eventos

O segundo item, $\ Mathcal F$ , É uma σ-álgebra de subconjuntos de $\ Omega$ . Seus elementos são chamados eventos, que são conjuntos de resultados para a qual se pode pedir uma probabilidade.

Porque $\ Mathcal F$ é uma σ-álgebra, ele contém $\ Omega$ ; também, o complemento de qualquer evento é um evento, ea união de qualquer sequência (finito ou infinito contável) de eventos é um evento.

Normalmente, os eventos são o Lebesgue mensurável ou Conjuntos de Borel mensuráveis de números reais.

Medida de probabilidade

A medida de probabilidade 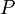$P$ é uma função de $\ Mathcal F$ aos números reais que atribui a cada evento de uma probabilidade de entre 0 e 1. Deve satisfazer o axiomas de probabilidade.

Porque 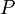$P$ é uma função definida na $\ Mathcal F$ e não sobre $\ Omega$ , O conjunto de eventos não é obrigado a ser a completa poder definir o espaço de amostra; ou seja, nem todo conjunto de resultados é necessariamente um evento.

Quando mais de uma medida está em discussão, medidas de probabilidade são muitas vezes escritos em negro negrito para distingui-los. Quando há apenas uma medida de probabilidade em discussão, é muitas vezes designado por Pr, significando "probabilidade de".

Conceitos Relacionados

Distribuição de probabilidade

Qualquer distribuição de probabilidade define uma medida de probabilidade.

Variáveis aleatórias

Uma variável aleatória X é um função mensurável do espaço amostral $\ Omega$ ; para outro espaço mensurável chamado o espaço de estado.

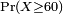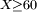Se X é um com valor de reais variável aleatória, então a notação ${\ Scriptstyle \ Pr (X \ geq 60)}$ é uma abreviação para ${\ Scriptstyle \ Pr (\ {\ omega \ in \ Omega \ mid X (\ omega) \ geq 60 \})}$ , Assumindo que ${\ Scriptstyle X \ geq 60}$ é um evento.

Probabilidade condicional

Definição de espaços de probabilidade de Kolmogorov dá origem ao conceito natural de probabilidade condicional. Cada conjunto 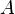$A$ com probabilidade não nula (isto é, P (a) 0>) define uma outra medida de probabilidade

$P (B \ vert A) = {P (B \ cap A) \ over P (A)}$

no espaço. Isso geralmente é lido como a "probabilidade de B dado A".

Independência

Dois eventos, A e B são considerados independente se P (A ∩ B) P = (A) P (B).

Duas variáveis aleatórias, X e Y, são considerados independentes se qualquer caso definido em termos de X é independente de qualquer evento definido em termos de Y. Formalmente, eles geram σ-álgebra independente, onde dois σ-álgebra G e H, que são subconjuntos de M são considerados independentes se qualquer elemento de G é independente de qualquer elemento de H.

O conceito de independência é o lugar onde a teoria da probabilidade afasta teoria da medida.

Exclusividade mútua

Dois eventos, A e B são considerados mutuamente exclusivos ou disjuntos se P (A ∩ B) = 0. (Isto é mais fraca do que a A ∩ B = ∅, o que é a definição de disjuntos para conjuntos).

Se A e B são eventos disjuntos, então P (A ∪ B) P = (A) + P (B). Isso se estende a uma sequência (finito ou infinito contável) de eventos. No entanto, a probabilidade de a união de um conjunto incontável de eventos não é a soma de suas probabilidades. Por exemplo, se Z é um normalmente distribuídos variável aleatória, então P (Z = X) é 0 por quaisquer x, mas P (Z é verdadeiro) = 1.

O evento A ∩ B é referida como A e B, e o evento A ∪ B como A ou B.

Exemplos

Primeiro exemplo

Se o espaço diz respeito a uma tampa de uma moeda justa, em seguida, os resultados são cabeças e caudas:

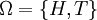
$\ Omega = \ {H, T \}$

Os eventos são

{H}: cabeças,
{T}: caudas,
{}: Nem chefes nem caudas, e
{H, T}: cara ou coroa.

Assim, 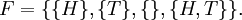$F = \ {\ H {\}, \ {T \}, \ {\}, \ {H, T \} \}.$

Há uma chance de cinquenta por cento de jogar cara ou cauda: P ({H}) = P ({T}) = 0,5. A chance de jogar nem é zero: P ({}) = 0, ea chance de jogar um ou outro é uma só: P ({H, T}) = 1.

Segundo exemplo

Se 100 eleitores serão sorteados aleatoriamente dentre todos os eleitores da Califórnia e perguntou quem eles vão votar para governador, em seguida, o conjunto de todas as sequências de 100 californianos de votos seria o espaço amostral Ω.

O conjunto de todas as sequências de 100 eleitores californianos em que pelo menos 60 votarão para Schwarzenegger é identificado com o "evento" que pelo menos 60 dos 100 eleitores escolhidos de modo votar.

Em seguida, $\ Mathcal F$ contém: (1) o conjunto de todas as sequências de 100 em que pelo menos 60 votos para Schwarzenegger; (2) o conjunto de todas as sequências de 100 em menos de 60 votos para Schwarzenegger (o inverso de (1)); (3) a amostra espaço Ω como acima; e (4) o conjunto vazio.

Um exemplo de uma variável aleatória é o número de eleitores que votarão em Schwarzenegger na amostra de 100.

Retirado de " http://en.wikipedia.org/w/index.php?title=Probability_space&oldid=194428580 "