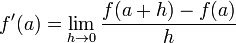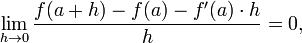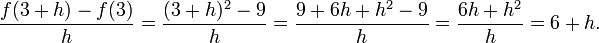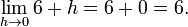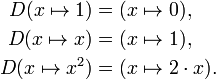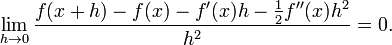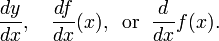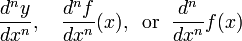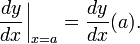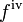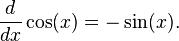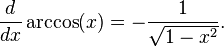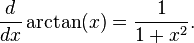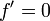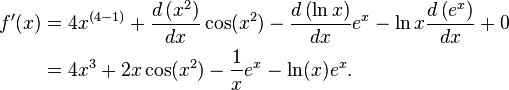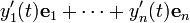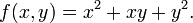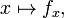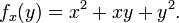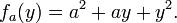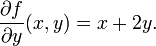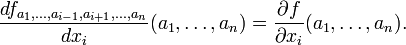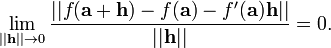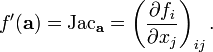Derivado

O gráfico de uma função, desenhadas em preto, e uma linha tangente a essa função, elaborado em vermelho. A inclinação da linha tangente é igual a derivada da função no ponto marcado.

No cálculo , um ramo da matemática , o derivado é uma medida de como uma função muda quando os valores de suas entradas mudar. Genericamente falando, um derivado pode ser pensada como a quantidade de uma quantidade está a mudar em algum ponto dado. Por exemplo, o derivado da posição ou distância de um carro, em algum ponto no tempo, é a velocidade instantânea, ou a velocidade instantânea (respectivamente), em que o veículo está a viajar (inversamente o integrante da velocidade é a posição do carro).

Uma noção estreitamente relacionado é o diferencial de uma função.

A derivada de uma função em um valor de entrada escolhida descreve o melhor aproximação linear da função de perto esse valor de entrada. Para função real de uma única variável real, a derivada num ponto equivale a inclinação da linha tangente à gráfico da função naquele ponto. Em dimensões superiores, a derivada de uma função num ponto é uma transformação linear chamada linearização ..

O processo de encontrar um derivado é chamado diferenciação. O teorema fundamental do cálculo afirma que a diferenciação é o processo inverso para a integração .

Diferenciação e o derivado

Em cada ponto, o derivado é a declive de um A linha que é tangente à curva . A linha vermelha é sempre tangente à curva azul; a sua inclinação é o derivado.

A diferenciação é um método para calcular a velocidade a que uma quantidade, y, as alterações em relação à mudança de uma outra quantidade, x, na qual ela é dependente. Esta taxa de variação é chamada a derivada de y em relação a x. Em linguagem mais precisa, a dependência de y sobre x significa que y é uma função de x. Se x e y são números reais , e se o gráfico de y é representada em função x, as medidas derivadas dos declive deste gráfico em cada ponto. Esta relação funcional é frequentemente denotado y = f (x), em que f representa a função.

O caso mais simples é quando Y é um função linear de x, o que significa que o gráfico de y contra x é uma linha recta. Neste caso, y = f (x) = M x + c, para os números reais m e C, e a inclinação m é dada pela

onde o símbolo Δ (a forma maiúscula da letra grega Delta) é uma abreviação de "mudança de". Esta fórmula é verdade porque

y + Δ y = f (x + Δ x) = M (x + Δ x) + c = m x + c + m Δ x = y + x m Δ.

Daqui resulta que Δ y = m Δ x.

Isto dá um valor exato para a inclinação de uma linha reta. Se a função F não é linear (isto é, o gráfico não é uma linha recta), no entanto, a alteração em y dividida pela mudança em x varia: diferenciação é um método para encontrar um valor exacto para esta taxa de variação em qualquer dado valor de x.

Figura 1. A tangente linha em (x, f (x))

Figura 2. O secante a curva y = f (x) definido nos pontos (x, f (x)) e (x + H, f (x + H)).

Figura 3. A linha tangente como limite de secantes.

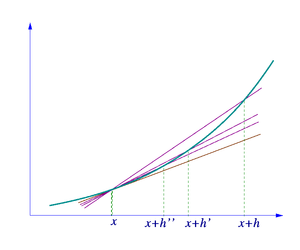
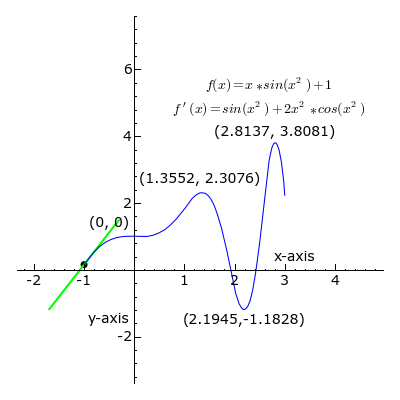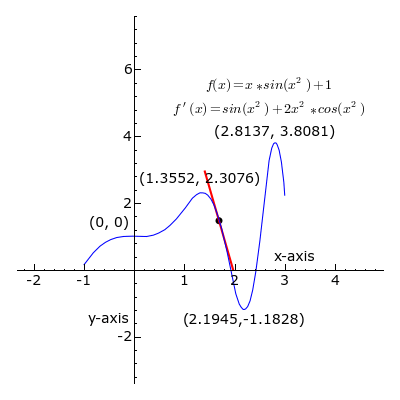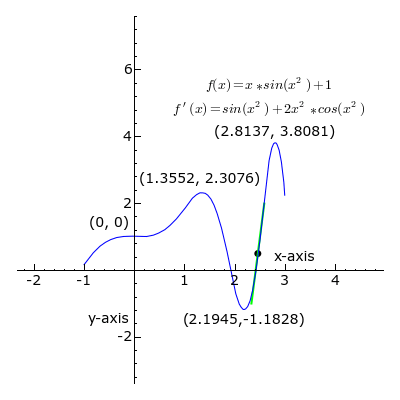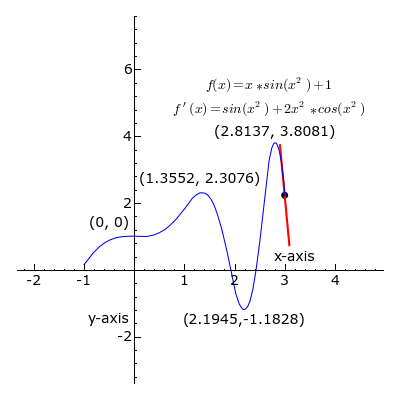
A ideia, ilustrada pelas Figuras 1-3, é para calcular a taxa de variação do valor limite do relação das diferenças Δ y / x Δ como Δ x torna-se infinitamente pequena.

Em Notação de Leibniz, tal variação infinitesimal em x é denotada por dx, e o derivado de y em relação a x é escrito

sugerindo que a razão de duas quantidades infinitesimais. (A expressão acima é pronunciado de várias maneiras, tais como "dy por dx" ou "dy sobre dx". A fase oral do formulário "dydx" é usado frequentemente em tom de conversa, embora possa levar a confusão.)

A abordagem mais comum para transformar esta idéia intuitiva para uma definição precisa usa limites , mas existem outros métodos, tais como análise não-padrão.

Definição via diferença quocientes

Seja y = f (x) seja uma função de x. Em geometria clássica, a linha tangente em um número real foi a uma única linha que passa pelo ponto (a, f (a)) que não preencheu o gráfico de f transversalmente, o que significa que a linha não passou em linha reta através do gráfico. O derivado de y em relação a x em que a é, geometricamente, a inclinação da linha tangente à curva de f em um. A inclinação da linha tangente é muito perto do declive da linha de passagem (a, f (A)) e um ponto próximo do gráfico, por exemplo, (A + H, f (A + H)). Estas linhas são chamadas linhas secantes. Um valor de h próximo de zero vai dar uma boa aproximação para a inclinação da linha tangente, e valores menores (em valor absoluto ) de h, em geral, dar uma melhor aproximações. O declive da linha secante é a diferença entre os valores de y destes pontos, dividida pela diferença entre os valores de x, ou seja,

Esta expressão é Newton 's quociente de diferença. O derivado é o valor do quociente de diferença como as linhas secantes se aproximar e mais perto da linha tangente. Formalmente, a derivada da função f em que a é o limite

do quociente de diferença como h se aproxima de zero, se esse limite existe. Se o limite existe, então f é diferenciável em um. Aqui f '(a) é uma das várias notações comuns para o derivado ( ver abaixo ).

De forma equivalente, o derivado satisfaz a propriedade de que

que tem a interpretação intuitiva (ver Figura 1) que a linha tangente à f em um dá o melhor aproximação linear

a f perto de um (ou seja, para pequenas h). Esta interpretação é a mais fácil de generalizar a outras configurações ( veja abaixo ).

Substituindo 0 para h nas causas diferença quociente divisão por zero, de modo que a inclinação da linha tangente não pode ser encontrada directamente. Em vez disso, definir Q (h) ser o quociente de diferença como uma função de h:

.

Q (h) é a inclinação da linha secante entre (a, f (A)) e (A + H, f (A + H)). Se f for um função contínua, o que significa que seu gráfico é uma curva contínua, sem lacunas, Q é uma função contínua de distância do ponto h = 0. Se o limite 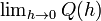existe, o que significa que existe um modo de escolha de um valor de Q (0), que faz com que o gráfico de Q uma função contínua, em seguida, a função F é diferenciável no ponto A, e o seu derivado a uma Q é igual a (0).

Na prática, a continuidade da diferença coeficiente Q (h) a h = 0 é mostrada, modificando o numerador para cancelar h no denominador. Este processo pode ser longo e tedioso para funções complicadas, e diversos cortes curtos são comumente usados para simplificar o processo.

Exemplo

A função quadrática f (x) = x ² é diferenciável em x = 3, e sua derivada existe 6. Isso é comprovado por escrever o quociente diferença da seguinte forma:

Então, temos a função simplificada no limite:

A última expressão mostra que o quociente diferença é igual a 6 + h quando h não é zero e é indefinido quando h é zero. (Recordar que, devido à definição do quociente de diferença, o quociente de diferença é sempre indefinido, quando h é igual a zero.) Porém, não é uma forma natural de preenchimento de um valor para o quociente diferença em zero, ou seja, 6. Por isso, o declive do gráfico da função quadrática no ponto (3, 9) é de 6, e assim o seu derivado em x = 3 é f (3) = 6.

Mais geralmente, um cálculo semelhante mostra que a derivada da função quadrática em x = a é f '(a) = 2 um.

Continuidade e diferenciabilidade

Esta função não tem um derivado no ponto marcado, tal como a função não é contínuo não.

Se y = f (x) é diferenciável em uma, em seguida, f deve também ser contínua a uma. Como exemplo, escolher um ponto e deixar um f ser o passo que a função retorna um valor de, digamos 1, para todos os x menor do que um, e retorna um valor diferente, digamos 10, para todos os x maior ou igual a um. f não pode ter um derivado em um. Se H for negativo, então a + h é na parte de baixo do passo, para que a linha secante a partir de um para um H + será muito íngreme, e quando h tende para zero a inclinação tende ao infinito. Se H for positiva, então a + h é na parte alta do passo, para que a linha secante a partir de um para um H + terá inclinação zero. Consequentemente, as linhas secantes não abordar qualquer inclinação única, então o limite do quociente de diferença não existe.

A função de valor absoluto é contínuo, mas deixa de ser diferenciável em x = 0, uma vez que tem uma curva fechada.

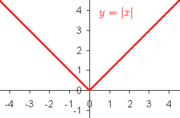
No entanto, mesmo se uma função é contínua num ponto, pode não ser diferenciável lá. Por exemplo, o valor absoluto da função y = | x | é contínua em x = 0, mas não é diferenciável lá. Se H for positiva, então a inclinação da secante entre 0 e h é um, ao passo que se h é negativo, então o declive da linha secante entre 0 e h é um negativo. Isto pode ser visto graficamente como uma "dobra" no gráfico em x = 0. Mesmo uma função com um gráfico liso não é diferenciável num ponto em que a sua tangente é vertical: Por exemplo, a função y = ³ x √ não é diferenciável em x = 0.

A maioria das funções que ocorrem na prática tem derivados em todos os pontos ou a quase todos os pontos. No entanto, um resultado de Stefan Banach afirma que o conjunto de funções que têm um derivado em algum ponto é um set escasso no espaço de todas as funções contínuas. Informalmente, isso significa que funções diferenciáveis são muito atípica entre funções contínuas. O primeiro exemplo conhecido de uma função que é contínua em todos os lugares, mas em nenhuma parte diferenciável é o Função de Weierstrass.

O derivado como uma função

Seja f uma função que tem derivada em cada ponto um no domínio de f. Porque tem um ponto de cada um derivado, não é uma função que envia o ponto A do derivado de f a uma. Esta função é escrito f (x) e é chamada de função derivado ou o derivado de f. O derivado de f recolhe todos os derivados de f em todos os pontos do domínio de f.

Às vezes um derivado de f tem a maioria, mas não todos, os pontos do seu domínio. A função cujo valor é igual a um f '(a) quando f' (a) é definida em outras posições e é indefinido é também chamado o derivado de f. É ainda uma função, mas o seu domínio é estritamente menor que o domínio de f.

Usando essa idéia, a diferenciação se torna uma função de funções: A derivada é uma operador cujo domínio é o conjunto de todas as funções que possuem derivadas em todos os pontos de seu domínio e cujo alcance é um conjunto de funções. Se se designar por este operador D, então D (f) é a função f (x). Desde D (f) é uma função, que pode ser avaliada em um ponto a. Pela definição da função derivada, D (f) (a) = f '(a).

Para efeito de comparação, considere a função de duplicação f (x) = x 2; f é uma função real de um número real, o que significa que é preciso números como entradas e tem números como saídas:

O operador D, no entanto, não é definido em números individuais. Isso só é definido em funções:

Uma vez que a saída de D é uma função, a saída de D pode ser avaliada em um ponto. Por exemplo, quando D é aplicado à função quadrática,

D gera a função de duplicação,

a qual chamamos de f (x). Esta função de saída pode, em seguida, ser avaliados para obter F (1) = 2, f (2) = 4, e assim por diante.

Derivados superiores

Seja f uma função diferenciável, e seja f '(x) o seu derivado. O derivado de f (x) (se houver) é escrito f '' (x) e é chamado o segundo derivado de f. Do mesmo modo, o derivado de uma segunda derivada, se existir, é escrito f '' '(x) e é chamado o terceiro derivado de f. Estes derivados repetidos são chamados derivados de ordem superior.

Uma função não necessita de ter f um derivado, por exemplo, se ele não é contínuo. Da mesma forma, mesmo que F tem um derivado, não pode ter uma segunda derivada. Por exemplo, deixe-

.

Um cálculo elementar mostra que f é uma função diferenciável cuja derivada é

.

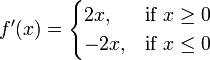f (x) é duas vezes a função de valor absoluto, e que não têm um derivado em zero. Exemplos semelhantes mostram que uma função pode ter derivados de K para qualquer número inteiro k não-negativa, mas não (k + 1) -order derivado. Uma função que tem k derivados sucessivas é chamado k vezes diferenciável. Se além disso, o derivado de k-ésima é contínuo, então a função é dito ser de diferenciabilidade classe C ^k. (Esta é uma condição mais forte do que ter derivados k. Para um exemplo, ver classe diferenciabilidade.) Uma função que tem infinitamente muitos derivados é chamado infinitamente diferenciável ou lisa.

Na linha de reais, cada função polinomial é infinitamente diferenciável. Por padrão regras de diferenciação, se um polinômio de grau n é diferenciado n vezes, então torna-se um função constante. Todos os seus derivados subsequentes são identicamente zero. Em particular, existem, por isso polinómios são funções suaves.

As derivadas de uma função f no ponto x fornecem aproximações polinomiais para essa função próximo x. Por exemplo, se f é duas vezes diferenciável, então

no sentido de que

Se f é infinitamente diferenciável, então este é o início da série de Taylor para f.

Notações para a diferenciação

Notação de Leibniz

A notação para derivados introduzidas por Gottfried Leibniz é um dos mais antigos. Ainda é geralmente usado quando a equação y = f (x) é visto como uma relação funcional entre variáveis dependentes e independentes. Em seguida, o primeiro é designado por derivado

Derivados mais elevados são expressos usando a notação

para a n-ésima derivada de y = f (x) (em relação a x).

Com a notação de Leibniz, podemos escrever a derivada de y no ponto x = a de duas maneiras diferentes:

Notação de Leibniz permite especificar a variável de diferenciação (no denominador). Isto é especialmente relevante para diferenciação parcial. Ele também faz o regra da cadeia fácil de lembrar:

Notação de Lagrange

Uma das notações modernas mais comuns para a diferenciação é devido a Joseph Louis Lagrange e utiliza o marca privilegiada, f de modo a que o derivado de uma função f (x) é denotada '(x) ou simplesmente f'. De modo semelhante, as segunda e terceira derivados são denotados

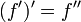e

Além deste ponto, alguns autores usam algarismos romanos, tais como

para o quarto derivado, ao passo que outros autores colocam o número de derivados em parênteses:

Esta última notação generaliza para produzir a notação f ⁽ⁿ⁾ para o n º derivada de f - esta notação é mais útil quando queremos falar sobre o derivado como sendo uma função em si, como neste caso a notação de Leibniz pode tornar-se complicada.

Notação de Newton

Notação de Newton para a diferenciação, também chamado de notação de ponto, coloca um ponto sobre o nome da função de representar um derivado. Se y = f (t), então

e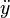

denotam, respectivamente, as primeira e segunda derivadas de Y em relação a t. Esta notação é usado quase exclusivamente para derivados de tempo, o que significa que a variável independente da função representa tempo . É muito comum em física e em disciplinas matemáticas relacionadas com a física como equações diferenciais . Enquanto a notação torna-se incontrolável para os derivados de alta ordem, na prática, são necessários apenas poucas derivados.

Notação de Euler

Euler notação 's utiliza um operador diferencial D, o qual é aplicado a uma função f, para dar o primeiro Df derivado. A segunda derivada é denotada D ² f, e o enésimo derivado é denotado D ⁿ f.

Se y = f (x) é uma variável dependente, em seguida, muitas vezes, o índice x é ligado a D para clarificar a variável independente x. Notação de Euler é então escrito

ou ,

Embora este índice é muitas vezes omitido quando a variável X é compreendido, por exemplo, quando esta é a única variável presente na expressão.

Notação de Euler é útil para informando e resolvendo equações diferenciais lineares.

Calculando o derivado

O derivado de uma função pode, em princípio, ser calculado a partir da definição, considerando o quociente de diferença, e computar o seu limite. Para alguns exemplos, ver Derivativos (exemplos). Na prática, uma vez que os derivados de algumas funções simples são conhecidos, os derivados de outras funções são mais facilmente calculado usando regras para a obtenção de derivados de funções mais complicadas das mais simples.

Derivadas de funções elementares

Além disso, os derivados de algumas funções comuns são úteis para saber.

• Derivados de poderes: se

,

onde r é qualquer número real , então

,

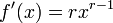sempre que esta função está definida. Por exemplo, se r = 1/2, em seguida

.

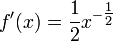e a função é definida apenas para não negativo x. Quando r = 0, esta regra recupera a regra constante.

• Exponenciais e logarítmicas funções:

• Funções trigonométricas :

• Funções trigonométricas inversas:

Regras para encontrar o derivado

Em muitos casos, os cálculos do limite complicadas por aplicação directa do quociente de diferença de Newton pode ser evitado usando regras de diferenciação. Algumas das regras mais básicas são as seguintes.

• Constante regra: se f (x) é constante, então

• Regra da soma:

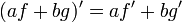para todas as funções f e g e tudo real números a e b.

• Regra do produto:

para todas as funções f e g.

• Regra do quociente:

• Regra da cadeia: Se , Então

.

Exemplo de cálculo

O derivado de

é

Aqui, o segundo termo foi calculado usando a regra da cadeia e terceiros que utilizem a regra do produto: os derivados conhecidos das funções elementares x ², x ^4, sin (x), ln (x) e exp (x) = ^x e também foram utilizados .

Derivados em dimensões superiores

Derivados de funções vector valorizado

A função vectorial y (t) de uma variável real é uma função que envia números reais de vetores em algum espaço vetorial R ^n. A função vectorial pode ser dividido em suas funções coordenar y ₁ (t), y ₂ (t), ..., y _n (t), o que significa que y (t) = (y ₁ (t), ... , y _n (t)). Isto inclui, por exemplo, curvas paramétricas em R ² ou R ^3. As funções de coordenadas são funções a valores reais, de modo que a definição acima de derivado aplica-se a eles. O derivado de y (t) é definido como sendo o vector , denominado vector tangente, cujas coordenadas são as derivadas das funções coordenadas. Isto é,

Equivalentemente,

Se o limite existe. A subtração no numerador é a subtração de vetores, não escalares. Se a derivada de y existe para cada valor de t, então y 'é outra função vector valorizado.

Se e _1, ..., e _n é a base padrão para R ^n, em seguida, y (t) também pode ser escrita como y ₁ (t) e ₁ + ... + y _n (t) e _n. Se assumirmos que a derivada de uma função vectorial mantém o propriedade linearidade, em seguida, o derivado de y (t) deve ser

porque cada um dos vectores de base é uma constante.

Esta generalização é útil, por exemplo, se y (t) é o vector de posição de uma partícula no tempo t; em seguida, o derivado y '(t) é a velocidade da partícula de vector no tempo t.

Derivadas parciais

Suponha que f é uma função que depende mais de uma variável. Por exemplo,

f pode ser reinterpretado como uma família de funções de uma variável indexada pelas outras variáveis:

Em outras palavras, cada valor de x escolhe uma função, denotado f _x, o que é uma função de um número real. Isto é,

Uma vez que um valor de x é escolhido, digamos, um, então f (x, y) determina uma função que envia _um f y para um ² + ay + y ²:

Nesta expressão, a é uma constante, e não uma variável, de modo que f _a é uma função de uma única variável real. Consequentemente, a definição do derivado para uma função de uma variável aplica-se:

O procedimento acima pode ser realizada por qualquer escolha de uma. Montando os derivados em conjunto uma função dá uma função que descreve a variação de f na direcção y:

Esta é a derivada parcial de f em relação a y. Aqui ∂ é um d arredondada chamado o símbolo parcial derivado. Para distingui-la da letra d, ∂ às vezes é pronunciado "der", "del", ou "parcial" em vez de "dee".

Em geral, o derivado parcial de uma função f (x _1, ..., x _n) na direcção x _i no ponto (a ₁ ..., a _n) é definida como sendo:

No quociente diferença acima, todas as variáveis, exceto x _i são mantidos fixos. Essa escolha de valores fixos determina uma função de uma variável

e, por definição,

Em outras palavras, as diferentes opções de um índice de uma família de funções de uma variável apenas como no exemplo acima. Esta expressão também mostra que o cálculo das derivadas parciais reduz para o cálculo dos derivados de uma variável.

Um exemplo importante de uma função de várias variáveis é o caso de um valor escalar função f (x _1, ... x _n) em um domínio no espaço euclidiano R ⁿ (por exemplo, em R ² ou R ³). Neste caso, f tem um derivado parcial ∂ f / ∂ _xj com respeito a cada variável x _j. No ponto A, estes derivados parciais definir o vector

Este vector é denominado gradiente de f em um. Se f é diferenciável em todos os pontos em algum domínio, em seguida, o gradiente é uma função com valor de vetor ∇ f o que leva a um ponto ao vetor ∇ f (a). Por conseguinte, o gradiente determina um campo vetorial.

Derivadas direcionais

Se f for uma função de valor real em R ^n, em seguida, as derivadas parciais de medida f sua variação na direcção dos eixos de coordenadas. Por exemplo, se f é uma função de x e y, em seguida, os seus derivados parciais medir a variação na f na direcção X e a direcção y. Eles não são, no entanto, medir directamente a variação de f em qualquer outra direcção, tal como ao longo das diagonais linha y = x. Estes são medidos utilizando derivados direcionais. Escolha um vector

O derivado de f direccional na direcção de V no ponto x é o limite

Deixe λ ser um escalar. A substituição de h / h para λ muda diferença quociente a λ v de direção em momentos λ diferença quociente de direção do v. Por conseguinte, o derivado direccional na direcção λ v é λ vezes o derivado direccional na direcção v. Devido a isto, derivadas direccionais são muitas vezes considerados apenas para vectores unitários v.

Se existir todas as derivadas parciais de f e são contínuas em x, em seguida, eles determinam o derivado de f direccional na direcção v por fórmula:

Esta é uma consequência da definição do derivada total. Daqui resulta que a derivada direcional é linear em v.

A mesma definição também funciona quando f é uma função com valores em R ^m. Nós só usar a definição acima em cada componente dos vetores. Neste caso, o derivado é um vector direccional em ^Rm.

O derivado total, o diferencial total e o Jacobiana

Seja f uma função de um domínio em R a R. O derivado de f em um ponto um no seu domínio é a melhor aproximação linear para f nesse ponto. Tal como referido acima, este é um número. Geometricamente, se v é um vector a partir de uma unidade, então f '(a), a melhor aproximação linear para f em um, deve ser o comprimento do vector encontrado movendo v para o espaço alvo usando f. (Este vector é denominado pushforward de v por f e é geralmente escrito .) Em outras palavras, se v é medido em termos de distâncias no alvo, então, porque v só pode ser medido através de f, v não parece ser um vetor de unidade porque f não preserva vetores unitários. Em vez v parece ter comprimento f '(a). Se m é maior do que um, então pela escrita f usando funções de coordenadas, o comprimento de V em cada uma das direcções de coordenadas pode ser medido separadamente.

Suponha-se agora que f é uma função de um domínio de ^Rn e R ^m que um é um ponto no domínio de f. A derivada de f em um ainda deve ser a melhor aproximação linear de f em um. Em outras palavras, se v é um vector em R ^n, em seguida, f '(a) deve ser a transformação linear que melhor se aproxima de f. A transformação linear deve conter todas as informações sobre como f transforma vetores em um de vetores em f (a), e em símbolos, o que significa que deve ser a transformação linear f '(a) de tal forma que

Aqui h é um vector no R ^n, de modo a norma no denominador é o comprimento padrão em R ^n. No entanto, f '(a), h é um vector em R ^m, e a norma no numerador é o comprimento padrão em ^Rm. A transformação linear f (a), se existir, é chamada a derivada total de f em a ou a (Total) diferencial de f a uma.

Se a derivada total existe em um, então existem todas as derivadas parciais de f a uma. Se escrever f usando funções de coordenadas, de modo que f = (f _1, f _2, ..., f _m), em seguida, o derivado total pode ser expressa como uma matriz chamada Matriz Jacobiana de f em um:

A existência do Jacobiana é estritamente mais forte do que a existência de todas as derivadas parciais, mas se existir as derivadas parciais e satisfazer condições suaves suavidade, então existe a derivada total e é dada pela Jacobiana.

A definição da derivada total engloba a definição do derivado em uma variável. Neste caso, existe a derivada total se e somente se o derivado habitual existir. A matriz Jacobiana reduz-se a uma matriz 1 × 1 cuja única entrada é o derivado de f (x). Esta matriz 1 × 1 satisfaz a propriedade de que f (a + h) - f (a) - f '(a) H é aproximadamente zero, por outras palavras, que

Até variáveis mudam, esta é a afirmação de que a função é a melhor aproximação linear de f em um.

O derivado total de uma função não dá uma outra função da mesma maneira que caso de uma variável. Isto é porque a derivada total de uma função multivariável tem de registar muito mais informação do que a derivada de uma única variável de função. Em vez disso, a derivada total dá uma função da pacote tangente da origem para o pacote tangente do alvo.

Generalizações

O conceito de um derivado pode ser estendida a muitos outros ajustes. O traço comum é que a derivada de uma função num ponto serve como um aproximação linear da função nesse ponto.

• Uma generalização importante das preocupações derivados complexos funções de variáveis, tais como complexos de funções (um domínio em) a números complexos C para C. A noção de o derivado de uma tal função é obtido através da substituição de variáveis reais com variáveis complexas na definição. No entanto, esta definição inocente esconde algumas propriedades muito profundas. Se C é identificada com R² escrevendo um número complexo como z x + y i, em seguida, uma função diferenciável de C para C é certamente diferenciável como uma função de R a R ² ² (no sentido em que existem todos os seus derivados parciais) , mas o inverso não é verdadeiro em geral: o derivado complexo só existe se o derivado real é linear complexa e isso impõe relações entre as derivadas parciais chamado Equações Cauchy Riemann - veja funções holomorfas.

• Outra generalização diz respeito a funções entre variedades diferenciáveis ou lisas. Intuitivamente falando uma M tal colector é um espaço que pode ser aproximada perto de cada ponto x de um espaço vetor chamado sua espaço tangente: o exemplo prototípico é um superfície lisa em R ³. O derivado (ou diferencial) de um (diferenciável) f: M → N entre condutas, em um ponto x em M, então é uma mapa linear a partir do espaço de tangente M em x para o espaço tangente de N em f (x). A função derivada torna-se um mapa entre a feixes tangentes de M e N. Esta definição é fundamental em geometria diferencial e tem muitos usos - veja pushforward (diferencial) e pullback (geometria diferencial).

• A diferenciação pode também ser definida para mapas entre dimensão infinita espaços vetoriais , tais como Espaços de Banach e Espaços de Fréchet. Há uma generalização tanto do derivado direccional, o chamado Gâteaux derivado, e do diferencial, o chamado Derivado Fréchet.

• Uma deficiência do derivado clássica é que nem muito muitas funções são diferenciáveis. No entanto, há uma maneira de estender a noção do derivado para que todos funções contínuas e muitas outras funções podem ser diferenciadas usando um conceito conhecido como o derivado fraco. A idéia é incorporar as funções contínuas em um espaço maior, chamado o espaço de distribuições e requerem apenas que uma função é diferenciável "em média".

• As propriedades do derivado ter inspirado a introdução e estudo de diversos objectos semelhantes em álgebra e topologia - ver, por exemplo, álgebra diferencial.