
Proporção áurea
Informações de fundo
Crianças SOS têm produzido uma seleção de artigos da Wikipedia para escolas desde 2005. Criança patrocínio ajuda as crianças uma a uma http://www.sponsor-a-child.org.uk/ .

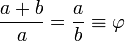 .
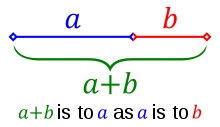
. Em matemática e as artes , duas quantidades estão na proporção áurea se o razão entre a soma das quantidades para a quantidade maior é igual à razão entre a quantidade maior para o mais pequeno. A figura da direita mostra a relação geométrica. Expressa algebricamente:
onde a letra grega phi ( 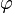 ) Representa a proporção áurea. Seu valor é:
) Representa a proporção áurea. Seu valor é:
A proporção áurea é também chamada de seção áurea (latim: aurea sectio) ou média de ouro. Outros nomes incluem extrema e média proporção, seção medial, proporção divina, seção divina (do latim: sectio divina), proporção áurea, corte dourado, número dourado e.
Muitos século 20 artistas e arquitetos proporcionaram seus trabalhos para aproximar a relação-especialmente dourada sob a forma do rectângulo de ouro, em que a razão entre o lado mais longo para o mais curto é o rácio acreditando-dourado que esta proporção seja esteticamente agradável (ver Aplicações e observações abaixo). matemáticos desde Euclides estudaram as propriedades de a proporção de ouro, incluindo a sua aparência em as dimensões de um pentágono regular e de uma rectângulo de ouro, que pode ser cortada num quadrado e um pequeno rectângulo com a mesma relação de aspecto. A proporção áurea também tem sido usado para analisar as proporções de objetos naturais, bem como sistemas feitos pelo homem, tais como mercados financeiros, em alguns casos baseados em acessos aos dados duvidosos.
Cálculo
| |
| Binário | 1,1001111000110111011 ... |
| Decimal | 1,6180339887498948482 ... |
| Hexadecimal | 1.9E3779B97F4A7C15F39 ... |
| Fracção contínua | 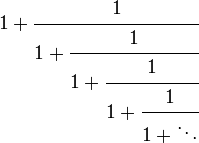 |
| Forma algébrica |  |
| Infinita série | 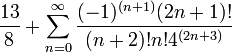 |
Duas quantidades a e b são ditos ser na razão de ouro φ se:
Um método para encontrar o valor de φ é começar com a fracção esquerda. Através de simplificar a fração e substituindo em b / a = 1 / φ,
mostra-se que
Multiplicando por φ dá
que pode ser rearranjada para
Usando a fórmula quadrática , são obtidas duas soluções:
e
Devido ao facto de φ é a relação entre comprimento e largura de um rectângulo, que são não-zero, a solução positiva deve ser escolhida:
História


A proporção áurea tem fascinado os intelectuais ocidentais de interesses diversos para pelo menos 2.400 anos. Conforme Mario Livio:
Algumas das maiores mentes matemáticas de todas as idades, desde Pitágoras e Euclides na Grécia antiga , medieval através do matemático italiano Leonardo de Pisa eo astrônomo renascentista Johannes Kepler , às actuais personalidades científicas, tais como Oxford físico Roger Penrose, passaram horas intermináveis sobre esta relação simples e suas propriedades. Mas o fascínio com a Razão Áurea não se limita apenas aos matemáticos. Biólogos, artistas, músicos, historiadores, arquitetos, psicólogos e até místicos têm ponderado e debatido a base de sua onipresença e de recurso. Na verdade, é provavelmente justo dizer que a Razão Áurea tem inspirado pensadores de todas as disciplinas como nenhum outro número na história da matemática.
Gregos antigos matemáticos primeiro estudou o que hoje chamamos a relação dourada devido a sua aparência freqüente em geometria . A divisão de uma linha em "razão extrema e média" (seção dourada) é importante na geometria do normal pentagramas e pentágonos. A descoberta gregos geralmente atribuída deste conceito de Pitágoras ou o seu seguidores. O pentagrama regular, que tem um pentágono regular inscrito dentro dele, era símbolo os pitagóricos '.
Euclides 's Elements ( grego : Στοιχεῖα) fornece a definição escrita primeiramente conhecida de que é agora chamado a proporção áurea: "Uma linha reta é dito ter sido cortado em razão extrema e média quando, como toda a linha é o maior segmento , assim é o maior para o menor. " Euclides explica uma construção para o corte (corte) de uma linha "em razão extrema e média", ou seja, a proporção áurea. Durante todo o Elements, várias proposições ( teoremas na terminologia moderna) e suas provas empregar a proporção áurea. Algumas dessas proposições mostram que a proporção áurea é um número irracional .
O nome "razão extrema e média" foi o principal termo utilizado a partir do terceiro século aC até o século 18.
A história moderna da relação dourada começa com Luca Pacioli de De Divina Proportione de 1509, que capturou a imaginação de artistas, arquitectos, cientistas e místicos com as propriedades, matemática e outra, da proporção áurea.
A primeira aproximação conhecida do (inverso) razão de ouro por uma fração decimal , afirmou que "cerca de 0,6180340", foi escrito em 1597 por Michael do Maestlin Universidade de Tübingen em uma carta a seu ex-aluno Johannes Kepler .
Desde o século 20 , a proporção áurea foi representado pela letra grega Φ ou φ ( phi, depois Phidias, um escultor que se diz ter empregado-lo) ou menos comumente por τ ( tau, a primeira letra do grego antigo raiz corte τομή-intencionado).
Timeline
Timeline de acordo com Priya Hemenway:
- Phidias (490-430 aC) fazem as Parthenon estátuas que parecem encarnar a proporção áurea.
- Platão (427-347 aC), em seu Timeu, descreve cinco possíveis sólidos regulares (os sólidos platônicos : o tetraedro , cubo , octaedro , dodecaedro, e icosaedro), algumas das quais estão relacionadas com a razão de ouro.
- Euclid (.. 265 c 325-c BC), em seus elementos , deu a primeira definição gravada da proporção áurea, que ele chamou, como traduzida em Inglês, "razão extrema e média" (em grego: ἄκρος καὶ μέσος λόγος).
- Fibonacci (1170-1250) mencionou a série numérica agora nomeado após ele em sua Liber Abaci; a proporção de elementos sequenciais de a sequência de Fibonacci se aproxima assimptoticamente a proporção de ouro.
- Luca Pacioli (1445-1517) define a proporção de ouro como a "proporção divina" em sua Divina Proportione.
- Michael Maestlin (1550-1631) publica a primeira aproximação conhecida do (inverso) razão de ouro como uma fração decimal .
- Johannes Kepler (1571-1630) prova que a proporção áurea é o limite da relação de números de Fibonacci consecutivos, e descreve a relação dourada como uma "jóia preciosa": "Geometria tem dois grandes tesouros: uma é o Teorema de Pitágoras , e por outro, a divisão de uma linha em relação extremo e dizer: a primeira, podemos comparar a uma medida de ouro, o segundo, podemos citar uma jóia preciosa ". Estes dois são combinados no património da Kepler triângulo.
- Charles Bonnet (1720-1793) assinala que na espiral phyllotaxis de plantas indo no sentido horário e anti-horário eram freqüentemente dois sucessiva série de Fibonacci.
- Martin Ohm (1792-1872) é acreditado para ser o primeiro a usar o termo goldener Schnitt (seção dourada) para descrever essa relação, em 1835.
- Édouard Lucas (1842-1891) dá a seqüência numérica agora conhecida como a seqüência de Fibonacci seu nome atual.
- Mark Barr (século 20) sugere a letra grega phi (φ), a letra inicial do nome do escultor grego Fídias, como um símbolo para a relação dourada.
- Roger Penrose (b.1931) descobriu um padrão simétrico que usa a proporção áurea no domínio da tilings aperiódicos, o que levou a novas descobertas sobre quasicristais.
Aplicações e observações
Estética
De Divina Proportione, uma obra em três volumes por Luca Pacioli, foi publicado em 1509. Pacioli, um Franciscano frade, foi conhecido principalmente como um matemático, mas ele também foi treinado e muito interessado em arte. De Divina Proportione explorou a matemática da proporção áurea. Embora muitas vezes é dito que Pacioli defendeu o pedido da proporção áurea para produzir, proporções harmoniosas agradáveis, Livio salienta que a interpretação tem sido atribuída a um erro em 1799, e que na verdade Pacioli defendeu a Vitruviano sistema de proporções racionais. Pacioli também viu significado religioso católico na relação, o que levou o título de seu trabalho. Contendo ilustrações dos sólidos regulares por Leonardo da Vinci , amigo de longa data de Pacioli e colaborador, De Divina Proportione foi uma grande influência sobre gerações de artistas e arquitetos.
Arquitetura

A fachada do Parthenon, bem como elementos de sua fachada e em outros lugares são dito por alguns de ser circunscrito por retângulos dourados. Outros estudiosos negam que os gregos tinham qualquer associação estética com relação dourada. Por exemplo, Midhat J. Gazale diz: "Não foi até Euclides, no entanto, que foram estudadas propriedades matemáticas da relação dourada. No Elements (308 aC), o matemático grego meramente considerado o número como um número irracional interessante, em conexão com os rácios médios e extremos. Sua ocorrência em pentágonos regulares e decágonos foi devidamente respeitado, bem como no dodecaedro (a poliedro regular cujos rostos são doze pentágonos regulares). Na verdade, é exemplar que a grande Euclid, contrariamente ao que gerações de místicos que se seguiram, seria sobriamente tratar esse número para o que é, sem anexar a ele que não seja as suas propriedades factuais. "E Keith Devlin diz: "Certamente, a afirmação frequentemente repetida de que o Parthenon, em Atenas é baseada na proporção áurea não é suportado por medidas reais. Na verdade, toda a história sobre os gregos e proporção áurea parece ser sem fundamento. A única coisa que sabemos com certeza é que Euclides, em seu famoso livro Elements, escrito por volta de 300 aC, mostrou como calcular seu valor. " Fontes quase-contemporâneos como Vitruvius discutir exclusivamente proporções que podem ser expressos em números inteiros, ou seja, proporcional ao contrário de proporções irracionais.
A análise geométrica de 2004, de uma pesquisa mais adiantada no Grande Mesquita de Kairouan revela uma aplicação coerente da proporção áurea em todo o projeto, de acordo com Boussora e Mazouz. Eles encontraram razões para fechar a proporção de ouro na proporção global do plano e no dimensionamento do espaço de oração, o tribunal, ea minarete. Os autores notaram, no entanto, que as zonas onde a proporção próxima da razão de ouro foram encontradas não são parte da construção original, e teorizam que estes elementos foram adicionados em uma reconstrução.
O suíço arquiteto Le Corbusier, famosa por suas contribuições para o moderno estilo internacional, centrou sua filosofia de design em sistemas de harmonia e proporção. A fé de Le Corbusier na ordem matemática do universo estava intimamente ligada à proporção áurea e da série de Fibonacci, que ele descreveu como "ritmos aparentes aos olhos e claras nas suas relações com o outro. E esses ritmos são a própria raiz de atividades humanas. Elas ressoam no homem por uma inevitabilidade biológica, a mesma inevitabilidade fina que faz com que o traçado para fora da Seção de Ouro por crianças, velhos, selvagens e os eruditos ".
Le Corbusier explicitamente utilizada a proporção de ouro em sua Sistema para o modulor escala de proporção arquitetônica. Ele viu este sistema como uma continuação da longa tradição de Vitruvius, Leonardo da Vinci " Homem Vitruviano ", o trabalho de Alberti, e outras pessoas que utilizaram as proporções do corpo humano para melhorar a aparência e função da arquitectura . Para além da razão de ouro, Corbusier baseado o sistema de medições humanos, números de Fibonacci , e da unidade de casal. Ele levou a sugestão de a proporção áurea em proporções humanas a um extremo: ele seccionado altura de seu corpo humano modelo no umbigo com as duas seções em razão de ouro, então subdividida essas seções em razão de ouro na altura dos joelhos e da garganta; ele usou essas proporções proporção áurea no Sistema Modulor. De Le Corbusier 1927 Villa Stein em Garches exemplificado aplicação do sistema Modulor. O plano do villa rectangular, elevação e estrutura interna retângulos de ouro de perto aproximados.
Outro arquiteto suíço, Mario Botta, baseia muitos de seus desenhos sobre figuras geométricas. Várias casas privadas que projetou na Suíça são compostas de quadrados e círculos, cubos e cilindros. Em uma casa que ele projetou em Origlio, a proporção áurea é a proporção entre a secção central e as secções laterais da casa.
Em um livro recente, o autor Jason Elliot especularam que a proporção áurea foi utilizado pelos designers do Naqsh-e Jahan Square e da mesquita adjacente Lotfollah.
Pintura
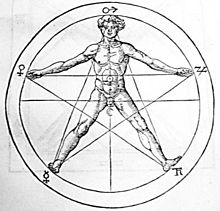
O filósofo do século 16 Heinrich Agripa desenhou um homem sobre um pentagrama dentro de um círculo, o que implica uma relação com a proporção áurea.
Leonardo da Vinci ilustrações 's de poliedros em De Proportione divina (sobre a proporção divina) e seus pontos de vista que algumas proporções corporais apresentam a proporção áurea levaram alguns estudiosos a especular que ele incorporou a proporção de ouro em suas pinturas. Mas a sugestão de que sua Mona Lisa , por exemplo, emprega proporções proporção áurea, não é apoiada por qualquer coisa nos próprios escritos de Leonardo. Da mesma forma, embora a Homem Vitruviano é freqüentemente mostrado em conexão com a proporção áurea, as proporções da figura realmente não combiná-lo, eo texto apenas menciona rácios de números inteiros.
Salvador Dalí, influenciado pelas obras de Matila Ghyka, explicitamente utilizada a proporção de ouro em sua obra-prima, O Sacramento da Última Ceia. As dimensões da tela são um rectângulo dourado. Uma enorme dodecaedro, em perspectiva, de modo que as arestas aparecem na razão de ouro para o outro, é suspensa de cima e por trás de Jesus e domina a composição.
Mondrian foi dito ter usado a seção áurea extensivamente em suas pinturas geométricas, embora outros especialistas (incluindo crítico Yve-Alain Bois) têm contestado esta afirmação.
Um estudo estatístico em 565 obras de arte de diferentes grandes pintores, realizado em 1999, constatou que esses artistas não tinha usado a proporção áurea no tamanho de suas telas. O estudo concluiu que a proporção média dos dois lados das pinturas estudadas é 1,34, com médias para artistas individuais que variam de 1,04 (Goya) para 1,46 (Bellini). Por outro lado, Pablo Tosto listados mais de 350 obras de artistas bem conhecidos, incluindo mais de 100 que têm telas com retângulo de ouro e raiz-5 proporções, e outros com proporções como root-2, 3, 4 e 6.
Design de livros
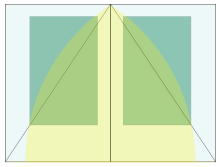
Conforme Jan Tschichold,
Houve um tempo em que os desvios relativamente aos página verdadeiramente belas proporções 2: 3, 1: √3, ea Seção de Ouro eram raros. Muitos livros produzidos entre 1550 e 1770 mostram essas proporções exatamente, para dentro de meio milímetro.
Desenho industrial
Algumas fontes afirmam que a proporção áurea é comumente usado no projeto todos os dias, por exemplo, nos formatos de cartões postais, cartas de baralho, pôsteres, televisores de tela ampla, fotografias e placas do interruptor de luz.
Música
Analisa Ernő Lendvai As obras de Béla Bartók como sendo baseado em dois sistemas opostos, o da relação dourada e as escala acústica, embora outros estudiosos de música rejeitar esta análise. Em Bartok de Música para Cordas, Percussão e Celesta a progressão xilofone ocorre nos intervalos de 1: 2: 3: 5: 8: 5: 3: 2: 1. Compositor francês Erik Satie utilizou a proporção áurea em várias de suas peças, incluindo Sonneries de la Rose + Croix. A proporção áurea é também evidente na organização das seções na música de Debussy Reflets dans l'eau (Reflexos na água), a partir de imagens (primeira série de 1905), em que "a sequência de teclas é balizado pelos intervalos de 34, 21, 13 e 8, eo clímax principal senta-se na posição de phi . "
O musicólogo Roy Howat observou que os limites formais de La Mer correspondem exactamente à seção áurea. Trezise encontra a evidência intrínseca "notável", mas adverte que nenhuma evidência escrita ou relatada sugere que Debussy buscou conscientemente tais proporções.
Pearl Drums posiciona as saídas de ar em seus modelos premium de mestrado com base na proporção áurea. A empresa alega que este arranjo melhora a resposta de graves e solicitou uma patentear nesta inovação.
Embora Heinz Bohlen propôs a não-oitava-repetição Escala 833 centavos com base em tons de combinação, os recursos de ajuste de relações baseadas na razão de ouro. Como um intervalo musical a proporção 1.618 ... é ... 833,090 centavos (Play).
Natureza

Adolf Zeising, cujo principal interesse era a matemática ea filosofia, encontrou a proporção áurea expressa no arranjo dos ramos ao longo das hastes das plantas e das veias nas folhas. Estendeu a investigação para os esqueletos de animais e as suas ramificações de veias e nervos, para as proporções de compostos químicos e a geometria de cristais, mesmo com a utilização de proporção em artísticas. Nesses fenômenos que viu a proporção áurea operando como um direito universal. Em conexão com seu esquema para proporções do corpo humano baseados em dourado-ratio, Zeising escreveu, em 1854, de uma lei universal ", no qual está contido o princípio-base de tudo formativa que se esforça para a beleza ea integralidade nos reinos da natureza e da arte, e que permeia, tal como um ideal primordial espiritual, todas as estruturas, formas e proporções, se cósmica ou indivíduo, orgânico ou inorgânico, acústico ou óptico;. o que encontra a sua realização mais ampla, no entanto, sob a forma humana "
Em 2010, a revista Science relatou que a proporção áurea está presente em escala atômica na ressonância magnética de spins em cristais cobalto niobato.
Vários pesquisadores têm proposto conexões entre a proporção de ouro e genoma humano de ADN .
No entanto, alguns têm argumentado que muitas das manifestações aparentes do ouro significa na natureza, especialmente no que diz respeito às dimensões dos animais, são, na verdade fictícia.
Otimização
A proporção áurea é a chave para o Pesquisa seção áurea.
Estudos de percepção
Estudos realizados por psicólogos, começando com Fechner, foram concebidas para testar a idéia de que a proporção áurea desempenha um papel na percepção humana da beleza. Enquanto Fechner encontrada uma preferência por razões retângulo centrado na relação dourada, mais tarde tenta testar cuidadosamente tal hipótese ter sido, na melhor das hipóteses, inconclusivos.
Matemática
Golden Ratio conjugado
A raiz negativa da equação quadrática para φ (a "raiz conjugado") é
O valor absoluto desta quantidade (≈ 0,618) corresponde à relação entre o comprimento feita na ordem inversa (comprimento de segmento mais curto ao longo do comprimento do segmento mais longo, b / a), e é por vezes referida como a proporção de conjugado de ouro. É denotado aqui pela capital Phi (Φ):
Alternativamente, Φ pode ser expressa como
Isto ilustra a propriedade única de a proporção de ouro entre números positivos, que
ou o seu inverso:
Isto significa 0,61803 ...: 1 = 1: 1,61803 ....
Provas curtas de irracionalidade
Contradição de uma expressão em termos mais baixos
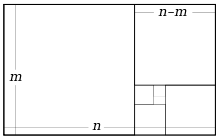
Lembre-se que:
- o todo é a parte mais mais a parte mais curta;
- o todo é a parte mais longa que a parte mais longa é a parte mais curta.
Se chamarmos toda a n e a parte mais longa m, então a segunda afirmação acima torna-se
- n é a m m é como a n - m,
ou, algebricamente
Dizer que é φ meios racionais que φ é uma fracção n / m em que n e m são números inteiros. Podemos tomar n / m para ser menor em termos e n e m que ser positivo. Mas se n / m é menor em termos, então a identidade marcado (*) acima diz m / (n - m) é em termos ainda mais baixos. Isso é uma contradição que se segue a partir da suposição de que φ é racional.
Derivação de irracionalidade de √5
Outra prova de curto talvez mais comumente conhecido da irracionalidade da proporção áurea faz uso do fechamento dos números racionais sob adição e multiplicação. Se 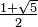 é racional, em seguida,
é racional, em seguida,  também é racional, que é uma contradição se ele já é conhecido que a raiz quadrada de um não- praça número natural é irracional.
também é racional, que é uma contradição se ele já é conhecido que a raiz quadrada de um não- praça número natural é irracional.
Formas alternativas
A fórmula φ = 1 + 1 / φ pode ser expandido de forma recursiva para obter um fração continuou durante a relação dourada:
e seu recíproco:
O convergentes dessas frações contínuas (1/1, 2/1, 3/2, 5/3, 8/5, 13/8, ..., ou 1/1, 1/2, 2/3, 3/5 , 5/8, 8/13, ...) são proporções de sucessivos números de Fibonacci .
A equação φ 2 = 1 + φ igualmente produz a contínua raiz quadrada , ou infinito surd, forma:
Uma série infinita pode ser derivada de expressar phi:
Além disso:
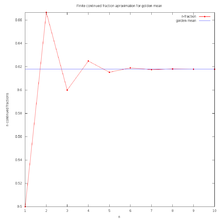
Estes correspondem ao facto de que o comprimento da diagonal de um pentágono regular é φ vezes o comprimento do seu lado, e as relações semelhantes em uma pentagrama.
Geometria
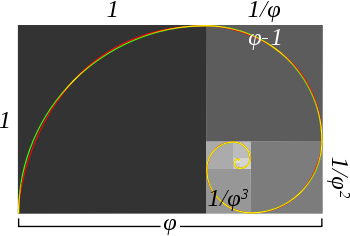
O φ número transforma-se frequentemente em geometria , particularmente em figuras com pentagonal simetria . O comprimento de um regular pentágono de diagonal é φ vezes seu lado. Os vértices de um regular icosaedro são aqueles de três mutuamente ortogonal retângulos dourados.
Não é conhecido nenhum geral algoritmo para providenciar um determinado número de nós uniformemente sobre uma esfera, por qualquer uma das várias definições de uma distribuição uniforme (ver, por exemplo, Problema Thomson). No entanto, uma aproximação útil resultar da divisão da esfera em faixas paralelas de igual área e colocando um nó em cada banda em longitudes espaçadas por uma seção áurea do círculo, ou seja, 360 ° / φ ≅ 222,5 °. Este método foi utilizado para organizar os 1.500 espelhos do estudante-participativa satélite Starshine-3.
Dividir um segmento de linha
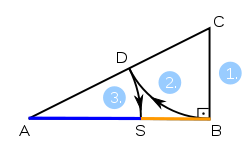
O seguinte algoritmo produz uma construção geométrica que divide um segmento de linha em dois segmentos de linha, onde a razão entre o tempo para o segmento de linha mais curta é a proporção de ouro:
- Tendo um segmento de recta AB, BC construir uma perpendicular no ponto B, com BC metade do comprimento de AB. Desenhe o hipotenusa AC.
- Desenhe um círculo com centro C e raio BC. Este círculo cruza a hipotenusa AC no ponto D.
- Desenhe um círculo com centro A e raio AD. Este círculo intersecta o segmento de linha original AB no ponto S. Ponto S divide o segmento AB original em segmentos de linha AS e SB com comprimentos na proporção áurea.
Triângulo dourado, pentágono e pentagrama
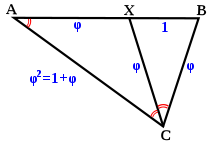
Triângulo dourado
O triângulo dourado pode ser caracterizado como um triângulo isósceles ABC com a propriedade que bissetriz do ângulo C produz um novo triângulo CXB que é um triângulo semelhante à original.
Se o ângulo de BCX = α, em seguida, XCA = α por causa da bissecção, e CAB = α por causa dos triângulos semelhantes; ABC = 2α da simetria isósceles original, e BXC = 2α por semelhança. Os ângulos de um triângulo somam 180 °, de modo 5α = 180, dando α = 36 °. Então, os ângulos do triângulo dourado são, portanto, 36 ° -72 ° -72 °. Os ângulos do triângulo isósceles obtuso restante AXC (às vezes chamado de gnomon dourado) são 36 ° -36 ° -108 °.
Suponha XB tem comprimento 1, e chamamos comprimento BC φ. Por causa da triângulos isósceles XC = XA e BC = XC, assim que estes também são comprimento φ. Comprimento AC = AB, portanto, é igual a φ + 1. Mas triângulo ABC é semelhante ao triângulo CXB, então AC / BC = BC / BX, e assim por AC também é igual a 2 φ. Assim φ 2 = φ + 1, confirmando que φ é de fato a relação dourada.
Da mesma forma, a razão entre a área do maior AXC triângulo à CXB menor é igual a φ, enquanto o razão inversa é φ - 1.
Pentágono
Em um pentágono regular a relação entre um lado e uma diagonal é 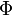 (Ou seja, 1 / φ), enquanto que intersectam as diagonais secção mutuamente na proporção de ouro.
(Ou seja, 1 / φ), enquanto que intersectam as diagonais secção mutuamente na proporção de ouro.
Construção de Odom
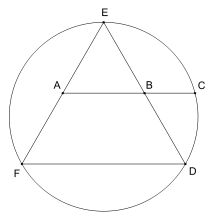
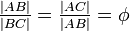
George Odom deu uma construção extremamente simples para φ envolvendo um triângulo equilátero: se um triângulo equilátero inscrito em um círculo eo segmento de linha que une os pontos médios de dois lados é produzido para cruzar o círculo em um dos dois pontos, então estes três pontos estão em proporção áurea. Esse resultado é uma conseqüência direta da intersectando acordes teorema e pode ser utilizado para construir um pentágono regular, uma construção que atraíram a atenção do geômetra canadense observou HSM Coxeter que o publicou em nome de Odom como um diagrama no American Mathematical Monthly acompanhada pela única palavra: "Eis!"
Pentagrama
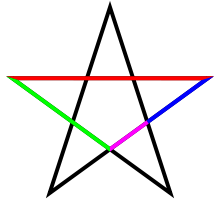
A razão de ouro desempenha um papel importante na geometria de pentagramas. Cada interseção de seções bordas outras arestas na proporção áurea. Além disso, a razão entre o comprimento do segmento mais curto para o segmento delimitada pelas duas bordas que se intersectam (um lado do pentágono no centro do pentagrama) é φ, como as quatro cores mostra a ilustração.
O pentagrama inclui dez triângulos isósceles : cinco aguda e cinco obtusos triângulos isósceles. Em todos eles, a razão entre o lado mais comprido para o lado curto é φ. Os triângulos são agudos triângulos dourados. Os triângulos isósceles são obtusos gnômons douradas.
Teorema de Ptolomeu

As propriedades proporção áurea de um pentágono regular pode ser confirmada através da aplicação O teorema de ptolemy para o quadrilátero formado por remoção de um dos seus vértices. Se borda longa e diagonais do quadrilátero são B e extremidades curtas são um, então o teorema de Ptolomeu dá b 2 = um 2 + ab que os rendimentos
Scalenity de triângulos
Considere-se um triângulo com lados de comprimentos a, b, e c, por ordem decrescente. Definir o "scalenity" do triângulo para ser o menor dos dois rácios de a / b e b / c. O scalenity é sempre menor que φ e pode ser feita tão próxima quanto desejado para φ.
Os lados do triângulo cujos formar uma progressão geométrica
Se os comprimentos dos lados de um triângulo forma um progressão geométrica e estão na razão 1: r: r 2, onde r é a razão comum, então R deve situar-se na gama φ-1 <r <φ, que é uma consequência do desigualdade triangular (a soma de quaisquer dois lados de um triângulo deve ser estritamente maior que o comprimento do terceiro lado). Se r = φ, em seguida, os dois lados são mais curtos e 1 φ mas sua soma é φ 2, assim r <φ. Um cálculo semelhante mostra que r> φ-1. Um triângulo cujos lados estão na razão 1: √φ: φ é um triângulo rectângulo (porque 1 + φ = φ 2) conhecido como um Kepler triângulo.
Golden Triangle, losango, e rhombic triacontahedron
A losango de ouro é um losango cujas diagonais estão na proporção áurea. O triacontahedron rômbico é um politopo convexo que tem uma propriedade muito especial: todas as suas faces são losangos de ouro. No rhombic triacontahedron o ângulo diedro entre quaisquer dois losangos adjacentes é 144 °, o qual é duas vezes o ângulo de um isósceles triângulo de ouro e quatro vezes o seu ângulo mais agudo.
Relação com a seqüência de Fibonacci
A matemática da proporção áurea e da seqüência de Fibonacci estão intimamente interligados. A seqüência de Fibonacci é:
- 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, ....
O de forma fechada expressão (conhecido como Fórmula de Binet, embora já era conhecido pela Abraham de Moivre) para a sequência de Fibonacci envolve a proporção áurea:
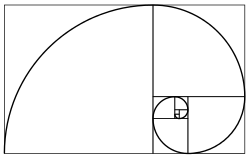
A proporção áurea é o limite das razões de termos sucessivos da seqüência de Fibonacci (ou qualquer seqüência de Fibonacci-like), como mostrado originalmente pela Kepler :
Portanto, se um número de Fibonacci é dividido pelo seu antecessor imediato na sequência, o quociente aproxima φ; por exemplo, 987/610 ≈ 1,6180327868852. Estas aproximações são alternadamente inferior e superior em φ, e convergem em φ como o aumento de números de Fibonacci, e:
De modo mais geral:
onde acima, as proporções de termos consecutivos da sequência de Fibonacci, é um caso quando  .
.
Além disso, as potências sucessivas de φ obedecer à Fibonacci recorrência:
Esta identidade permite que qualquer polinómio em φ para ser reduzido para uma expressão linear. Por exemplo:
No entanto, esta não é uma propriedade especial de φ, porque polinómios em x para qualquer solução de uma equação quadrática pode ser reduzido de uma maneira análoga, mediante a aplicação de:
para determinados coeficientes a, b de tal forma que x satisfaz a equação. Mesmo mais genericamente, qualquer função racional (com coeficientes racionais) da raiz de uma irredutívelnº graus polinômio sobre os números racionais pode ser reduzido a um polinômio de graun- 1. Dito em termos deteoria de campo, se α é raiz de uma irredutívelnth polinomial graus de, em seguida,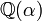 tem um graunatravés
tem um graunatravés , com base
, com base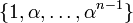 .
.
Simetrias
A proporção áurea e proporção áurea inversa  tem um conjunto de simetrias que preservam e interrelacionam-los. Ambos são conservados pelas transformações lineares fracionários
tem um conjunto de simetrias que preservam e interrelacionam-los. Ambos são conservados pelas transformações lineares fracionários 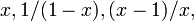 - este facto corresponde à identidade e a equação quadrática definição. Além disso, eles são trocados pelos três mapas
- este facto corresponde à identidade e a equação quadrática definição. Além disso, eles são trocados pelos três mapas 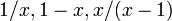 - eles são recíprocos, simétrica em torno
- eles são recíprocos, simétrica em torno 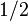 , e (projetivamente) simétrica cerca de 2.
, e (projetivamente) simétrica cerca de 2.
Mais profundamente, estes mapas formam um subgrupo dogrupo modular isomorfo aogrupo simétrico em três letras,
isomorfo aogrupo simétrico em três letras,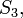 correspondente aoestabilizador do conjunto
correspondente aoestabilizador do conjunto de três pontos padrão nalinha projectiva, e as simetrias correspondem ao quociente
de três pontos padrão nalinha projectiva, e as simetrias correspondem ao quociente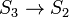 - o subgrupo
- o subgrupo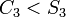 que consiste os três ciclos e a identidade
que consiste os três ciclos e a identidade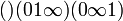 define os dois números, enquanto que os dois ciclos de trocar estes, realizando assim o mapa.
define os dois números, enquanto que os dois ciclos de trocar estes, realizando assim o mapa.
Outras propriedades
A proporção áurea tem a expressão mais simples (e convergência mais lenta) como uma expansão em frações continuado de qualquer número irracional (veja Formas alternativas acima). É, por essa razão, um dos piores casos de aproximação teorema de Lagrange e é um caso extremal da desigualdade Hurwitz para aproximações diofantinas. Isto pode ser porque ângulos perto da proporção áurea muitas vezes mostram-se em phyllotaxis (o crescimento de plantas).
O polinômio quadrático definição ea relação conjugado levam a valores decimais que têm a sua parte fracionária em comum com φ:
A seqüência de poderes de φ contém estes valores ... 0,618, 1,0, 1,618 ..., 2.618 ...; mais geralmente, qualquer poder de φ é igual à soma das duas potências imediatamente anteriores:
Como resultado, pode-se facilmente decompor qualquer poder de φ em um múltiplo de φ e uma constante. O múltiplo ea constante são sempre os números de Fibonacci adjacentes. Isto leva a uma outra propriedade dos poderes positivos de φ:
Se  , Então:
, Então:
Quando a proporção de ouro é usado como base de umsistema numérico(verbase de proporção de Ouro, por vezes apelidadophinaryouφ-pulmonar), cada inteiro tem uma representação de terminação, apesar φ sendo irracional, mas cada fracção tem uma representação de não-encerramento.
A proporção áurea é uma unidade fundamental do campo de número algébrico  e é um número Pisot-Vijayaraghavan. No campo
e é um número Pisot-Vijayaraghavan. No campo  , temos
, temos 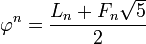 , Onde
, Onde 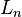 é o
é o  -th número Lucas.
-th número Lucas.
A razão de ouro, também aparece nageometria hiperbólica, como a distância máxima a partir de um ponto de um lado de umtriângulo ideal para o mais perto dos outros dois lados: esta distância, o comprimento do lado dotriângulo equilátero formado pelos pontos de tangente de um círculo inscrito dentro do triângulo ideal, é de 4 ln φ.
Expansão decimal
Expansão decimal da proporção áurea pode ser calculado diretamente a partir da expressão
com √5 ≈ 2,2360679774997896964. O raiz quadrada de 5 pode ser calculada com ométodo da Babilônia, começando com uma estimativa inicial, comoxφ = 2 eiteração
paran= 1, 2, 3, ..., até que a diferença entrexnex n-1se torna zero, para o número desejado de dígitos.
O algoritmo para babilônico √5 é equivalente ao método de Newton para resolver a equação x 2 - 5 = 0. Na sua forma mais geral, o método de Newton pode ser aplicado directamente a qualquer equação algébrica, incluindo a equação x 2 - x - 1 = 0 que define a proporção áurea. Isto dá uma iteração que converge para a razão de ouro em si,
para uma estimativa inicial adequadaxφ tais comox= φ 1. Um método ligeiramente mais rápido é reescrever a equação comox- 1 - 1 /x= 0, caso em que se torna a iteração Newton
Estas iterações todos convergem de forma quadrática; isto é, cada passo aproximadamente duplica o número de dígitos correctas. A proporção áurea é, portanto, relativamente fácil de calcular com precisão arbitrária. O tempo necessário para calcular n dígitos de a proporção de ouro é proporcional ao tempo necessário para dividir dois n números de quatro dígitos. Isto é consideravelmente mais rápido do que algoritmos conhecidos para os números transcendentais π e e .
Uma alternativa facilmente programado usando apenas aritmética inteira é calcular dois grandes números de Fibonacci consecutivos e dividi-los. A razão entre os números de Fibonacci F 25001 e F 25000 , cada um mais de 5000 dígitos, os rendimentos de mais de 10.000 algarismos significativos de a proporção de ouro.
A proporção áurea φ foi calculada com uma precisão de vários milhões de dígitos decimais (seqüência A001622 em OEIS ). Alexis Irlande realizados cálculos e verificação dos primeiros 17.000 milhões dígitos.
Pirâmides
Ambas as pirâmides egípcios e aqueles matemáticas regularespirâmides quadradas que se parecem com eles podem ser analisadas no que respeita à razão de ouro e outros rácios.
Pirâmides matemáticos e triângulos
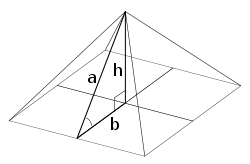
Uma pirâmide em que o apótema (altura inclinada ao longo da bissectriz de um rosto) é igual a φ vezes a semi-base (metade da largura da base) é às vezes chamado de pirâmide dourada . O triângulo isósceles que é a cara de um tal pirâmide pode ser construído a partir de duas metades de um retângulo de ouro dividida na diagonal (de tamanho semi-base, apótema), juntando-se as bordas de comprimento médio para fazer a apótema. A altura desta pirâmide é  vezes a semi-base (isto é, a inclinação da face é
vezes a semi-base (isto é, a inclinação da face é  ); o quadrado da altura é igual à área de uma face, φ vezes o quadrado da semi-base.
); o quadrado da altura é igual à área de uma face, φ vezes o quadrado da semi-base.
O medialdireito triângulo da pirâmide "de ouro" (veja a figura), com lados é interessante em seu próprio direito, demonstrando através doteorema de Pitágorasa relação
é interessante em seu próprio direito, demonstrando através doteorema de Pitágorasa relação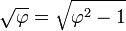 ou
ou 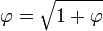 . Este " Kepler triângulo "é a única proporção triângulo com comprimentos de ponta emprogressão geométrica, assim como o 3-4-5 triângulo é a única proporção triângulo com comprimentos das arestas emprogressão aritmética. O ângulo de tangente
. Este " Kepler triângulo "é a única proporção triângulo com comprimentos de ponta emprogressão geométrica, assim como o 3-4-5 triângulo é a única proporção triângulo com comprimentos das arestas emprogressão aritmética. O ângulo de tangente corresponde ao ângulo que o lado da pirâmide faz com respeito ao chão, ... 51,827 graus (51 ° 49 ' 38 ").
corresponde ao ângulo que o lado da pirâmide faz com respeito ao chão, ... 51,827 graus (51 ° 49 ' 38 ").
Uma forma de pirâmide quase semelhante, mas com proporções racionais, é descrito no papiro Rhind (a fonte de uma grande parte de antigo conhecimento moderno de matemática do Egipto), com base na 3: 4: 5 triângulo; a encosta face correspondente ao ângulo da tangente com 4/3 é de 53,13 graus (53 graus e 8 minutos). A altura inclinada ou apótema é 5/3 ou 1.666 vezes a ... semi-base. O papiro de Rhind tem outro problema da pirâmide, bem como, novamente com inclinação racional (expresso como prazo sobre a ascensão). Matemática egípcia não incluem a noção de números irracionais, ea inclinação inversa racional (run / ascensão, multiplicado por um factor de 7 a converter a suas unidades convencionais de palmas por côvado) foi utilizado na construção de pirâmides.
Outra pirâmide matemático com proporções quase idênticos ao "de ouro" é aquele com perímetro igual a 2π vezes a altura, ou h: b = 4: π. Este triângulo tem um ângulo de face de 51,854 ° (51 ° 51 '), muito próximo a 51,827 ° da Kepler triângulo. pirâmide Esta relação corresponde à relação de coincidência  .
.
Pirâmides egípcias muito próximos na proporção dessas pirâmides matemáticos são conhecidos.
Pirâmides egípcias
Em meados do século XIX, Röber estudou várias pirâmides egípcias, incluindo Khafre, Menkaure e alguns dos Giza, Sakkara, e grupos de Abusir, e foi interpretada como tendo dito que a metade da base do lado da pirâmide é a média meio do lado , formando o que outros autores identificados como o triângulo Kepler; muitas outras teorias matemáticas da forma das pirâmides também têm sido explorados.
Uma pirâmide egípcia é notavelmente perto de uma "pirâmide dourada" -o grande pirâmide de Giza (também conhecida como a Pirâmide de Quéops ou Khufu). Sua inclinação de 51 ° 52 'é extremamente perto do "ouro" pirâmide inclinação de 51 ° 50' e baseada no π pirâmide inclinação de 51 ° 51 '; outras pirâmides de Gizé (Quéfren, 52 ° 20 ', e Miquerinos, 50 ° 47') também estão muito perto. Se a relação com a proporção áurea nessas pirâmides é por design ou por acidente permanece aberto à especulação. Várias outras pirâmides egípcias são muito perto do racional 3: 4: 5 forma.
Adicionando combustível à controvérsia sobre a autoria arquitetônico da Grande Pirâmide,Eric Temple Bell, matemático e historiador, afirmou em 1950 que a matemática egípcia não teria apoiado a capacidade de calcular a altura inclinada das pirâmides, ou a relação com a altura, excepto no caso do 3: 4: 5 pirâmide, uma vez que o 3: 4: 5 triângulo era a única triângulo conhecido aos egípcios e eles não sabiam o teorema de Pitágoras, nem qualquer forma de raciocinar sobre irracionais tais como π ou φ .
Michael Rice, afirma que as autoridades principais sobre a história da arquitetura egípcia têm argumentado que os egípcios estavam bem familiarizados com a proporção áurea e que é parte da matemática das Pirâmides, citando Giedon (1957). Os historiadores da ciência sempre se debateu se os egípcios tinham qualquer conhecimento ou não, alegando que, em vez de sua aparência em um edifício egípcio é o resultado do acaso.
Em 1859, o pyramidologist John Taylor reivindicou que, na grande pirâmide de Giza , a proporção de ouro é representado pela razão entre o comprimento da face (a altura de inclinação), inclinado segundo um ângulo θ para o chão, a metade do comprimento do lado da base quadrada, equivalente ao secante do θ ângulo. Os dois comprimentos acima foram cerca de 186,4 e 115,2 metros respectivamente. A proporção destes comprimentos é a proporção de ouro, com uma precisão de mais dígitos do que qualquer uma das medições originais. Da mesma forma, Howard Vyse, de acordo com Matila Ghyka, relatou a grande altura da pirâmide 148,2 m, e uma meia-base de 116,4 m, dando origem a 1,6189 para a relação entre altura inclinada a meia-base, novamente mais preciso do que a variabilidade dos dados.
Observações contestadas
Exemplos de observações controvertidas da proporção áurea incluem o seguinte:
- O historiador John Homem declara que as páginas da Bíblia de Gutenberg foram "baseado na forma da seção de ouro". No entanto, de acordo com medições próprias do homem, a proporção entre a altura ea largura foi de 1,45.
- Algumas proporções específicas nos corpos de muitos animais (incluindo humanos) e partes de conchas de moluscos e cefalópodes são muitas vezes alegou ser em proporção áurea. Há uma grande variação nas medidas reais destes elementos em indivíduos específicos, no entanto, e a proporção em causa é muitas vezes significativamente diferente da proporção de ouro. A razão de sucessivas ossos falanges dos dedos e do osso metacarpo foi dito para aproximar a relação dourada. O shell Nautilus, cuja construção prossegue em uma espiral logarítmica, é frequentemente citado, geralmente com a idéia de que qualquer espiral logarítmica está relacionada com a proporção áurea, mas às vezes com a alegação de que cada nova câmara é proporcionado pela proporção áurea em relação ao anterior; no entanto, as medidas de escudos do nautilus não apoiar esta reivindicação.
- As proporções dos diferentes componentes de plantas (número de folhas para ramos, diâmetros de figuras geométricas dentro flores) são frequentemente reivindicado para mostrar a relação de proporção áurea em várias espécies. Na prática, existem variações significativas entre os indivíduos, as variações sazonais, variações de idade e nestas espécies. Enquanto a proporção de ouro pode ser encontrado em algumas proporções em alguns indivíduos em determinados momentos em seus ciclos de vida, não há nenhuma relação consistente em suas proporções.
- Em investir, alguns profissionais de análise técnica usa a proporção áurea para indicar apoio de um nível de preços, ou resistência a aumentos de preços, de uma ação ou commodity; depois do preço significativo muda para cima ou para baixo, novos níveis de suporte e resistência são supostamente encontrada em ou perto de preços relacionados com o preço de partida através da proporção áurea. O uso da proporção áurea em investir também está relacionada com padrões mais complicados descritas por números de Fibonacci (por exemplo, princípio onda Elliott e Fibonacci). No entanto, outros analistas de mercado publicaram análises que sugerem que estas percentagens e padrões não são suportadas pelos dados.
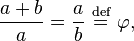
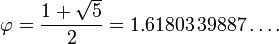

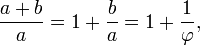
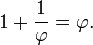

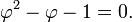
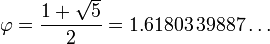

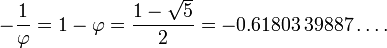
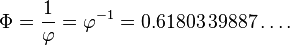
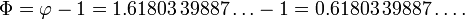
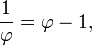
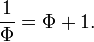
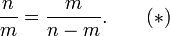
![\ Varphi = [1; 1, 1, 1, \ pontos] = + 1 \ cfrac {1} {1 + \ cfrac {1} {1 + \ cfrac {1} {1 + \ ddots}}}](../../images/2794/279449.png)
![\ Varphi ^ {- 1} = [0; 1, 1, 1, \ pontos] = 0 + \ cfrac {1} {1 + \ cfrac {1} {1 + \ cfrac {1} {1 + \ ddots}}}](../../images/2794/279450.png)
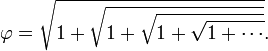

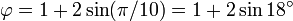
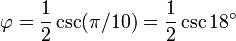


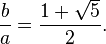



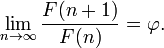

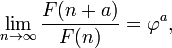
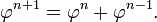
![\ Begin {align} 3 \ varphi ^ 3-5 \ varphi ^ 2 + 4 = & 3 (\ varphi ^ 2 + \ varphi) - 5 \ varphi ^ 2 + 4 = \\ & 3 [(\ varphi + 1) + \ varphi] - 5 (\ varphi + 1) + 4 \\ & = \ varphi + 2 \ approx 3,618. \ End {align}](../../images/2795/279500.png)
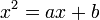
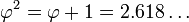

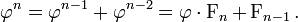
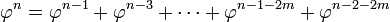

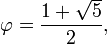
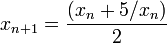
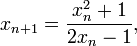
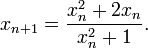
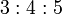 e
e 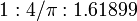 são de interesse particular em relação ao pirâmides egípcias.
são de interesse particular em relação ao pirâmides egípcias. 