Teorema

A imagem matemática pinta mil palavras: o teorema de Pitágoras .

Em lógica matemática, um teorema é um tipo de abstrato objeto, um prova de que é um fórmula de um linguagem formal, que pode ser derivada a partir da regras do sistema formal que é aplicado à linguagem formal; outro sinal de que é uma declaração em linguagem natural, que pode ser comprovado com base em pressupostos explicitamente declarados ou previamente acordados.

Em todas as configurações, uma propriedade essencial de teoremas é que eles são deriváveis através de um conjunto fixo de regras de inferência e axiomas sem quaisquer pressupostos adicionais. Isto não é uma questão de o semântica da linguagem: a expressão de que resulta a partir de uma derivação é um consequência sintática de todas as expressões que o precedem. Em matemática , a derivação de um teorema é muitas vezes interpretado como uma prova da verdade da expressão resultante, mas diferente sistemas de dedução pode originar outras interpretações, dependendo dos significados dos regras de derivação.

As provas de teoremas tem dois componentes, o chamado hipóteses e o conclusões. A prova de um teorema matemático é um argumento lógico que demonstra que as conclusões são uma consequência necessária das hipóteses, no sentido de que se as hipóteses são verdadeiras, em seguida, as conclusões também devem ser verdadeiras, sem quaisquer outras suposições. O conceito de um teorema é portanto fundamentalmente dedutivo, em contraste com a noção de um científica teoria, que é empírica.

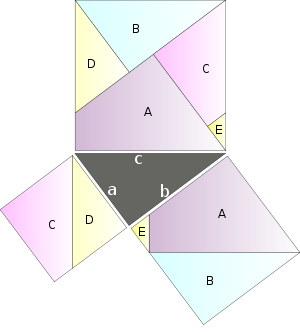
Embora eles podem ser escritos em um completamente forma simbólica, teoremas são muitas vezes expressa em uma linguagem natural, como Inglês. O mesmo é verdade das provas, que são muitas vezes expressas como logicamente organizado e claramente redigido argumentos informais destinadas a demonstrar que uma prova simbólica formal pode ser construído. Tais argumentos são tipicamente mais fácil de verificar que não os puramente simbólicas - na verdade, muitos matemáticos que expressam uma preferência por uma prova de que não só demonstra a validade de um teorema, mas também explica de alguma forma por que é obviamente verdadeiro. Em alguns casos, uma imagem por si só pode ser suficiente para provar um teorema.

Porque teoremas estão no cerne da matemática, eles também são fundamentais para a sua estética. Teoremas são freqüentemente descritos como sendo "trivial", ou "difícil", ou "profundo", ou mesmo "bonita". Estes julgamentos subjetivos variam não só de pessoa para pessoa, mas também com o tempo: por exemplo, como uma prova é simplificado ou melhor compreendida, um teorema que já foi difícil pode tornar-se trivial. Por outro lado, um teorema profundo pode ser simplesmente declarou, mas sua prova pode envolver conexões surpreendentes e sutis entre áreas diferentes da matemática. O último teorema de Fermat é um exemplo particularmente bem conhecido de um tal teorema.

Noções formais e informais

Logicamente a maioria dos teoremas são da forma de uma indicativa condicional:., se A, então B Tal teorema não afirma que B é sempre verdadeiro, mas apenas que B deve ser verdadeiro se A é verdadeiro. Neste caso, um é chamado o hipótese do teorema (note que "hipótese" aqui é algo muito diferente de um conjectura) e B a conclusão. O teorema "Se n é um mesmo número natural , então n / 2 é um número natural "é um exemplo típico, no qual a hipótese é que n é um número natural e mesmo a conclusão é que n / 2 é também um número natural.

A fim de ser provado, um teorema deve ser expresso como, uma declaração formal preciso. No entanto, teoremas são geralmente expressos em linguagem natural, em vez de uma forma completamente simbólico, com a intenção de que o leitor será capaz de produzir uma declaração formal do informal. Além disso, há muitas vezes hipóteses que são entendidos no contexto, em vez do que explicitamente indicado.

É comum em matemática para escolher um número de hipóteses que são assumidos para ser verdade dentro de uma determinada teoria, e, em seguida, declarar que a teoria consiste de todos os teoremas demonstráveis usando essas hipóteses como suposições. Neste caso, as hipóteses que formam a base fundamental são chamados a axiomas (ou postulados) da teoria. O campo da matemática conhecido como teoria da prova estuda sistemas axiomáticos formais e as provas que podem ser executadas dentro deles.

A planar mapa com cinco cores de modo que não há duas regiões com a mesma cor se encontram. Na verdade, pode ser colorida, desta forma, com apenas quatro cores. O teorema de quatro cores afirma que tais corantes são possíveis para qualquer mapa planar, mas cada prova conhecida envolve uma pesquisa computacional que é muito longo para verificar a mão.

Alguns teoremas são "trivial", no sentido de que eles seguem a partir de definições, axiomas e teoremas em outras maneiras óbvias e não contêm qualquer insights surpreendentes. Alguns, por outro lado, pode ser chamado de "profunda": suas provas pode ser longo e difícil, envolver áreas da matemática superficialmente distinta da declaração do próprio teorema, ou mostrar surpreendentes conexões entre áreas diferentes da matemática. Um teorema pode ser simples para estado e ainda ser profundo. Um excelente exemplo é Último Teorema de Fermat , e há muitos outros exemplos de teoremas ainda profundas simples em teoria dos números e combinatória , entre outras áreas.

Há outros teoremas para que uma prova é conhecida, mas a prova não pode ser facilmente escrito. Os exemplos mais proeminentes são o teorema de quatro cores ea Kepler conjectura. Ambos os teoremas só são conhecidos por ser verdade, reduzindo-os a uma pesquisa computacional que depois é verificada por um programa de computador. Inicialmente, muitos matemáticos não aceitou esta forma de prova, mas tornou-se mais amplamente aceito nos últimos anos. O matemático Doron Zeilberger tem mesmo ido tão longe como a alegação de que estes são, possivelmente, os únicos resultados não triviais que os matemáticos já provadas. Muitos teoremas matemáticos podem ser reduzidos a computação mais simples, incluindo identidades polinomiais, identidades trigonométricas e identidades hipergeométrica.

Relação à prova

A noção de um teorema é profundamente interligados com o conceito de prova. Com efeito, teoremas são verdadeiras precisamente no sentido de que eles possuem provas. Portanto, para estabelecer um enunciado matemático como um teorema, a existência de uma linha de raciocínio a partir de axiomas no sistema (e outros, teoremas já estabelecidas) a declaração dada deve ser demonstrada.

Embora a prova é necessária para produzir um teorema, que não é normalmente considerado parte do teorema. E apesar de mais de uma prova pode ser conhecido por um único teorema, apenas uma prova é necessário para estabelecer a validade do teorema. O teorema de Pitágoras ea lei do reciprocidade quadrática são candidatos ao título do teorema com o maior número de provas distintas.

Teoremas em lógica

Lógica , especialmente no campo da teoria da prova, considera teoremas como declarações (chamados de fórmulas ou fórmulas bem formadas) de um linguagem formal. Um conjunto de regras de dedução, também chamados de regras de transformação ou um gramática formal, deve ser fornecido. Estas regras de dedução dizer exatamente quando uma fórmula pode ser derivada de um conjunto de premissas.

Diferentes conjuntos de regras de derivação dar origem a diferentes interpretações do que significa para uma expressão a ser um teorema. Algumas regras de derivação e linguagens formais têm a intenção de capturar o raciocínio matemático; os exemplos mais comuns usar lógica de primeira ordem . Outros sistemas dedutivos descrever reescrita prazo, tais como as regras de redução para cálculo λ.

A definição de teoremas como elementos de uma linguagem formal permite resultados em teoria da prova que estudam a estrutura das provas formais ea estrutura das fórmulas demonstráveis. O resultado mais famoso é Teorema da incompletude de Gödel; representando teoremas sobre a teoria dos números básicos como expressões em uma linguagem formal, e, em seguida, representando esta linguagem em si mesma teoria dos números, Gödel construídos exemplos de declarações que não são nem demonstráveis nem refutável de axiomatizações da teoria dos números.

Relação com as teorias científicas

Teoremas em matemática e teorias da ciência são fundamentalmente diferentes em sua epistemologia. Uma teoria científica não pode ser provada; o seu atributo principal é que é refutável, ou seja, ele faz previsões sobre o mundo natural que são testáveis por experimentos. Qualquer divergência entre a previsão e experiência demonstra a incorreção da teoria científica, ou pelo menos limita sua precisão ou domínio de validade. Teoremas matemáticos, por outro lado, são puramente declarações formais abstratos: a prova de um teorema não pode envolver experiências ou outra evidência empírica da mesma forma tais evidências são utilizados para apoiar as teorias científicas.

A conjectura de Collatz: uma maneira de ilustrar a sua complexidade é estender a iteração dos números naturais aos números complexos. O resultado é um fractal, que (de acordo com universalidade) assemelha-se ao conjunto de Mandelbrot .

No entanto, existe um certo grau de empirismo e coleta de dados envolvido na descoberta de teoremas matemáticos. Ao estabelecer um padrão, às vezes com o uso de um computador poderoso, os matemáticos podem ter uma idéia do que para provar, e em alguns casos até mesmo um plano de como começou a fazer a prova. Por exemplo, a Collatz conjectura foi confirmada pelos valores iniciais para cerca de 2,88 × 10 ^18. O Hipótese de Riemann foi verificado para os primeiros 10 trilhões de zeros da função zeta. Nenhuma dessas afirmações é considerado para ser provado.

Tais provas não constitui prova. Por exemplo, a Mertens conjectura é uma afirmação sobre números naturais que agora é conhecido por ser falsa, mas nenhum contra-exemplo explícito (isto é, um número natural n para o qual a função M Mertens (n) for igual ou superior a raiz quadrada de n) é conhecido: todos os números menos do que 10 ¹⁴ têm a propriedade Mertens, e o menor número que não tem esta propriedade só é conhecido por ser menor do que o exponencial de 1,59 x 10 ^40, que é de aproximadamente 10 para a alimentação de 4,3 x 10 ^39. Uma vez que o número de partículas no universo é geralmente considerado como sendo inferior a 10 para a alimentação 100 (um googol), não há esperança de encontrar um contra-exemplo explícito por busca exaustiva no presente.

Note-se que a palavra "teoria" também existe em matemática, para designar um conjunto de axiomas matemáticos, definições e teoremas, como, por exemplo, a teoria do grupo . Há também "teoremas" em ciência, especialmente a física, e em engenharia, mas muitas vezes eles têm demonstrações e provas em que premissas físicas e intuição desempenham um papel importante; os axiomas físicas em que tais "teoremas" se baseiam são eles próprios falsificável.

Terminologia

Teoremas são muitas vezes indicado por vários outros termos: o rótulo de "teorema" real está reservado para os resultados mais importantes, enquanto que os resultados que são menos importantes, ou distinto de outras formas, são nomeados por uma terminologia diferente.

• A proposição é uma declaração não associada a qualquer teorema particular. Este termo denota uma declaração às vezes com uma simples prova.
• A lema é "um pré-teorema", uma declaração que faz parte da prova de um teorema maior. A distinção entre teoremas e lemas é bastante arbitrário, uma vez que um matemático principal resultado é outro é menor reclamação. Lema de Gauss e Lema de Zorn, por exemplo, são interessantes o suficiente para que alguns autores apresentam o lema nominal, sem passar a usá-lo na prova de um teorema.
• A corolário é uma proposta que se segue, com pouca ou nenhuma prova de um teorema ou outra definição. Ou seja, proposição B é um corolário de uma proposição A se B pode ser facilmente deduzida a partir A.
• A alegação é um resultado necessário ou de forma independente interessante que pode ser parte da prova de outra instrução. Apesar do nome, as reclamações devem ser provada.

Existem outros termos, menos comumente utilizados, que são convencionalmente ligados a declarações comprovadas, de modo que certos teoremas são referidos por nomes históricos ou habituais. Para exemplos:

• Identidade, usado para teoremas que declaram uma igualdade entre duas expressões matemáticas. Exemplos incluem a identidade de Euler e A identidade de Vandermonde.
• Regra, utilizado para certos teoremas, como A regra de Bayes e Regra de Cramer, que estabelecem fórmulas úteis.
• Lei. Exemplos incluem o lei dos grandes números, a lei dos cossenos, e Zero uma lei de Kolmogorov.
• Princípio. Exemplos incluem Princípio de Harnack, a menos princípio limite superior, eo pigeonhole princípio.
• A Inverso é um teorema inversa. Por exemplo, se um teorema indica que A é um relacionada com B, que é inversa iria indicar que B está relacionada com A. O inverso de um teorema não necessita de ser sempre verdade.

Alguns teoremas bem conhecidas têm até mesmo nomes mais idiossincráticos. O divisão algoritmo um teorema que expressa o resultado da divisão dos números naturais e anéis mais gerais. O Paradoxo de Banach-Tarski é um teorema em medir a teoria de que é paradoxal no sentido de que ela contradiz intuições comuns sobre o volume no espaço tridimensional.

Uma declaração não comprovada de que é acreditado para ser verdade é chamado de conjectura (ou às vezes um hipótese, mas com um significado diferente do que foi discutida acima). Para ser considerada uma conjectura, uma declaração deve normalmente ser proposto publicamente, altura em que o nome do proponente pode ser anexado à conjectura, como acontece com a conjectura de Goldbach . Outros conjecturas famosos incluem o Collatz conjectura ea Hipótese de Riemann.

Traçado

Um teorema e sua prova normalmente são definidos da seguinte forma:

Teorema (nome da pessoa que provou isso e ano de descoberta, prova ou publicação).

Demonstração do teorema.

Proof.

Descrição da prova.

A fim de a prova pode ser assinalada pelas letras QED significado " quod erat demonstrandum "ou por um dos lápide marcas "□" ou "∎", que significa "End of Proof", introduzido pela Paul Halmos na sequência da sua utilização em artigos de revistas.

O estilo exato dependerá do autor ou publicação. Muitas publicações fornecem instruções ou macros para composição no estilo de casa.

É comum que um teorema a ser precedido por definições descrevem o significado exacto dos termos utilizados no teorema. Também é comum para um teorema a ser precedido por uma série de proposições ou lemas que são então usados na prova. No entanto, lemas são, por vezes, incorporado na prova de um teorema, seja com provas aninhados, ou com suas provas apresentadas após a prova do teorema.

Corolários um teorema ou são apresentadas entre o teorema ea prova, ou diretamente após a prova. Às vezes corolários tem provas de seu próprio que explicam por que eles seguem a partir do teorema.

Erudição

Estima-se que mais de um quarto de um milhão de teoremas são provadas a cada ano.

O bem-conhecido aforismo, "Um matemático é um dispositivo para transformar o café em teoremas", é provavelmente devido a Alfréd Rényi, embora seja muitas vezes atribuída a colega de Rényi Paul Erdős (e Rényi pode ter sido pensando em Erdős), que era famoso por muitos teoremas ele produzidos, o número de suas colaborações, e seu hábito de beber café.

O classificação dos grupos finitos simples é considerada por alguns como a prova mais longa de um teorema; que compreende dezenas de milhares de páginas em 500 artigos de revistas por cerca de 100 autores. Esses papéis estão juntos acreditado para dar uma prova completa, e há vários projetos em andamento para reduzir e simplificar esta prova.

Procurar teorema em Wiktionary, o dicionário livre.