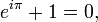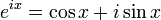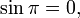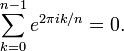A identidade de Euler

A partir de E = 1 ^0, viajando a uma velocidade de i uma em relação à posição do para o período de tempo π, e adição de 1, chega-se a 0. (O esquema é um diagrama de Argand )

Em análise matemática , a identidade de Euler, em homenagem a Leonhard Euler , é a equação

onde

é Número de Euler, a base do logaritmo natural,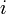

representa a unidade imaginária , um dos dois números complexos cuja quadrado é um negativo (o outro está ), E

é pi , a razão entre a circunferência de um círculo com o seu diâmetro.

A identidade de Euler também é chamado às vezes a equação de Euler.

Natureza da identidade

A identidade de Euler é considerado por muitos para ser notável pela sua beleza matemática. Três básicas de aritmética operações ocorrem exatamente uma vez cada: adição , multiplicação e exponenciação . A identidade também links cinco fundamentais constantes matemáticas:

• O número 0 .
• O número 1 .
• O número π , que é onipresente em trigonometria , geometria do espaço euclidiano , e análise matemática .
• O número e, a base de logaritmos naturais , que ocorre amplamente em análise matemática (e ≈ 2,71828).
• O i número , unidade imaginária dos números complexos , que contêm as raízes de todos os polinômios nonconstant e levar a visão mais profunda muitos operadores, tais como a integração .

Além disso, na análise matemática, equações são vulgarmente escritas com de zero de um dos lados.

Percepções da identidade

Uma pesquisa conduzida pelo leitor Mathematical Intelligencer chamado a identidade como a mais bela teorema na matemática. Outra pesquisa conduzida pelo leitor Physics World, em 2004, chamado A identidade de Euler a "maior equação que nunca", juntamente com as equações de Maxwell .

O livro Dr. A fórmula de Euler Fabulous [2006], de Paul Nahin (Professor Emérito da Universidade de New Hampshire), é dedicado à identidade de Euler; é 400 páginas. O livro afirma que a identidade define "o padrão ouro para beleza matemática."

Constance Reid afirmou que a identidade de Euler foi "a fórmula mais famosa em toda a matemática."

Gauss é relatada a ter comentado que, se essa fórmula não foi imediatamente aparente a um estudante em ser dito que, o aluno nunca seria um matemático de primeira classe.

Depois de provar a identidade em uma palestra, Benjamin Peirce, uma observou século XIX matemático e Professor de Harvard, disse: "É absolutamente paradoxal, não podemos compreendê-lo, e nós não sabemos o que isso significa, mas temos provado isso, e, portanto, sei que deve ser a verdade."

Professor de matemática de Stanford Keith Devlin diz, "como um soneto shakespeariano que capture a essência do amor, ou uma pintura que traga para fora a beleza do formulário humano que é muito mais do que apenas pele profunda, a equação de Euler desce às profundezas da existência."

Derivação

Fórmula de Euler para um ângulo geral.

A identidade é um caso especial de Fórmula de Euler de análise complexa, que afirma que

para qualquer número real x. (Observe que os argumentos para o trigonométricas funções seno e cosseno são tomadas para estar em radianos .) Em particular, se

em seguida

Desde

e

segue que

o que dá a identidade

Generalização

A identidade de Euler é um caso especial de a identidade mais geral de que a n-ésima raízes da unidade, para n> 1, somar a 0:

A identidade de Euler é o caso em que n = 2.

Atribuição

Enquanto Euler escreveu sobre sua fórmula relacionando e para cos e termos pecado, não há registro conhecido de Euler de fato afirmando ou decorrentes da própria identidade equação simplificada; Além disso, a fórmula foi provavelmente conhecido antes de Euler. Assim, a questão de haver ou não a identidade deve ser atribuída a Euler não é atendida.