
1 (número)
Fundo para as escolas Wikipédia
Os artigos desta seleção Escolas foram organizados por tópico currículo graças a voluntários Crianças SOS. Com SOS Children você pode escolher para patrocinar crianças em mais de cem países
1 | |
-1 0 1 2 3 4 5 6 7 8 9 → Lista dos números - Inteiros 0 10 20 30 40 50 60 70 80 90 → | |
| Cardeal | 1 um |
| Ordinal | 1 primeiro |
| Sistema de numeração | unary |
| Fatoração | 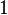 |
| Divisores | 1 |
| Numeral romano | EU |
| Numeral romano (Unicode) | Ⅰ, ⅰ |
| Árabe | 1 |
| Ge'ez | ፩ |
| Bengali | 1 |
| Numeral chinês | 一, 壹 |
| Devanāgarī | 1 |
| Hebraico | א ( Alef) |
| Khmer | 1 |
| Thai | 1 |
| prefixos | mono (a partir de grego ) uni- (de Latin ) |
| Binário | 1 |
| Octal | 1 |
| Duodecimal | 1 |
| Hexadecimal | 1 |
| Procurar um em Wiktionary, o dicionário livre. |
1 (um) é um número , numeral, e o nome do glyph que representa esse número. Ele representa uma única entidade. Uma é por vezes referido como unidade ou unidade como um adjectivo. Por exemplo, uma segmento de linha de "unidade de comprimento" é um segmento de linha de comprimento 1.
Em matemática, pode representar:
- Historicamente, o primeiro número de ordem , embora algumas convenções modernos usam 0 (número) como o primeiro ordinal
- o número natural seguinte 0 e precedendo 2, o multiplicativo identidade dos inteiros
- o correspondente número real 1, a identidade multiplicativa dos reais e números complexos
- em álgebra abstrata , é a identidade multiplicativa
Matemática
Para qualquer número x:
- · x 1 = 1 x = x · (1 é o multiplicativo de identidade)
- x = x / 1 (ver divisão )
- x = 1 x 1, x = 1, e para não nulos x, x 0 = 1 (veja exponenciação )
Usando ordinária disso , temos 1 + 1 = 2.
Não se pode ser usado como a base de um posicionamento de sistema numérico ; às vezes totalização é referida como "base de 1", uma vez que apenas uma marca (a contagem) é necessária, mas isto não é uma notação posicional.
O logaritmos base 1 é indefinido, uma vez que 1 x = 1 e portanto não tem única função inversa .
No número real do sistema, um pode ser representado de duas maneiras como um decimal recorrente: como 1.000 ... e como 0.999 ... (qv).
No Representação Von Neumann de números naturais, 1 é definido como o conjunto {0}. Este conjunto tem cardinalidade 1 e hereditários Ranking 1. Define como este com um único elemento são chamados singletons.
Em Principia Mathematica, um é definido como o conjunto de todos singletons.
Numa multiplicativo grupo ou monóide, o elemento de identidade é por vezes designado "1", mas de "e" (do alemão Einheit, unidade) é mais tradicional. No entanto, "1" é especialmente comum para a identidade de um multiplicativo anel. (Note-se que esta identidade multiplicativo é também muitas vezes chamado de "unidade".)
Uma é a sua própria fatorial , e o seu próprio quadrado e cubo (e assim por diante, como um × 1 × ... × 1 = 1). Um deles é o primeiro número figurado de todos os tipos, tais como número triangular, número pentagonal e centrado número hexagonal para citar apenas alguns.
Por causa da identidade multiplicativo, se f (x) é uma função multiplicativa, então f (1) deve ser igual a 1.
É também os primeiros e segundo números na Fibonacci sequência, e é o primeiro número em muitas sequências matemáticas. Por uma questão de convenção, Handbook início do Sloane de Sequências de Inteiros adicionou uma inicial de 1 a qualquer seqüência que já não tê-lo, e considerou estas 1 do iniciais na sua ordenação lexicográfica. Mais tarde Enciclopédia de Sloane de Sequências de Inteiros e sua contraparte Web, a Enciclopédia On-Line de Sequências de Inteiros , ignorar os iniciais na sua ordenação lexicográfica de sequências, porque tais pessoas muitas vezes iniciais correspondem a casos triviais.
Uma delas é a produto vazio.
Um deles é o menor número inteiro impar positivo.
Um deles é um número divisor harmônica.
Um deles é muitas vezes a representação interna do Boolean true constante em sistemas de computador.
Um não é nem um número primo nem um número de composto, mas uma unidade, como -1 e, no Inteiros de Gauss, [unidade imaginária | i]] e -I. O teorema fundamental da aritmética garante fatoração única sobre os inteiros somente até unidades (por exemplo, 4 = 2 2 = (-1) 4 × 1 × 23 2 2).
Um era anteriormente considerado nobre por alguns matemáticos, usando a definição que um primo é divisível apenas por um e ela própria. No entanto, isso dificulta o teorema fundamental da aritmética , assim definições modernas excluir unidades. A última profissional matemático para rotular publicamente 1 um número primo era Henri Lebesgue em 1899.
Um deles é um dos três valores possíveis do Função de Möbius: ela assume o valor um para inteiros quadrados livres com um número par de fatores primos distintos.
Um deles é o único número ímpar na gama de Função totient de Euler φ (x), nos casos x = 1 e x = 2.
Um deles é o único número de 1-perfeito (ver multiplique o número perfeito).
Por definição, uma é a magnitude ou valor absoluto de um e um vector de unidade matriz unitária (mais geralmente chamado uma matriz de identidade). Note-se que a matriz unidade termo é geralmente usado para significar algo um pouco diferente.
Um deles é o dígito de liderança mais comum em muitos conjuntos de dados, uma consequência da A lei de Benford.
Lista de cálculos básicos
| Multiplicação | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 50 | 100 | 1000 | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
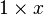 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 50 | 100 | 1000 |
| Divisão | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 | 1 | 0,5 | 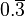 | 0,25 | 0,2 | 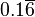 | 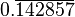 | 0,125 | 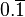 | 0,1 | 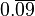 | 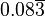 |
 |  | 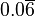 | |
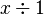 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| Exponenciação | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
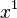 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
Evolução do glifo
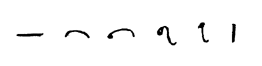
O glifo usado hoje no mundo ocidental para representar o número 1, uma linha vertical, muitas vezes com um serif no topo e às vezes uma pequena linha horizontal na parte inferior, traça as suas raízes de volta para os índios, que escreveu um como uma linha horizontal (em chinês hoje esta é a forma como está escrito). O Gupta escreveu-o como uma linha curva, eo Nagari adicionado às vezes um pequeno círculo à esquerda (rodado um quarto de volta para a direita, este 9-sósia tornou-se o dia atual número 1 no Gujarati e Os scripts Punjabi). O Nepali também rodado para a direita, mas manteve o círculo pequeno. Isso acabou se tornando o topo serif no numeral moderno, mas a linha horizontal curta ocasional na parte inferior provavelmente se origina de semelhança com o numeral romano I. Em alguns países europeus (por exemplo, Alemanha ) a pouco serif no topo é estendido às vezes em um longo curso ascendente, por vezes, enquanto a linha vertical, o que pode levar a confusões com o glifo para sete em outros países. Onde o 1 é escrito com um longo curso ascendente, o número 7 tem um curso horizontal através da linha vertical.
Embora a forma do carácter 1 tem uma ascender na mais moderna carácteres tipo, em caracteres tipográficos com texto figura o caráter geralmente é de -x altura, como, por exemplo, em ![]() .
.
