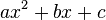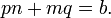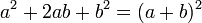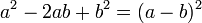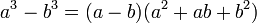Fatoração
Informações de fundo
Crianças SOS tentou tornar o conteúdo mais acessível Wikipedia por esta selecção escolas. Para comparar instituições de caridade de patrocínio esta é a melhor ligação de patrocínio .
Em matemática , fatoração (também em factorisation Britânica Inglês) ou factoring é a decomposição de um objecto (por exemplo, um número , um polinómio , ou uma matriz ) para um produto de outros objetos, ou fatores, que, quando multiplicados juntos dão o original. Por exemplo, o número 15 fatores em números primos como 3 × 5, e as polinomiais x 2-4 fatores como (x - 2) (x + 2). Em todos os casos, um produto de objectos mais simples é obtido.
O objetivo do factoring é geralmente para reduzir algo para "blocos básicos de construção", tais como números de números primos, ou polinômios para polinômios irredutíveis. Factoring inteiros é coberto pelo teorema fundamental da aritmética e factoring polinômios pelo teorema fundamental da álgebra.
O oposto de fatoração é expansão. Este é o processo de multiplicar juntamente factores para recriar o original, "expandidas" polinomial .
Fatoração inteiro para inteiros grandes parece ser um problema difícil. Não há nenhum método conhecido para realizá-lo rapidamente. Sua complexidade é a base da garantia assumida de alguns algoritmos de criptografia de chaves públicas, tais como RSA.
Uma matriz também pode ser fatorado em um produto de matrizes de tipos especiais, para uma aplicação em que essa forma é conveniente. Um grande exemplo disso usa um ortogonal ou matriz unitária, e um matriz triangular. Existem diferentes tipos: QR decomposição, LQ, QL, RQ, RZ.
Outro exemplo é o factorization de uma função de como a composição de outras funções que têm certas propriedades; por exemplo, cada função pode ser vista como a composição de um função surjective com um função injetora.
Fatoração Prime de um inteiro
Pelo teorema fundamental da aritmética , cada positivo inteiro tem um exclusivo fatoração em primos. Dado um algoritmo de fatoração por inteiro, pode levar qualquer inteiro até seus constituintes primos pela aplicação repetida deste algoritmo. Para grandes números, não eficiente algoritmo é conhecido. Para os números menores, no entanto, há uma variedade de algoritmos diferentes que podem ser aplicados.
Fatorar um polinômio quadrático
Qualquer polinomial quadrático sobre os números complexos (polinômios da forma 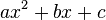 onde
onde  ,
,  E
E  ∈
∈  ) Pode ser tido em conta um expressão com a forma
) Pode ser tido em conta um expressão com a forma  usando a fórmula quadrática . O método é o seguinte:
usando a fórmula quadrática . O método é o seguinte:
onde 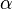 e
e  são os dois raízes do polinômio, encontradas com a fórmula quadrática .
são os dois raízes do polinômio, encontradas com a fórmula quadrática .
Polinômios factorável sobre os inteiros
Polinômios quadráticos às vezes podem ser tidos em conta dois binómios com coeficientes inteiros simples, sem a necessidade de usar a fórmula quadrática. Em uma equação quadrática , este irá expor as suas duas raízes. A fórmula
seriam tidos em conta:
onde
Você pode então definir cada binomial igual a zero e resolver para x para revelar as duas raízes. Factoring não envolve quaisquer outras fórmulas, e é na maior parte apenas algo que você vê quando você se depara com uma equação quadrática.
Tome, por exemplo, 2 x 2-5 x + 2 = 0. Devido a = 2 e Mn = a, Mn = 2, o que significa que de m e n, é 1 e o outro representa 2. Agora temos (2 x + p) (x + q) = 0. Como c = 2 e = pq pq C, = 2, o que significa que um de p e q é 1, um e o outro é 2 ou um representa 1 e o outro é - 2. A suposição e verificação de substituir o 1 e 2, e -1 e -2, em p e q (ao aplicar pn + mq = b) nos diz que 2 x 2-5 x + 2 = 0 em fatores (2 x - 1) (x - 2) = 0, dando-nos as raízes x = {0,5, 2}
Se um polinômio com coeficientes inteiros tem um discriminante que é um quadrado perfeito, que é polinomial factorável sobre os inteiros.
Por exemplo, olhe para o polinômio 2x 2 + 2x - 12. Se você substituir os valores da expressão para a fórmula quadrática, o discriminante 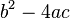 torna-se 2-4 fevereiro × 2 × -12, o que equivale a 100. 100 é um quadrado perfeito, então o polinômio 2x 2 + 2x - 12 é factorável sobre os inteiros; os seus factores são 2, (X - 2), e (x + 3).
torna-se 2-4 fevereiro × 2 × -12, o que equivale a 100. 100 é um quadrado perfeito, então o polinômio 2x 2 + 2x - 12 é factorável sobre os inteiros; os seus factores são 2, (X - 2), e (x + 3).
Agora olhe para o polinômio x 2 + 93x - 2. Seu discriminante, 93 2-4 × 1 × -2, é igual a 8657, que não é um quadrado perfeito. Então x 2 + 93x - 2 não pode ser tomada sobre os inteiros.
Perfeito trinômio quadrados

Alguns quadráticas podem ser tidos em conta dois binómios idênticos. Estes quadráticas são chamados perfeitos trinômio quadrados. Perfeito trinômio quadrados pode ser tido como segue:
Soma / diferença de dois quadrados
Outro tipo comum de factoring algébrica é chamado de diferença de dois quadrados. É a aplicação da fórmula
para quaisquer dois termos, quer sejam ou não são quadrados perfeitos. Se os dois termos são subtraídos, basta aplicar a fórmula. Se eles são adicionados, os dois binómios obtidos a partir do factoring terão cada um termo imaginário. Esta fórmula pode ser representada como
 .
.
Por exemplo, 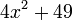 podem ser tidos em conta
podem ser tidos em conta  .
.
Factoring outros polinômios
Soma / diferença de dois cubos
Outra fórmula menos utilizado, mas ainda comum para factoring é a soma ou diferença de dois cubos. A soma pode ser representada pela
ea diferença por
Por exemplo, x 03-10 marco (ou x 3-1000) pode ser tido em conta em (x - 10) (x2 + x + 10 100).
Soma / diferença de dois números levantados para o mesmo poder
Em geral,  é um factor de
é um factor de 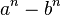 onde
onde  é um número inteiro positivo. Assim,
é um número inteiro positivo. Assim,
Além disso,  é um factor de
é um factor de 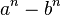 onde
onde  é um mesmo número inteiro positivo. De tal modo que,
é um mesmo número inteiro positivo. De tal modo que,
Da mesma forma,  é um factor de
é um factor de 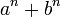 onde
onde  é um inteiro impar positivo. De modo que,
é um inteiro impar positivo. De modo que,
Factoring por agrupamento
Outra maneira de levar algumas equações é factoring pelo agrupamento. Isto é feito colocando os termos em uma expressão em dois ou mais grupos, em que cada grupo pode ser consignado por um método conhecido. Os resultados destes fatorações pode por vezes ser combinados para fazer uma expressão ainda mais simplificado.
Por exemplo, suponha que você tinha a expressão
que à primeira vista se parece com uma expressão de difícil controle. Um passo lógico, se você decidir levar por agrupamento, seria combinar todas as expressões com 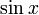 e tudo isto sem
e tudo isto sem 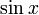 . Então você teria a expressão
. Então você teria a expressão
onde cada um dos dois grupos podem ser tidos dando
Isso pode ser ainda mais simplificada em
quando pode, então, ser tidos em conta
e finalmente
que é a expressão de forma plenamente integrado.
Outras fórmulas comuns
Existem muitas fórmulas adicionais que podem ser usados para levar facilmente um polinómio. Alguns dos mais comuns estão listados abaixo.
| Forma expandida | Forma fatorada |
|---|---|
 |  |
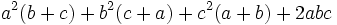 |  |
 | 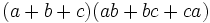 |
 | 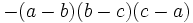 |
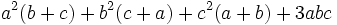 | 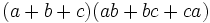 |
 | 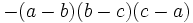 |
 |  |
 ( A identidade de Sophie Germain) ( A identidade de Sophie Germain) | 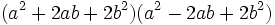 |
Factoring na lógica matemática
Em lógica matemática e automatizado prova de teoremas, o factoring é a técnica de derivar um único, mais específico átomo de uma disjunção de dois mais geral unificáveis átomos. Por exemplo, a partir de ∀ X, Y: P (x, a) ou P (b, Y) que podem derivar P (b, a).