Grupo cíclico

Em teoria grupo , um grupo cíclico ou um grupo monogenous é um grupo que pode ser gerado por um elemento único, no sentido em que o grupo tem um elemento g (chamado um " gerador "do grupo) de tal modo que, quando escrito multiplicativamente, todos os elementos do grupo é uma potência de g (um múltiplo de g quando a notação é aditivo).

Definição

Um grupo L é chamado cíclico se existe um elemento de g em G tal que G = <g> = {g ^{de n} | n é um número inteiro}. Uma vez que qualquer grupo gerado por um elemento de um grupo é um subgrupo deste grupo, que mostra que a única subgrupo de um grupo que contém L g L é em si suficiente para mostrar que G é cíclico.

Por exemplo, se G = g ^{{0, 1} g, ² g, ³ g, ⁴ g, ⁵ g} é um grupo, em seguida, ⁶ g g = ^0, e L é cíclico. Na verdade, G é essencialmente o mesmo que (isto é, isomorfo a) o conjunto {0, 1, 2, 3, 4, 5} com a adição de módulo 6. Por exemplo, 1 + 2 = 3 (mod 6) corresponde a ¹ g · g = ² g ^{de 3,} 2 e 5 + 1 = (mod 6) corresponde a ² g · g g ⁵ = ⁷ = g ^1, e assim por diante . Pode-se usar o φ isomorfismo definida por φ ⁽ⁱ g) = i.

Para cada inteiro positivo n há exatamente um grupo cíclico (até isomorfismo), cujo fim é n, e há exatamente um grupo cíclico infinito (os inteiros sob adição). Assim, os grupos cíclicos são os grupos mais simples e estão completamente classificado.

O nome 'cíclica' pode ser enganadora: é possível gerar um número infinito de elementos e não formam nenhum ciclos literais; isto é, cada 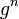é distinta. (Pode-se dizer que ele tem um ciclo infinitamente longo.) Um grupo gerado desta maneira é chamado um grupo cíclico infinito, e é isomorfo ao grupo aditivo de inteiros Z.

Uma vez que os grupos cíclicos são abelian, eles são muitas vezes escritos aditiva e denotado Z _n. No entanto, esta notação pode ser problemático para os teóricos dos números porque está em conflito com a notação usual para p número -adic anéis ou localização numa ideal nobre. O quociente notações Z / nZ, Z / N, e Z / (n) são alternativas convencionais. Nós adoptar a primeira delas aqui para evitar a colisão de notação. Veja também a seção Subgrupos e notação abaixo.

Pode-se escrever o grupo multiplicativo, e denotam que por C _n, em que n é a ordem (que pode ser ∞). Por exemplo, ⁴ g ^{de 3} g = ² g em C _5, ao passo que 3 + 4 = 2 em Z / 5 Z.

Propriedades

O teorema fundamental de grupos cíclicos que se afirma G é um grupo cíclico de ordem n, em seguida, cada subgrupo de G é cíclico. Além disso, a ordem de qualquer subgrupo de G é um divisor de n e para cada divisor k positivo de N o grupo L tem exactamente um subgrupo de ordem k. Este estabelecimento caracteriza grupos cíclicos finitas: um grupo de ordem n é cíclico se e somente se para cada divisor de n d o grupo tem no máximo um subgrupo de ordem d. Às vezes, a declaração equivalente é usado: um grupo de ordem n é cíclico se e somente se para cada divisor de n d o grupo tem exatamente um subgrupo de ordem d.

Cada grupo cíclico finito é isomorphic ao grupo {[0], [1], ..., [n - 1]} de inteiros módulo n sob disso, e qualquer grupo cíclico infinito é isomorfo a Z (o conjunto de todos os inteiros) sob adição. Assim, um só precisa de olhar para esses grupos para compreender as propriedades de grupos cíclicos em geral. Assim, os grupos cíclicos são um dos grupos mais simples para estudar e um número de propriedades agradáveis são conhecidos.

Dado um grupo cíclico G de ordem n (n pode ser infinito) e para cada g em L,

• G é abeliano; isto é, o seu funcionamento grupo é comutativo: gh = hg (para todos h em G). Isto é assim desde g + h mod n = h + g mod n.
• Se n é finito, então g = g ⁿ é ⁰ o elemento de identificação do grupo, desde que n = 0 mod n.
• Se n = ∞, então há exatamente dois geradores: ou seja, 1 e -1 para Z, e quaisquer outros mapeadas para eles sob um isomorfismo em outros grupos cíclicos infinitos.
• Se n é finito, então há exatamente φ (n) geradores onde φ é o Função phi de Euler
• Cada subgrupo de G é cíclico. Com efeito, cada subgrupo finito de G é um grupo de {0, 1, 2, 3, ... m - 1} com a adição de módulo m. E cada subgrupo infinito de G é m Z para algum m, que é bijective a (portanto isomorfo a) Z.
• G _n é isomorfo a Z / n Z ( grupo fator de Z sobre n Z) desde Z / nZ = {0 + n Z, Z 1 + n, n + 2 Z, + 3 N Z, Z 4 + n, ..., n - 1 + nZ } 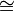{0, 1, 2, 3, 4, ..., n - 1} sob a adição módulo n.

De modo mais geral, se d é um divisor de n, então o número de elementos em Z / n que tem a ordem é φ d (d). O pedido da classe de resíduo de m é n / GCD (n, m).

Se p é um número primo , em seguida, o único grupo ( até isomorfismo) com elementos de P é o grupo cíclico C ou Z _p / p Z.

O produto directo de dois grupos cíclicos Z / N Z e Z / m Z é cíclico se e somente se n e m são coprime. Assim, por exemplo, Z / 12 Z é o produto directo de Z / 3 Z e Z / Z 4, mas não o produto directo de Z / 6 Z e Z / Z 2.

A definição implica imediatamente que grupos cíclicos têm muito simples apresentação do grupo C _∞ = <x |> e C _n = <x | x ^n> for finito n.

A grupo cíclico primário é um grupo com a forma Z / ^k p em que p é um número primo . O teorema fundamental de grupos abelianos afirma que cada finitamente gerado grupo abeliano é o produto direto de um número finito de grupos cíclicos e cíclicos infinitos primárias finitos.

Z / n Z e Z são também anéis comutativos . Se p é um primo, então Z / p Z é um campo finito, também denotado por F _p ou GF (p). Cada campo com p elementos é isomorphic a esta.

O unidades do anel Z / nZ são os números coprime a n. Eles formam um grupo sob multiplicação módulo n com elementos (ver acima) φ (n). É escrito como (Z / n Z) ^×. Por exemplo, podemos obter (Z / n Z) ^x = {1,5} quando n = 6, e obter (Z / n Z) ^x = {1,3,5,7} quando n = 8.

Na verdade, sabe-se que (Z / nZ) ^× é cíclico se e somente se n é 2 ou 4 ou p 2 ou ^k p ^k para uma impar número primo p e k ≥ 1, caso em que cada gerador de ácido (Z / nZ) ^× é chamado um modulo primitivo raiz n. Assim, (Z / nZ) ^× cíclico é para n = 6, mas não para n = 8, onde é em vez isomorfo ao Klein quatro grupo.

O grupo (Z / P Z) ^x é cíclico com p - 1 elementos para cada primo p, e também é escrito (Z / P Z) ^* porque consiste nos elementos diferentes de zero. Em termos mais gerais, todos os finito subgrupo do grupo multiplicativo de qualquer campo é cíclico.

Exemplos

Em 2D e 3D a grupo de simetria para n vezes de simetria rotacional é C _n, de grupo abstrato tipo Z _n. Em 3D também existem outros grupos de simetria que são algebricamente o mesmo, ver Grupos de simetria cíclico em 3D.

Note-se que o grupo S ¹ de todas as rotações de um círculo (o grupo círculo) não é cíclico, uma vez que não é ainda contável.

O ^n-ésimo raízes da unidade formar um grupo cíclico de ordem n sob a multiplicação. por exemplo, 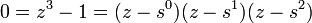onde e um grupo de sob a multiplicação é cíclica.

O Grupo de Galois de cada finito extensão de um campo campo finito é finita e cíclico; Por outro lado, dado um campo finito F e um grupo cíclico finito L, existe uma extensão finita de campo F cujo grupo L é de Galois.

Representação

O gráficos ciclo de grupos cíclicos finitos são todos os polígonos n -sided com os elementos nos vértices. O vértice escuro nos gráficos de ciclo abaixo representam o elemento de identidade, e os outros vértices são os outros elementos do grupo. Um ciclo consiste em sucessivas potências de qualquer um dos elementos ligados ao elemento de identidade.

C 1	C 2	C 3	C 4	C 5	C 6	C 7	C 8

O teoria da representação do grupo cíclico é um caso de base fundamental para a teoria da representação de grupos finitos mais gerais. No caso complexo, uma representação de um grupo cíclico se decompõe em uma soma direta de personagens lineares, fazendo a ligação entre a teoria caráter e teoria da representação transparente. No caso característica positiva, as representações indecomponíveis do grupo cíclico formar um modelo ea base indutiva para a teoria da representação de grupos com cíclico Subgrupos de Sylow e mais em geral a teoria da representação de blocos de defeito cíclico.

Subgrupos e notação

Tudo subgrupos e grupos de quociente de grupos cíclicos são cíclicos. Especificamente, todos os subgrupos de Z são da forma Z m, com m um inteiro ≥0. Todos estes subgrupos são diferentes, e para além do grupo trivial (para m = 0) são todos isomorfo a Z. O estrutura de subgrupos de Z é isomorfo ao dupla da estrutura dos números naturais ordenadas pela divisibilidade . Todos os grupos de factor de Z são finitas, excepto para o trivial excepção Z / {0} = Z / 0 Z. Para cada positivo d divisor de n, o grupo Z quociente / N Z tem precisamente um subgrupo de ordem d, o gerado pela classe resíduo de n / d. Não há outros subgrupos. A rede de subgrupos é, portanto, isomorphic para o conjunto de divisores de n, ordenados por divisibilidade. Em particular, é um grupo cíclico simples se e somente se sua ordem (o número de seus elementos) é primo.

Usando o grupo quociente formalismo, Z / nZ é uma notação padrão para o grupo cíclico com aditivo n elementos. Em terminologia anel, o subgrupo n Z é também o ideal (n), de modo que o quociente também pode ser escrito Z / (n) ou Z / n sem abuso de notação. Essas alternativas não entra em conflito com a notação para os números inteiros p -adic. A última forma tem a vantagem adicional de que ele lê da mesma maneira que o grupo ou anel é frequentemente descrito verbalmente, "Zee modificação en".

Como um problema prático, pode ser determinado um subgrupo C finito de ordem n, gerado por um elemento g, e pediu para encontrar o tamanho do subgrupo m gerado por g ^k por algum inteiro k. Aqui m será o menor número inteiro> 0 tal que mk é divisível por n. É, por conseguinte, n / m em que m = (k, n) é a mdc de k e n. Dito de outra forma, o índice do subgrupo gerado por g ^k é m. Este raciocínio é conhecido como o algoritmo de cálculo do índice, em teoria dos números .

Endomorfismos

O anel endomorphism do abeliano grupo Z / nZ é isomorfo a Z / N-se Z como um anel. Sob este isomorfismo, o número r corresponde à endomorphism de Z / n Z que mapeia cada elemento para a soma de R cópias do mesmo. Este é um bijection se e somente se r é primos entre si, com n, de modo a grupo automorphism de Z / nZ é isomorfa a unidade do grupo (Z / nZ) ^x (ver acima).

Do mesmo modo, o anel de endomorphism o grupo Z é isomorfa aditivo ao anel Z. O seu grupo automorphism é isomorfo para o grupo de unidades do anel Z, ou seja, {-1, 1} 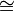C _2.

Praticamente grupos cíclicos

Um grupo é chamado praticamente cíclico se contiver um subgrupo cíclico de finita índice. Sabe-se que uma quantidade finita gerado grupo discreto com exactamente duas extremidades é praticamente cíclico. Cada subgrupo abeliano de um Gromov grupo hiperbólica é praticamente cíclico.