
Máximo divisor comum
Sobre este escolas selecção Wikipedia
Crianças SOS feita esta seleção Wikipedia ao lado de outras escolas recursos . Uma boa maneira de ajudar outras crianças é por patrocinar uma criança
Em matemática , o maior divisor comum (mdc), por vezes conhecido como o maior fator comum (GCF) ou fator comum mais alto (HCF), de dois diferentes de zero inteiros , é o maior inteiro positivo que divide ambos os números sem restante.
Visão global
A maior divisor comum de a e b é escrito como GCD (a, b), ou, por vezes, simplesmente como (a, b). Por exemplo, mdc (12, 18) = 6, gcd (-4, 14) = 2 e mdc (5, 0) = 5. Dois números são chamados coprime ou relativamente principais se seu maior divisor comum é igual a 1. Por exemplo, 9 e 28 são relativamente primos.
A maior divisor comum é útil para reduzir fracções vulgares ser Em termos mais baixo. Por exemplo, GCD (42, 56) = 14, portanto,
Calculando o mdc
O grande divisores comuns pode, em princípio, ser calculada através da determinação do fatorações principais dos dois números e comparando fatores, como no exemplo a seguir: para calcular mdc (18,84), encontramos os primos fatorações 18 = 2 · 3 2 e 84 = 2 2 · 3 · 7 e observe que a " sobreposição "das duas expressões é 2 · 3; então mdc (18,84) = 6. Na prática, este método só é viável para números muito pequenos; computação fatorações primos, em geral, leva muito tempo.
Um método muito mais eficiente é a Algoritmo de Euclides, que utiliza o algoritmo de divisão em combinação com a observação de que o mdc de dois números também divide a sua diferença: dividir 84 por 18 para obter um quociente de 4 e um resto de 12. Em seguida, dividir 18 por 12 para obter um quociente de 1 e um resto de 6 . Em seguida, divida 12 por 6 para obter um resto de 0, o que significa que 6 é o mdc.
A série de quocientes gerados pelo algoritmo de Euclides compor um fracção contínua.
Se a e b não são ambos zero, o maior divisor comum de a e b podem ser calculados usando menor múltiplo comum (LCM) de a e b:
Propriedades
- Cada divisor comum de a e b é um divisor de GCD (a, b).
- GCD (a, b), onde a e b não são ambos zero, pode ser definido em alternativa e de forma equivalente como o menor número inteiro positivo d qual pode ser escrito sob a forma d = A + B p · · q em que p e q são números inteiros . Esta expressão é chamada A identidade de Bézout. Números p e q como este pode ser calculado com a alargado algoritmo de Euclides.
- GCD (a, 0) = | a |, para a ≠ 0, uma vez que qualquer número é um divisor de 0, e o maior divisor é de um | a |. Isso geralmente é usado como cenário de base no algoritmo de Euclides.
- Se um divide o produto b · c, e GCD (a, b) = d, em seguida, a / d divide c.
- Se m é um número inteiro não negativo, então mdc (m ·, uma m · b) = m · mdc (a, b).
- Se m é um número inteiro, então GCD (a + b · m, b) = GCD (a, b). Se m é diferente de zero um divisor comum de a e b, em seguida, GCD (a / m, b / m) = GCD (a, b) / m.
- O mdc é um função multiplicativo da seguinte sentido: se um 1 e um 2 são relativamente primos, então GCD (a · 1 a 2, b) = GCD (a 1, b) · GCD (a 2, b).
- O mdc é um comutativa função: gcd (a, b) = mdc (b, a).
- O mdc é uma associativo função: gcd (a, mdc (b, c)) = mdc (mdc (a, b), c).
- O gcd de três números pode ser calculado como GCD (a, b, c) = GCD (GCD (a, b), c), ou de algum modo diferentes, aplicando commutativity e associamento. Isto pode ser estendido a qualquer número de números.
- GCD (a, b) está estreitamente relacionado com o menos lcm múltiplo comum (a, b): temos
- mdc (a, b) · lcm (a, b) = a · b.
- Esta fórmula é muitas vezes usado para calcular múltiplos menos comuns: um primeiro calcula o mdc com o algoritmo de Euclides e, em seguida, divide o produto dos números dados pela sua mdc. As seguintes versões do distributividade são verdadeiras:
- mdc (a, lcm (b, c)) = lcm (mdc (a, b), gcd (a, c))
- GCV (a, GCD (b, c)) = gcd (lcm (a, b), lcm (a, c)).
- É útil para definir GCD (0, 0) = 0 e LCM (0, 0) = 0, em seguida, porque os números naturais tornam-se um completo distributivo treliça com mdc como se encontram e LCM como operação de junção. Esta extensão da definição também é compatível com a generalização de anéis comutativos abaixo indicados.
- Em um sistema de coordenadas cartesianas , GCD (a, b) pode ser interpretado como o número de pontos com coordenadas integrais sobre a linha recta que une os pontos (0, 0) e (a, b), excluindo (0, 0).
Probabilidades e valor esperado
A probabilidade de que dois escolhidos aleatoriamente (ilimitado) inteiros 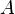 e
e 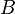 tem um determinado máximo divisor comum
tem um determinado máximo divisor comum 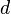 é
é 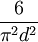 . Isso decorre da caracterização de
. Isso decorre da caracterização de  como o número inteiro
como o número inteiro 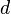 tal que
tal que 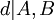 e
e  e
e 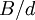 são primos entre si. A probabilidade de dois inteiros a partilha de um fator
são primos entre si. A probabilidade de dois inteiros a partilha de um fator 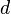 é
é 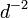 . A probabilidade de que dois inteiros são primos entre si é
. A probabilidade de que dois inteiros são primos entre si é 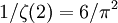 . (Ver coprime para uma derivação.)
. (Ver coprime para uma derivação.)
Usando essas informações, o valor esperado da maior função de divisor comum pode ser calculado. Isto é
Este último é o somatório Série harmônica, o que diverge. Por isso, o valor esperado do maior divisor comum das duas variáveis não é bem definida. Este não é o caso, em geral, no entanto. Para o maior divisor comum de 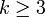 variáveis, o valor esperado é bem definida, e por o argumento anterior, é
variáveis, o valor esperado é bem definida, e por o argumento anterior, é
onde 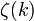 é o Função zeta de Riemann.
é o Função zeta de Riemann.
Para 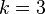 , Este é aproximadamente igual a 1,3684. Para
, Este é aproximadamente igual a 1,3684. Para 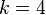 , É de aproximadamente 1,1106.
, É de aproximadamente 1,1106.
se todos os números inteiros x são limitados quanto 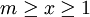 em seguida, os resultados podem ser estendidos para
em seguida, os resultados podem ser estendidos para
onde  é o Função zeta de Hurwitz.
é o Função zeta de Hurwitz.
se for diferente 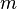 'S são conhecidas por diferentes
'S são conhecidas por diferentes  em seguida, o menor
em seguida, o menor 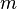 é feita.
é feita.
O mdc em anéis comutativos
O máximo divisor comum pode mais ser geralmente definido para elementos de um arbitrário anel comutativo .
Se R é um anel conmutativo, e a e b são, em R,, em seguida, um elemento de R d é chamado um divisor comum de a e b se divide tanto a e b (isto é, se existem elementos x e y em R tal que d · x = a e d · y = b). Se d for um divisor comum de a e b, e cada divisor comum de a e b divide a d, em seguida, d é chamado uma maior divisor comum de a e b.
Note que com esta definição, dois elementos a e b podem muito bem ter vários o maior divisor comum, ou mesmo nenhum. Mas, se o símbolo R representa um domínio integral em seguida, quaisquer dois de GCD de um e b deve ser elementos associados. Além disso, se o símbolo R representa um domínio fatoração única, então quaisquer dois elementos têm uma mdc. Se o símbolo R representa um Domínio euclidiana seguida, uma forma de o algoritmo de Euclides pode ser usado para calcular o maior divisor comum.
O que se segue é um exemplo de um domínio integral com dois elementos que não têm um mdc:
Os elementos 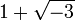 e
e 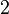 são dois divisores comuns "máximas" (ou seja, qualquer divisor comum que é um múltiplo de 2 está associada a 2, o mesmo é válido para
são dois divisores comuns "máximas" (ou seja, qualquer divisor comum que é um múltiplo de 2 está associada a 2, o mesmo é válido para 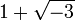 ), Mas eles não estão associados, por isso não há maior divisor comum de a e b.
), Mas eles não estão associados, por isso não há maior divisor comum de a e b.
Correspondente à propriedade Bezout podemos, em qualquer anel comutativo, considere a coleção de elementos do formulário 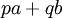 , Onde p e q gama sobre o anel. Isto é o ideal gerado por a e b, e é indicado simplesmente
, Onde p e q gama sobre o anel. Isto é o ideal gerado por a e b, e é indicado simplesmente 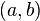 . Em um anel de todos cujos ideais são principais (a domínio de ideal principal ou PID), este ideal será idêntico com o conjunto de múltiplos de algum elemento anel d; em seguida, esta é uma d maior divisor comum de a e b. Mas o ideal
. Em um anel de todos cujos ideais são principais (a domínio de ideal principal ou PID), este ideal será idêntico com o conjunto de múltiplos de algum elemento anel d; em seguida, esta é uma d maior divisor comum de a e b. Mas o ideal 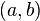 Pode ser útil, mesmo quando não há maior divisor comum de a e b. (Na verdade, Ernst Kummer utilizado este ideal como um substituto para uma mdc em seu tratamento de último teorema de Fermat , embora ele imaginou-a como conjunto de múltiplos de alguns hipotético ou ideal, elemento anel d, onde o termo anel de teoria.)
Pode ser útil, mesmo quando não há maior divisor comum de a e b. (Na verdade, Ernst Kummer utilizado este ideal como um substituto para uma mdc em seu tratamento de último teorema de Fermat , embora ele imaginou-a como conjunto de múltiplos de alguns hipotético ou ideal, elemento anel d, onde o termo anel de teoria.)
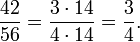
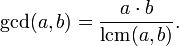

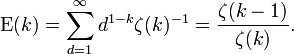

![R = \ mathbb {Z} \ left [\ sqrt {-3} \ right], \ quad a = 4 = 2 \ cdot 2 = \ left (1+ \ sqrt {-3} \ right) \ left (1- \ sqrt {-3} \ right), \ quad b = \ left (1+ \ sqrt {-3} \ right) \ cdot 2.](../../images/184/18487.png)
