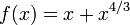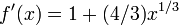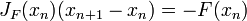El método de Newton

En análisis numérico, el método de Newton (también conocido como el Newton Raphson o el método de Newton-Fourier) es quizás el método más conocido para encontrar sucesivamente mejores aproximaciones a los ceros (o raíces) de un verdadero -valued función . El método de Newton a menudo puede converger con notable rapidez, especialmente si la iteración comienza la raíz "suficientemente cerca" deseado. ¿Qué tan cerca "lo suficientemente cerca" tiene que ser y lo rápido que "con notable rapidez" puede ser depende del problema, como se discute en detalle más adelante. Por desgracia, lejos de la raíz deseada, el método de Newton puede conducir fácilmente a un usuario incauto por mal camino, y el mal camino con poco aviso. Por lo tanto, buenas implementaciones del método de incrustar en una rutina que también detecta y tal vez supera los posibles fallos de convergencia.

El método de Newton también se puede utilizar para encontrar un mínimo o máximo de una función tal, mediante la búsqueda de un cero en la primera derivada de la función, ver El método de Newton como un algoritmo de optimización.

El algoritmo es el primero en la clase de Métodos de Householder, sucedido por Método de Halley.

Descripción del método

La idea del método es el siguiente: se empieza con una estimación inicial que está razonablemente cerca de la verdadera raíz, entonces la función se aproxima por su línea tangente (que puede ser calculado utilizando las herramientas de cálculo ), y uno calcula el x interceptación de esta línea tangente (que se hace fácilmente con álgebra elemental). Esto x interceptación será típicamente una mejor aproximación a la raíz de la función de la conjetura original, y el método puede ser reiteró.

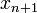Una ilustración de una iteración del método de Newton (la función f se muestra en azul y la línea tangente está en rojo). Vemos que es una mejor aproximación que 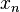para la raíz de la función de .

Supongamos que f: [a, b] → R es un diferenciable función definida en el intervalo [a, b] con valores en el números reales R. La fórmula para la convergencia en la raíz se puede derivar fácilmente. Supongamos que tenemos un poco de corriente aproximación x _n. Entonces podemos derivar la fórmula para una mejor aproximación, x _{n + 1} haciendo referencia a la figura de la derecha. Sabemos por la definición de la derivada en un punto dado que es la pendiente de la tangente en ese punto.

Esto es

.

Aquí, f 'denota la derivada de la función f. Luego de álgebra simple podemos derivar

.

Comenzamos el proceso con un poco de valor inicial arbitrario x _0. (Cuanto más cerca del cero, mejor. Pero, en ausencia de cualquier intuición acerca de donde el cero puede mentir, una "conjetura, y marca" método podría reducir las posibilidades a un razonablemente pequeño intervalo apelando a la teorema del valor intermedio). El método se suele converger, siempre que esta conjetura inicial es lo suficientemente cerca del cero desconocida, y que 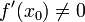. Además, para un cero de multiplicidad 1, la convergencia es al menos cuadrática (véase tasa de convergencia) en una vecindad del cero, lo que significa intuitivamente que el número de dígitos correctos aproximadamente al menos se duplica en cada paso. Más detalles se pueden encontrar en la sección de análisis a continuación.

Ejemplo

Considere el problema de encontrar el número positivo x con cos (x) = x ^3. Podemos reformular que como encontrar el cero de f (x) = cos (x) - x ^3. Hemos f '(x) = -sen (x) - 3 x ^2. Desde cos (x) ≤ 1 para todo x y x ^3> 1 para x> 1, sabemos que nuestra cero está comprendido entre 0 y 1. Intentamos un valor inicial de x ₀ = 0,5.

Los dígitos correctos están subrayados en el ejemplo anterior. En particular, x ₆ es correcto el número de decimales dados. Vemos que el número de dígitos decimales correctas después de los aumentos de punto de 2 (para x ₃₎ a 5 y 10, que ilustra la convergencia cuadrática.

Historia

El método de Newton fue descrito por Isaac Newton en De analysi por aequationes numero terminorum Infinitas (escrito en 1669, publicado en 1711 por William Jones) y en De metodis fluxionum et serierum infinitarum (escrito en 1671, traducido y publicado como Método de las fluxiones en 1736 por John Colson). Sin embargo, su descripción difiere sustancialmente de la descripción dada anteriormente moderna: Newton aplica el método sólo a polinomios. Él no calcula las aproximaciones sucesivas 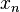, Pero calcula una secuencia de polinomios y sólo al final, llega a una aproximación de la raíz x. Por último, considera que el método de Newton como puramente algebraica y no se da cuenta de la conexión con el cálculo. Isaac Newton probablemente derivado su método de un método similar pero menos preciso por François Viète. La esencia del método de Viète se puede encontrar en la obra de la persa matemático Sharaf al-Din al-Tusi (Ypma 1995). Un caso especial del método de Newton para calcular raíces cuadradas se conocía mucho antes y, a menudo se le llama el Método babilónico.

El método de Newton fue publicado por primera vez en 1685 en el Tratado de Álgebra tanto histórica y práctica por John Wallis. En 1690, Joseph Raphson publicó una descripción simplificada en Universalis Análisis aequationum. Raphson otra vez visto el método de Newton puramente como un método algebraico y restringe su uso a polinomios, pero él se describe el método en términos de las aproximaciones sucesivas x _n en vez de la más complicada secuencia de polinomios utilizados por Newton. Por último, en 1740, Thomas Simpson describe el método de Newton como un método iterativo para resolver ecuaciones no lineales generales utilizando el cálculo fluxional, dando esencialmente la descripción anterior. En la misma publicación, Simpson también da la generalización a sistemas de dos ecuaciones y notas que el método de Newton se puede utilizar para resolver problemas de optimización configurando el gradiente a cero.

Arthur Cayley en 1879 en El problema imaginario Newton-Fourier fue el primero que se dio cuenta de las dificultades para generalizar el método de Newton a las raíces complejas de polinomios con grado mayor que 2 y complejos valores iniciales. Esto abrió el camino para el estudio de la teoría de iteraciones de funciones racionales.

Consideraciones prácticas

En general convergencia es cuadrática: el error se eleva al cuadrado esencialmente en cada paso (es decir, el número de dígitos exactos se duplica en cada paso). Hay algunas advertencias, sin embargo. En primer lugar, el método de Newton requiere que el derivado calcularse directamente. (Si el derivado se aproxima por la pendiente de una línea a través de dos puntos de la función, el Resultados método de la secante; esto puede ser más eficiente en función de cómo se mide el esfuerzo computacional.) En segundo lugar, si el valor inicial es demasiado lejos del cero real, el método de Newton puede fallar a converger. Debido a esto, las implementaciones más prácticas del método de Newton ponen un límite superior en el número de iteraciones y tal vez en el tamaño de las iteraciones. En tercer lugar, si el raíz que se busca tiene multiplicidad mayor que uno, la velocidad de convergencia es meramente lineales (reducción de errores por un factor constante en cada paso) a menos que se tomen medidas especiales.

Desde el más grave de los problemas anteriores es la posibilidad de un fallo de la convergencia, Press et al. (1992) presentan una versión del método de Newton que comienza en el punto medio de un intervalo en el que se conoce la raíz a mentir y se detiene la iteración si una iteración se genera que se encuentra fuera del intervalo.

Los desarrolladores de sistemas informáticos a gran escala que involucran búsqueda de raíces tienden a preferir el método de la secante sobre el método de Newton, porque el uso de un cociente de diferencias en lugar del derivado en el método de Newton implica que no es necesario que se mantenga el código adicional para calcular la derivada. En la práctica, las ventajas de mantener una base de código más pequeño por lo general superan las características de convergencia superiores del método de Newton.

Contraejemplos

Las líneas tangentes de x ^ 3 - 2 x + 2 en 0 y 1 de intersección del eje x en 1 y 0, respectivamente, que ilustran por qué el método de Newton oscila entre estos valores para algunos puntos de partida.

Punto de partida demasiado lejos

Si el punto de partida no está cerca de una raíz entonces convergencia puede dejar de ocurrir. Dejar

y tomar 0 como punto de partida. La primera iteración produce 1 y los segundos los rendimientos de iteración a 0 de modo que la secuencia de oscilará entre los dos sin converger a una raíz. En general, el comportamiento de la secuencia puede ser muy compleja. (Ver Fractal Newton.)

En los siguientes ejemplos, la raíz deseada está en cero por simplicidad-que podría haber sido colocado en otro lugar.

Derivado discontinua

Si el derivado no es continua en la raíz, entonces la convergencia puede dejar de ocurrir en cualquier barrio de la raíz. Considere la función

Entonces 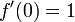y en otros lugares.

Dentro de cualquier barrio de la raíz, este derivado sigue cambiando signo cuando x tiende a 0 por la derecha (o la izquierda), mientras que 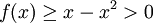para .

Así 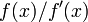está acotada cerca de la raíz y el método de Newton no converger, a pesar de que: la función es diferenciable en todas partes; el derivado no es cero en la raíz; es infinitamente diferenciable excepto en la raíz; y el derivado está delimitada en una zona de la raíz (a diferencia de su recíproco).

No segunda derivada

Si no hay una segunda derivada en la raíz, entonces la convergencia puede dejar de ser cuadrática. De hecho, y mucho

Entonces

Y

excepto cuando donde no está definido. Dado ,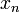

que tiene aproximadamente 4/3 veces más bits de precisión como 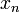tiene. Esto es menos de las 2 veces más que serían necesarios para la convergencia cuadrática. Así que la convergencia del método de Newton (en este caso) no es cuadrática, a pesar de que: la función es continuamente diferenciable en todas partes; el derivado no es cero en la raíz; y es infinitamente diferenciable excepto en la raíz deseada.

Cero derivado

Si la primera derivada es cero en la raíz, a continuación, la convergencia no será cuadrática. De hecho, y mucho

Entonces y consecuentemente . Así convergencia no es cuadrática, a pesar de que la función es infinitamente diferenciable en todas partes.

Análisis

Supongamos que la función f tiene un cero en α, es decir, f (α) = 0.

Si f es continuamente diferenciable y su derivada no se anula en α, entonces existe un barrio de α tal que para todos los valores de partida x ₀ en ese barrio, la secuencia {x _n} voluntad converger a α.

Si la función es continuamente diferenciable y su derivada no se anula en α y tiene una segunda derivada en α entonces la convergencia es cuadrática o más rápido. Si la segunda derivada no se anula en α entonces la convergencia es meramente cuadrática.

Si el derivado no desaparecer en α, entonces la convergencia es por lo general sólo lineal. En concreto, si f es dos veces continuamente diferenciable, y , Entonces existe un barrio de α tal que para todos los valores iniciales x ₀ en ese barrio, la secuencia de iteración converge linealmente, con registro de tasa ₁₀ 2 (Suli y Mayers, Ejercicio 1.6). Alternativamente, si y en otro lugar, en una entorno U de α, α ser un cero de r multiplicidad y si entonces existe un barrio de α tal que para todos los valores de partida x ₀ en ese barrio, la secuencia de iteración converge linealmente.

Sin embargo, incluso la convergencia lineal no está garantizada en situaciones patológicas.

En la práctica estos resultados son locales y la zona de convergencia no se conocen a priori, pero también hay algunos resultados sobre la convergencia global, por ejemplo, dado un barrio de la derecha de U ₊ α, si f es dos veces diferenciable en U ₊ y si , 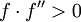en T _+, entonces, para cada x ₀ en U ₊ la secuencia x _k es monótonamente decreciente a α.

Las generalizaciones

Los sistemas no lineales de ecuaciones

Uno puede utilizar el método de Newton también para resolver los sistemas de ecuaciones k (no lineales), lo que equivale a encontrar los ceros de funciones continuamente diferenciables F: R → R ^{k k.} En la formulación dada anteriormente, uno entonces tiene que multiplicar la izquierda con la inversa de la k -by- k Jacobiano matriz J _F (x _n) en lugar de dividir por f '(x _n). En vez de computar realmente la inversa de esta matriz, se puede ahorrar tiempo resolviendo el sistema de ecuaciones lineales

por lo desconocido x _{n + 1} - x _n. Una vez más, este método sólo funciona si el valor inicial x ₀ es lo suficientemente cerca del cero real. Típicamente, una región que es comporta bien se encuentra primero con algún otro método y el método de Newton se utiliza entonces para "pulir" una raíz que ya se conoce aproximadamente.

Las ecuaciones no lineales en un espacio de Banach

Otra generalización es el método de Newton para encontrar un cero de una función f definida en una Espacio de Banach. En este caso la formulación es

,

donde 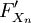es el Derivado Fréchet aplica en el punto . Uno necesita el derivado de Fréchet ser invertible en cada para que el método sea aplicable.

Funciones complejas

Cuencas de atracción para x ⁵ - 1 = 0; más oscuro significa más iteraciones para converger.

Cuando se trata de funciones complejas, sin embargo, el método de Newton se pueden aplicar directamente para encontrar sus ceros. Para muchas funciones complejas, el límite del conjunto (también conocido como el cuenca de atracción) de todos los valores de partida que hacen que el método converja a un cero en particular es un fractal .