
Transformada de Fourier discreta
Antecedentes de las escuelas de Wikipedia
SOS Children, que corre cerca de 200 sos escuelas en el mundo en desarrollo, organizó esta selección. Apadrina un niño para hacer una diferencia real.
| Transformadas de Fourier |
|---|
| Fourier continua transformar |
| Series de Fourier |
| Tiempo Transformada Discreta de Fourier |
| Transformada de Fourier discreta |
En matemáticas , la transformada discreta de Fourier (DFT) es una de las formas específicas de Análisis de Fourier. Como tal, se transforma una función a otra, que se llama el representación en el dominio de frecuencia, o simplemente la DFT, de la función original (que es a menudo una función en el dominio del tiempo). Sin embargo, la DFT requiere una función de entrada que es valores discretos y cuya no tienen un cero (finito) de duración limitada. Tales entradas son a menudo creadas por el muestreo de una función continua, como la voz de una persona. Y a diferencia de la de tiempo discreto transformada de Fourier (DTFT), sólo evalúa componentes de frecuencia suficientes para reconstruir el segmento finito que se analizó. Su transformada inversa no puede reproducir todo el dominio del tiempo, a menos que la entrada pasa a ser periódico (siempre). Por lo tanto, a menudo se dice que la DFT es una transformación para el análisis de Fourier de las funciones de tiempo discreto finito de dominio. Las funciones de base sinusoidales de la descomposición tienen las mismas propiedades.
Dado que la función de entrada es una secuencia finita de reales o números complejos , la DFT es ideal para procesamiento de la información almacenada en los ordenadores . En particular, la DFT se emplea extensamente en procesamiento de señales y campos relacionados para analizar las frecuencias de una muestreado señal, para resolver ecuaciones diferenciales parciales , y para realizar otras operaciones como circunvoluciones. La DFT se puede calcular de manera eficiente en la práctica el uso de un transformada rápida de Fourier (FFT) algoritmo.
Dado que los algoritmos FFT son tan comúnmente empleados para calcular la DFT, los dos términos se utilizan a menudo indistintamente en la configuración coloquiales, aunque hay una clara distinción: "DFT" se refiere a una transformación matemática, independientemente de cómo se calcula, mientras que "FFT" se refiere a uno cualquiera de varios algoritmos eficientes para la DFT. Esta distinción es aún más borrosa, sin embargo, por el sinónimo Fourier finita de transformación para la DFT, que aparentemente es anterior el término "transformada rápida de Fourier" (Cooley et al., 1969) pero tiene el mismo initialism.
Definición
La secuencia de n números complejos x 0, ..., x N -1 se transforma en la secuencia de n números complejos X 0, ..., X N -1 por el DFT de acuerdo con la fórmula:
donde  es un N-ésima primitiva raíz de la unidad.
es un N-ésima primitiva raíz de la unidad.
El transformar a veces se denota por el símbolo 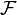 , Como en
, Como en  o
o  o
o  .
.
La transformada inversa de Fourier discreta (IDFT) viene dada por
Una simple descripción de estas ecuaciones es que los números complejos  representar la amplitud y fase de los diferentes componentes sinusoidales de la "señal" de entrada
representar la amplitud y fase de los diferentes componentes sinusoidales de la "señal" de entrada 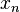 . La DFT calcula la
. La DFT calcula la  desde el
desde el 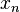 , Mientras que la IDFT muestra cómo calcular el
, Mientras que la IDFT muestra cómo calcular el 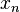 como una suma de componentes sinusoidales
como una suma de componentes sinusoidales  con frecuencia
con frecuencia  ciclos por muestra. Al escribir las ecuaciones de esta forma, estamos haciendo un amplio uso de La fórmula de Euler para expresar sinusoides en términos de exponenciales complejas, que son mucho más fáciles de manipular. (De la misma manera, por escrito
ciclos por muestra. Al escribir las ecuaciones de esta forma, estamos haciendo un amplio uso de La fórmula de Euler para expresar sinusoides en términos de exponenciales complejas, que son mucho más fáciles de manipular. (De la misma manera, por escrito  en forma polar , se obtiene inmediatamente la amplitud sinusoide de
en forma polar , se obtiene inmediatamente la amplitud sinusoide de  y la fase de la argumento complejo.) Una sutileza importante de esta representación, aliasing, se discute a continuación.
y la fase de la argumento complejo.) Una sutileza importante de esta representación, aliasing, se discute a continuación.
Tenga en cuenta que el factor de normalización multiplicando la DFT y IDFT (aquí 1 y 1 / N) y los signos de los exponentes no son más que convenciones, y difieren en algunos tratamientos. Los únicos requisitos de estas convenciones son que la DFT y IDFT tienen exponentes de distinto signo y que el producto de sus factores de normalización sean 1 / N. Una normalización de  tanto para la DFT y IDFT hace las transformaciones unitario, que tiene algunas ventajas teóricas, pero a menudo es más práctico en el cálculo numérico para llevar a cabo el escalado todos a la vez como anteriormente (y una escala unidad puede ser conveniente en otras formas).
tanto para la DFT y IDFT hace las transformaciones unitario, que tiene algunas ventajas teóricas, pero a menudo es más práctico en el cálculo numérico para llevar a cabo el escalado todos a la vez como anteriormente (y una escala unidad puede ser conveniente en otras formas).
(La convención de signo negativo en el exponente es a menudo conveniente porque significa que  es la amplitud de una "frecuencia positiva"
es la amplitud de una "frecuencia positiva"  . De manera equivalente, la DFT es a menudo considerado como un filtro adaptado: cuando se busca una frecuencia de 1, uno se correlaciona la señal de entrada con una frecuencia de -1).
. De manera equivalente, la DFT es a menudo considerado como un filtro adaptado: cuando se busca una frecuencia de 1, uno se correlaciona la señal de entrada con una frecuencia de -1).
En la siguiente discusión de los términos "secuencia" y "vector" serán considerados intercambiables.
Propiedades
Lo completo
La transformada discreta de Fourier es un invertible, transformación lineal
con  denota el conjunto de números complejos . En otras palabras, para cualquier n> 0, un vector dimensional N complejo tiene una DFT y una IDFT que son a su vez N -dimensional vectores complejos.
denota el conjunto de números complejos . En otras palabras, para cualquier n> 0, un vector dimensional N complejo tiene una DFT y una IDFT que son a su vez N -dimensional vectores complejos.
Ortogonalidad
Los vectores  para hombre base ortogonal sobre el conjunto de vectores complejos N -dimensional:
para hombre base ortogonal sobre el conjunto de vectores complejos N -dimensional:
donde  es el Delta Kronecker. Esta condición de ortogonalidad se puede utilizar para derivar la fórmula para la IDFT de la definición de la DFT, y es equivalente a la propiedad unitaridad a continuación.
es el Delta Kronecker. Esta condición de ortogonalidad se puede utilizar para derivar la fórmula para la IDFT de la definición de la DFT, y es equivalente a la propiedad unitaridad a continuación.
El teorema Plancherel y el teorema de Parseval
Si X e Y k k son las DFT de x n y y n respectivamente, entonces el Plancherel teorema:
donde la estrella denota conjugación compleja. El teorema de Parseval es un caso especial del teorema Plancherel y estados:
Estos teoremas son también equivalente a la condición unitaria a continuación.
Periodicidad
Si la expresión que define la DFT se evalúa para todos los números enteros  en lugar de sólo para
en lugar de sólo para  , Entonces la secuencia infinita resultante es una extensión periódica de la DFT, periódica con periodo N.
, Entonces la secuencia infinita resultante es una extensión periódica de la DFT, periódica con periodo N.
La periodicidad puede demostrarse directamente de la definición:
donde hemos utilizado el hecho de que  . De la misma manera se puede demostrar que la fórmula IDFT conduce a una extensión periódica.
. De la misma manera se puede demostrar que la fórmula IDFT conduce a una extensión periódica.
El teorema de cambio
Multiplicando 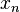 por una fase lineal
por una fase lineal  para algún entero
para algún entero  corresponde a un desplazamiento circular de la salida
corresponde a un desplazamiento circular de la salida  :
:  se sustituye por
se sustituye por  , Donde se interpreta el subíndice de módulo
, Donde se interpreta el subíndice de módulo  (Es decir, periódicamente). Del mismo modo, un desplazamiento circular de la entrada
(Es decir, periódicamente). Del mismo modo, un desplazamiento circular de la entrada 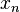 corresponde a la multiplicación de la salida
corresponde a la multiplicación de la salida  por una fase lineal. Matemáticamente, si
por una fase lineal. Matemáticamente, si  representa el vector x entonces
representa el vector x entonces
- si

- entonces

- y

Teorema de convolución circular y el teorema de correlación cruzada
La teorema de convolución para el tiempo continuo y discreto de Fourier transforma indica que una convolución de dos secuencias infinitas se puede obtener como la transformada inversa del producto de las transformadas individuales. Con secuencias y transformadas de longitud N, A surge la circularidad:
La cantidad entre paréntesis es 0 para todos los valores de  excepto las de la forma
excepto las de la forma  , Donde
, Donde  es cualquier número entero. En esos valores, es 1. Por lo tanto, puede ser reemplazada por una suma infinita de Funciones delta Kronecker, y seguimos en consecuencia. Tenga en cuenta que también podemos extender los límites de
es cualquier número entero. En esos valores, es 1. Por lo tanto, puede ser reemplazada por una suma infinita de Funciones delta Kronecker, y seguimos en consecuencia. Tenga en cuenta que también podemos extender los límites de  hasta el infinito, con el entendimiento de que la
hasta el infinito, con el entendimiento de que la  y
y  secuencias se definen como 0 fuera de [0, N-1]:
secuencias se definen como 0 fuera de [0, N-1]:
que es la convolución de la  secuencia con un renovado periódicamente
secuencia con un renovado periódicamente  secuencia definida por:
secuencia definida por:
Del mismo modo, se puede demostrar que:
cuál es el correlación cruzada de  y
y 
Una evaluación directa de la convolución o correlación suma, más arriba, requiere  operaciones. Un método indirecto, usando transformaciones, puede aprovechar la
operaciones. Un método indirecto, usando transformaciones, puede aprovechar la  eficiencia de la transformada rápida de Fourier (FFT) para lograr un rendimiento mucho mejor. Además, circunvoluciones pueden utilizarse para calcular de manera eficiente a través de DFT Algoritmo FFT de Rader y Algoritmo FFT de Bluestein.
eficiencia de la transformada rápida de Fourier (FFT) para lograr un rendimiento mucho mejor. Además, circunvoluciones pueden utilizarse para calcular de manera eficiente a través de DFT Algoritmo FFT de Rader y Algoritmo FFT de Bluestein.
Los métodos también han sido desarrollados para utilizar la convolución circular como parte de un proceso eficiente que logra normal (no circular) convolución con una  o
o  secuencia potencialmente mucho más largo que el tamaño práctico transformar (N). Dos de tales métodos se denominan solapar-guardar y superponerse a agregar.
secuencia potencialmente mucho más largo que el tamaño práctico transformar (N). Dos de tales métodos se denominan solapar-guardar y superponerse a agregar.
Polinomio de interpolación trigonométrica
La polinomio de interpolación trigonométrica
 para
para  incluso,
incluso,  para
para  impar,
impar,
donde los coeficientes X k / N son dados por el DFT de x n anterior, satisface la propiedad de interpolación  para
para  .
.
Porque aun  , Observe que la Componente Nyquist
, Observe que la Componente Nyquist  se maneja de forma especial.
se maneja de forma especial.
Esta interpolación no es única: aliasing implica que se podría añadir N a cualquiera de las frecuencias complejo de sinusoides (por ejemplo, cambiando  a
a  ) Sin cambiar la propiedad de interpolación, pero dando valores diferentes en entre el
) Sin cambiar la propiedad de interpolación, pero dando valores diferentes en entre el 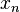 puntos. La elección anteriormente, sin embargo, es típico porque tiene dos propiedades útiles. En primer lugar, se compone de sinusoides cuyas frecuencias tener las magnitudes más pequeñas posibles, y por lo tanto minimiza la media cuadrática pendiente
puntos. La elección anteriormente, sin embargo, es típico porque tiene dos propiedades útiles. En primer lugar, se compone de sinusoides cuyas frecuencias tener las magnitudes más pequeñas posibles, y por lo tanto minimiza la media cuadrática pendiente  de la función de interpolación. En segundo lugar, si el
de la función de interpolación. En segundo lugar, si el 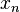 son números reales, entonces
son números reales, entonces  es real también.
es real también.
En contraste, la más obvia polinomio de interpolación trigonométrica es aquel en el que las frecuencias van de 0 a  (En lugar de más o menos
(En lugar de más o menos  a
a  como anteriormente), similar a la fórmula DFT inversa. Esta interpolación no minimiza la pendiente, y no es por lo general un valor real de los bienes
como anteriormente), similar a la fórmula DFT inversa. Esta interpolación no minimiza la pendiente, y no es por lo general un valor real de los bienes 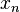 ; su uso es un error común.
; su uso es un error común.
El unitario DFT
Otra manera de mirar el DFT es observar que en la discusión anterior, la DFT se puede expresar como una Matriz Vandermonde:
donde
es una primitiva Raíz enésima de la unidad. La transformada inversa viene dada por la inversa de la matriz anterior:
Con constantes de normalización unitarias  , La DFT se convierte en una transformación unitaria, definida por una matriz unitaria:
, La DFT se convierte en una transformación unitaria, definida por una matriz unitaria:
donde det () es el determinante función. El determinante es el producto de los valores propios, que son siempre  o
o  como se describe abajo. En un espacio vectorial real, una transformación unitaria puede ser considerado simplemente como una rotación rígida del sistema de coordenadas, y todas las propiedades de una rotación rígida se puede encontrar en el unitaria DFT.
como se describe abajo. En un espacio vectorial real, una transformación unitaria puede ser considerado simplemente como una rotación rígida del sistema de coordenadas, y todas las propiedades de una rotación rígida se puede encontrar en el unitaria DFT.
La ortogonalidad de la DFT se expresa ahora como una condición ortonormalidad (que surge en muchas áreas de las matemáticas como se describe en raíz de la unidad):
Si  se define como la DFT unitaria del vector
se define como la DFT unitaria del vector  entonces
entonces
y la Plancherel teorema se expresa como:
Si vemos la DFT como una simple transformación que simplemente especifica las componentes de un vector en un nuevo sistema de coordenadas de coordenadas, entonces lo anterior es sólo la afirmación de que el producto escalar de dos vectores se conserva bajo una transformación DFT unitario. Para el caso especial  , Esto implica que la longitud de un vector se conserva como bien esto es sólo El teorema de Parseval:
, Esto implica que la longitud de un vector se conserva como bien esto es sólo El teorema de Parseval:
Expresando la DFT inversa en términos de la DFT
Una propiedad útil de la DFT es que la DFT inversa se puede expresar fácilmente en términos de la (adelante) DFT, a través de varios "trucos" muy conocidos. (Por ejemplo, en los cálculos, a menudo es conveniente sólo implementar una transformada rápida de Fourier correspondiente a una transformación dirección y luego para obtener la otra dirección de la transformación de la primera).
En primer lugar, podemos calcular la DFT inversa mediante la inversión de las entradas:
(Como de costumbre, los subíndices se interpretan módulo  ; Así, por
; Así, por  , Tenemos
, Tenemos  .)
.)
En segundo lugar, también se puede conjugar las entradas y salidas:
En tercer lugar, una variante de este truco conjugación, que a veces es preferible, ya que no requiere ninguna modificación de los valores de los datos, implica el intercambio de partes reales e imaginarias (que se pueden hacer en un ordenador simplemente modificando punteros). Definir swap ( 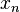 ) Como
) Como 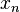 con sus partes real e imaginaria intercambiados, es decir, si
con sus partes real e imaginaria intercambiados, es decir, si  luego cambiar (
luego cambiar ( 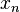 ) Es
) Es  . De manera equivalente, de intercambio (
. De manera equivalente, de intercambio ( 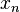 ) Es igual
) Es igual  . Entonces
. Entonces
Es decir, la transformada inversa es la misma que la transformada directa con las partes real e imaginaria intercambian tanto para la entrada y la salida, hasta una normalización (Duhamel et al., 1988).
El truco conjugación también se puede utilizar para definir una transformación nueva, estrechamente relacionada con la DFT, es decir involutary, es decir, que es su propio inverso. En particular,  es claramente su propio inverso:
es claramente su propio inverso:  . Una transformación involutary estrechamente relacionados (por un factor de (1 + i) / √2) es
. Una transformación involutary estrechamente relacionados (por un factor de (1 + i) / √2) es  , Ya que la
, Ya que la  factores en
factores en  cancelar el 2. Para las entradas reales
cancelar el 2. Para las entradas reales  , La parte real de
, La parte real de  no es otro que el discreta Hartley transformada, que también es involutary.
no es otro que el discreta Hartley transformada, que también es involutary.
Valores propios y vectores propios
Los valores propios de la matriz DFT son simples y bien conocido, mientras que los vectores propios son complicados, no es único, y son objeto de una investigación en curso.
Considere la forma unitaria  definido anteriormente para la DFT de longitud
definido anteriormente para la DFT de longitud  , Donde
, Donde  . Esta matriz satisface la ecuación:
. Esta matriz satisface la ecuación:
Esto se puede ver a partir de las propiedades inversas anteriores: operativo  dos veces da los datos originales en el orden inverso, de modo operativo
dos veces da los datos originales en el orden inverso, de modo operativo  cuatro veces te devuelven los datos originales y es por lo tanto la matriz de identidad. Esto significa que los valores propios
cuatro veces te devuelven los datos originales y es por lo tanto la matriz de identidad. Esto significa que los valores propios 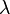 satisfacer una ecuación característica:
satisfacer una ecuación característica:
Por lo tanto, los valores propios de  son la cuarta raíces de la unidad:
son la cuarta raíces de la unidad: 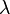 es 1, -1, + i, o - i.
es 1, -1, + i, o - i.
Dado que sólo hay cuatro valores propios distintos de este  matriz, que tienen algún multiplicidad . La multiplicidad da el número de vectores propios linealmente independientes correspondientes a cada valor propio. (Tenga en cuenta que hay N vectores propios independientes; una matriz unitaria nunca es defectuoso.)
matriz, que tienen algún multiplicidad . La multiplicidad da el número de vectores propios linealmente independientes correspondientes a cada valor propio. (Tenga en cuenta que hay N vectores propios independientes; una matriz unitaria nunca es defectuoso.)
El problema de su multiplicidad fue resuelto por McClellan y Parks (1972), aunque posteriormente se ha demostrado haber sido equivalente a un problema resuelto por Gauss (Dickinson y Steiglitz, 1982). La multiplicidad depende del valor de  modulo 4, y está dada por la siguiente tabla:
modulo 4, y está dada por la siguiente tabla:
| N tamaño | λ = 1 | λ = -1 | λ = - i | λ = + i |
|---|---|---|---|---|
| 4 m | m + 1 | m | m | m - 1 |
| 4 m + 1 | m + 1 | m | m | m |
| 4 m + 2 | m + 1 | m + 1 | m | m |
| 4 m + 3 | m + 1 | m + 1 | m + 1 | m |
Desafortunadamente, no se conoce ninguna fórmula analítica simple para los vectores propios. Además, los vectores propios no son únicos, ya que cualquier combinación lineal de vectores propios para el mismo valor propio es también un vector propio para ese valor propio. Varios investigadores han propuesto diferentes opciones de vectores propios, seleccionados para satisfacer propiedades útiles como ortogonalidad y tener formas "simples" (por ejemplo, McClellan y Parques, 1972; Dickinson y Steiglitz, 1982; Grünbaum, 1982; Atakishiyev y Wolf, 1997;. Candan et al, 2000; Hanna et al., 2004).
La elección de los vectores propios de la matriz DFT se ha convertido en importante en los últimos años con el fin de definir un análogo discreto de la Fourier fraccional transformar-la matriz DFT se puede tomar a potencias fraccionarias exponenciando los valores propios (por ejemplo, Rubio y Santhanam, 2005). Para el continua transformada de Fourier, las funciones propias ortogonales naturales son la Funciones de Hermite, así diversos análogos discretos de éstos se han empleado como los vectores propios de la DFT, tales como la Polinomios Kravchuk (Atakishiyev y Wolf, 1997). El "mejor" opción de vectores propios para definir una discreta de Fourier fraccionaria transformar sigue siendo una pregunta abierta, sin embargo.
La DFT-real de entrada
Si  son números reales , ya que a menudo se encuentran en las aplicaciones prácticas, entonces la DFT obedece a la simetría:
son números reales , ya que a menudo se encuentran en las aplicaciones prácticas, entonces la DFT obedece a la simetría:
donde la estrella denota conjugación compleja y los subíndices se interpretan módulo N.
Por lo tanto, la salida de DFT para las entradas reales es un medio redundante, y se obtiene la información completa con sólo mirar aproximadamente la mitad de las salidas  . En este caso, el elemento "DC"
. En este caso, el elemento "DC"  es puramente real, y para incluso n el elemento "Nyquist"
es puramente real, y para incluso n el elemento "Nyquist"  También es real, por lo que hay exactamente N no redundantes números reales en el primer semestre + elemento de Nyquist del complejo de salida X.
También es real, por lo que hay exactamente N no redundantes números reales en el primer semestre + elemento de Nyquist del complejo de salida X.
Uso La fórmula de Euler, el polinomio de interpolación trigonométrica a continuación puede ser interpretada como una suma de funciones seno y coseno.
Generalizada / desplazado DFT
Es posible desplazar el muestreo transformar en el tiempo y / o dominio de la frecuencia por algunos cambios reales a y b, respectivamente. Esto a veces se conoce como una DFT generalizada (o GDFT), también llamado el desplazado DFT o compensar DFT, y tiene propiedades análogas a la DFT ordinaria:
Muy a menudo, los cambios de  (La mitad de una muestra) se utilizan. Mientras que la DFT ordinaria corresponde a una señal periódica en el tiempo y dominio de la frecuencia,
(La mitad de una muestra) se utilizan. Mientras que la DFT ordinaria corresponde a una señal periódica en el tiempo y dominio de la frecuencia,  produce una señal que es anti-periódica en el dominio de la frecuencia (
produce una señal que es anti-periódica en el dominio de la frecuencia (  ) Y viceversa para
) Y viceversa para  . Por lo tanto, el caso específico de
. Por lo tanto, el caso específico de  se conoce como un número impar de la frecuencia de Fourier en tiempo impar transformada discreta (DFT o O 2). Tal desplazado transformaciones se utilizan con mayor frecuencia para los datos simétricos, para representar diferentes simetrías de frontera, y para los datos-real simétrica que corresponden a las diferentes formas de la discreta coseno y transformadas seno.
se conoce como un número impar de la frecuencia de Fourier en tiempo impar transformada discreta (DFT o O 2). Tal desplazado transformaciones se utilizan con mayor frecuencia para los datos simétricos, para representar diferentes simetrías de frontera, y para los datos-real simétrica que corresponden a las diferentes formas de la discreta coseno y transformadas seno.
Otra opción interesante es  , Que se llama la DFT centrada (o CDFT). La DFT centrado tiene la propiedad útil que, cuando
, Que se llama la DFT centrada (o CDFT). La DFT centrado tiene la propiedad útil que, cuando  es un múltiplo de cuatro, los cuatro de sus valores propios (ver arriba) tienen multiplicidades iguales (Rubio y Santhanam, 2005).
es un múltiplo de cuatro, los cuatro de sus valores propios (ver arriba) tienen multiplicidades iguales (Rubio y Santhanam, 2005).
La transformada discreta de Fourier se puede ver como un caso especial de la transformada z, evaluado en el círculo unidad en el plano complejo; más transformadas z generales corresponden a los cambios complejos a y b anterior.
Multidimensional DFT
La DFT ordinaria calcula la transformada de un conjunto de datos "unidimensional": una secuencia (o array) 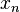 que es una función de una variable discreta
que es una función de una variable discreta  . Más generalmente, se puede definir la DFT multidimensional de una matriz multidimensional
. Más generalmente, se puede definir la DFT multidimensional de una matriz multidimensional  que es una función de
que es una función de  variables discretas
variables discretas  para
para  en
en  :
:
donde  como anteriormente y la
como anteriormente y la  índices del producto van desde
índices del producto van desde  . Esto se expresa de forma más compacta en notación vectorial, donde definimos
. Esto se expresa de forma más compacta en notación vectorial, donde definimos  y
y  como
como  vectores dimensionales de los índices de 0 a
vectores dimensionales de los índices de 0 a  , Que definimos como
, Que definimos como  :
:
donde la división  se define como
se define como  a realizar elemento a elemento, y la suma denota el conjunto de sumas anidados anteriores.
a realizar elemento a elemento, y la suma denota el conjunto de sumas anidados anteriores.
La inversa de la DFT multi-dimensional es, de forma análoga al caso unidimensional, dada por:
El multidimensional DFT tiene una interpretación sencilla. Así como el DFT unidimensional expresa la entrada 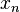 como una superposición de sinusoides, la multidimensional DFT expresa la entrada como una superposición de ondas planas o sinusoides oscilantes largo de la dirección
como una superposición de sinusoides, la multidimensional DFT expresa la entrada como una superposición de ondas planas o sinusoides oscilantes largo de la dirección  en el espacio y tiene una amplitud
en el espacio y tiene una amplitud  . Tal descomposición es de gran importancia para todo, desde procesamiento digital de la imagen (d = 2) a la solución de ecuaciones diferenciales parciales en tres dimensiones (d = 3) rompiendo la solución arriba en ondas planas.
. Tal descomposición es de gran importancia para todo, desde procesamiento digital de la imagen (d = 2) a la solución de ecuaciones diferenciales parciales en tres dimensiones (d = 3) rompiendo la solución arriba en ondas planas.
Computacionalmente, el multidimensional DFT es simplemente la composición de una secuencia de DFT de una dimensión a lo largo de cada dimensión. Por ejemplo, en el caso de dos dimensiones  uno primero puede calcular la
uno primero puede calcular la  DFT independientes de las filas (es decir, a lo largo
DFT independientes de las filas (es decir, a lo largo  ) Para formar una nueva matriz
) Para formar una nueva matriz  , Y luego calcular la
, Y luego calcular la  DFT independientes de
DFT independientes de  a lo largo de las columnas (junto
a lo largo de las columnas (junto  ) Para formar el resultado final
) Para formar el resultado final  . O bien, se puede transformar las columnas y luego las filas: el orden es irrelevante porque las sumas anidados anterior viaje .
. O bien, se puede transformar las columnas y luego las filas: el orden es irrelevante porque las sumas anidados anterior viaje .
Debido a esto, dado una manera de calcular una DFT de una dimensión (por ejemplo, un algoritmo FFT unidimensional ordinario), uno tiene inmediatamente una forma de calcular de manera eficiente el multidimensional DFT. Esto se conoce como un algoritmo de fila-columna, aunque también son intrínsecamente algoritmos FFT multidimensional.
La entrada de bienes multidimensional DFT
Si las entradas  son números reales , ya que a menudo están en las aplicaciones prácticas, a continuación, las salidas DFT tienen una simetría conjugado similar al caso unidimensional arriba:
son números reales , ya que a menudo están en las aplicaciones prácticas, a continuación, las salidas DFT tienen una simetría conjugado similar al caso unidimensional arriba:
donde la estrella denota conjugación compleja y la  subíndice-ésimo se interpreta módulo
subíndice-ésimo se interpreta módulo  (Por
(Por  ).
).
Aplicaciones
La DFT ha visto el uso de ancho a través de un gran número de campos; que sólo esbozamos algunos ejemplos a continuación (ver también las referencias al final). Todas las aplicaciones de la DFT dependen crucialmente de la disponibilidad de un algoritmo rápido para calcular transformadas de Fourier discreta y sus inversas, una transformada rápida de Fourier.
El análisis espectral
Cuando la DFT se utiliza para el análisis espectral, la  secuencia por lo general representa un conjunto finito de uniformemente espaciados de tiempo muestras de algunos de señal
secuencia por lo general representa un conjunto finito de uniformemente espaciados de tiempo muestras de algunos de señal  , Donde t representa el tiempo. La conversión de tiempo continuo de muestras (de tiempo discreto) cambia el subyacente Transformada de Fourier de x (t) en una Fourier de tiempo discreto de transformación (DTFT), que conlleva generalmente un tipo de distorsión llamada aliasing. La elección de una frecuencia de muestreo adecuado (vea Frecuencia de Nyquist) es la clave para minimizar la distorsión. Del mismo modo, la conversión de un tiempo muy largo (o infinito) secuencia a un tamaño manejable implica un tipo de distorsión llamada fugas, que se manifiesta como una pérdida de detalle (resolución aka) en el DTFT. Elección de una longitud de sub-secuencia apropiada es la clave principal para minimizar ese efecto. Cuando los datos disponibles (y tiempo para procesarlo) es más que la cantidad necesaria para alcanzar la resolución de frecuencia deseada, una técnica estándar es de realizar múltiples DFT, por ejemplo, para crear un espectrograma. Si el resultado deseado es un espectro de potencia y ruido o aleatoriedad está presente en los datos, el promedio de las componentes de magnitud de las múltiples DFT es un procedimiento útil para reducir la varianza del espectro (también llamado periodograma en este contexto); Dos ejemplos de tales técnicas son la Método de Welch y la Método de Bartlett.
, Donde t representa el tiempo. La conversión de tiempo continuo de muestras (de tiempo discreto) cambia el subyacente Transformada de Fourier de x (t) en una Fourier de tiempo discreto de transformación (DTFT), que conlleva generalmente un tipo de distorsión llamada aliasing. La elección de una frecuencia de muestreo adecuado (vea Frecuencia de Nyquist) es la clave para minimizar la distorsión. Del mismo modo, la conversión de un tiempo muy largo (o infinito) secuencia a un tamaño manejable implica un tipo de distorsión llamada fugas, que se manifiesta como una pérdida de detalle (resolución aka) en el DTFT. Elección de una longitud de sub-secuencia apropiada es la clave principal para minimizar ese efecto. Cuando los datos disponibles (y tiempo para procesarlo) es más que la cantidad necesaria para alcanzar la resolución de frecuencia deseada, una técnica estándar es de realizar múltiples DFT, por ejemplo, para crear un espectrograma. Si el resultado deseado es un espectro de potencia y ruido o aleatoriedad está presente en los datos, el promedio de las componentes de magnitud de las múltiples DFT es un procedimiento útil para reducir la varianza del espectro (también llamado periodograma en este contexto); Dos ejemplos de tales técnicas son la Método de Welch y la Método de Bartlett.
Una fuente final de distorsión (o quizás ilusión) es el propio DFT, porque es sólo una muestra discreta de la DTFT, que es una función de un dominio de frecuencia continua. Eso puede ser mitigado por el aumento de la resolución de la DFT. Este procedimiento se ilustra en el de tiempo discreto transformada de Fourier artículo.
- El procedimiento se refiere a veces como padding-cero, que es una implementación particular usado en conjunción con el transformada rápida de Fourier (FFT) algoritmo. La ineficiencia de realizar multiplicaciones y sumas con cero valorado "muestras" es más que compensado por la eficiencia inherente de la FFT.
- Como ya se ha señalado, las fugas impone un límite a la resolución inherente de la DTFT. Así que hay un límite práctico para el beneficio que se puede obtener a partir de una DFT de grano fino.
Compresión de datos
El campo de procesamiento de señal digital depende en gran medida las operaciones en el dominio de la frecuencia (es decir, la transformada de Fourier). Por ejemplo, varios imágenes con pérdidas y los métodos de compresión de sonido emplean la transformada de Fourier discreta: la señal se corta en segmentos cortos, cada uno se transforma, y luego los coeficientes de Fourier de altas frecuencias, que se supone que son imperceptibles, se descartan. El descompresor calcula la transformada inversa basada en este reducido número de coeficientes de Fourier. (Aplicaciones de compresión a menudo usan una forma especializada de la DFT, la transformada de coseno discreta o, a veces la coseno discreta modificada transformar.)
Ecuaciones diferenciales parciales
Transformadas de Fourier discretas se utilizan a menudo para resolver ecuaciones diferenciales parciales , donde de nuevo la DFT se utiliza como una aproximación para el Serie de Fourier (que se recupera en el límite de infinito N). La ventaja de este enfoque es que se expande la señal en exponenciales complejas e inx, que son funciones propias de diferenciación: d / dx = e inx en e inx. Por lo tanto, en la representación de Fourier, la diferenciación es simple-vamos a multiplicarlo por en. Una ecuación diferencial lineal con coeficientes constantes se transforma en una ecuación algebraica fácilmente solucionable. Una vez, utiliza la DFT inversa para transformar el resultado en la representación espacial ordinaria. Este enfoque se denomina método espectral.
Multiplicación de polinomios
Supongamos que queremos calcular el producto c polinomio (x) = a (x) · b (x). La expresión producto ordinario para los coeficientes de c implica un lineal (acíclico) de convolución, donde los índices no "se envuelven alrededor." Esto puede ser reescrita como una convolución cíclica mediante la adopción de los vectores de coeficientes de a (x) yb (x) con término constante primero, a continuación, añadiendo ceros manera que el coeficiente resultante vectores A y B tienen dimensión d> deg (a (x) ) + deg (b (x)). Luego,
Donde c es el vector de coeficientes para c (x), y el operador de convolución  se define de manera
se define de manera
Pero convolución se convierte en la multiplicación bajo la DFT:
Aquí el producto vectorial se toma elementwise. Así, los coeficientes del polinomio producto c (x) son sólo los términos 0, ..., deg (a (x)) + deg (b (x)) del vector de coeficiente
Con un Fast transformada de Fourier, el algoritmo resultante toma O (N log N) operaciones aritméticas. Debido a su simplicidad y velocidad, el Cooley-Tukey FFT algoritmo, que se limita a tamaños compuestos, a menudo se elige para la operación de transformación. En este caso, d debe ser elegido como el menor entero mayor que la suma de los grados de polinomio de entrada que es factorizable en pequeños factores primos (por ejemplo, 2, 3, y 5, dependiendo de la implementación FFT).
La multiplicación de enteros grandes
El más rápido conocido algoritmos para la multiplicación de muy grandes números enteros utilizan el método de multiplicación de polinomios descrito anteriormente. Los enteros pueden ser tratadas como el valor de un polinomio evaluado específicamente en la base número, con los coeficientes del polinomio correspondiente a los dígitos en esa base. Después de multiplicación de polinomios, un paso equipaje de propagación relativamente baja complejidad completa la multiplicación.
Algunos transformada de Fourier discreta pares
 |  | Nota |
|---|---|---|
 |  | Teorema del desfase |
 |  | |
 |  | Bienes DFT |
 |  | |
 |  |
Derivación como series de Fourier
La DFT se puede derivar como un truncamiento de la Serie de Fourier de una secuencia periódica de impulsos.
DFT sobre campos distintos de los números complejos
Muchas de las propiedades de la DFT depende únicamente del hecho de que  es un raíz primitiva de la unidad, a veces denotada
es un raíz primitiva de la unidad, a veces denotada  o
o  (De modo que
(De modo que  ). Tales propiedades incluyen la integridad, la ortogonalidad, Plancherel / Parseval, la periodicidad, cambio, de convolución, y las propiedades de unitariedad anteriormente, así como muchos algoritmos FFT. Por esta razón, la Transformada Discreta de Fourier se puede definir mediante el uso de raíces de la unidad en ámbitos distintos de los números complejos; Para obtener más información, consulte transformada de Fourier discreta (general).
). Tales propiedades incluyen la integridad, la ortogonalidad, Plancherel / Parseval, la periodicidad, cambio, de convolución, y las propiedades de unitariedad anteriormente, así como muchos algoritmos FFT. Por esta razón, la Transformada Discreta de Fourier se puede definir mediante el uso de raíces de la unidad en ámbitos distintos de los números complejos; Para obtener más información, consulte transformada de Fourier discreta (general).




































