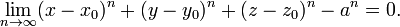Cubo
Antecedentes de las escuelas de Wikipedia
SOS Children, que corre cerca de 200 sos escuelas en el mundo en desarrollo, organizó esta selección. Infantil SOS es la mayor donación de caridad del mundo niños huérfanos y abandonados de la oportunidad de la vida familiar.
| Hexahedron Regular | |
|---|---|
 (Haga clic aquí para el modelo de rotación) | |
| Tipo | Sólidos platónicos |
| Elementos | F = 6, E = 12 V = 8 (χ = 2) |
| Las caras de los lados | 6 {4} |
| Símbolo de Schläfli | {4,3} |
| Símbolo Wythoff | 3 | 2 4 |
| Diagrama Coxeter | |
| Simetría | O h, BC 3, [4,3], (* 432) |
| Grupo de rotación | O, [4,3] +, (432) |
| Referencias | U 06, C 18, W 3 |
| Propiedades | Regular convexo zonohedron |
| Ángulo diedro | 90 ° |
 4.4.4 ( Vertex figura) |  Octaedro ( poliedro dual) |
 Neto | |
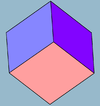
En geometría , un cubo es una objeto sólido tridimensional delimitado por seis cuadrados caras, facetas o caras, con tres reuniones en cada vértice. El cubo también puede ser llamado un regular hexaedro y es uno de los cinco sólidos platónicos . Es un tipo especial de plaza prisma de sección rectangular paralelepípedo y de trapezoedro trigonal. El cubo es dual a la octaedro . Se tiene simetría cúbica (también llamado simetría octaédrica). Es especial por ser una cuboide y una romboedro.
Proyecciones ortogonales
El cubo tiene cuatro especiales proyecciones ortogonales, centradas, en un vértice, bordes, la cara y normales para su figura de la cima. El primero y tercero corresponden a la A y 2 B 2 Aviones de Coxeter.
| Centrado por | Cara | Vértice |
|---|---|---|
| Aviones de Coxeter | B 2  | A 2  |
| Descriptivo simetría | ||
| Vistas inclinadas |  |  |
Coordenadas cartesianas
Para un cubo centrado en el origen, con los bordes paralelos a los ejes y con una longitud de borde de 2, las coordenadas cartesianas de los vértices son
- (± 1, ± 1, ± 1)
mientras que el interior se compone de todos los puntos (x 0, x 1, x 2) con -1 <x i <1.
Ecuación en R3
En la geometría analítica , la superficie de un cubo con centro (x 0, y 0, z 0) y longitud de la arista de 2a es la locus de todos los puntos (x, y, z) tal que
Fórmulas
Para un cubo de longitud de arista  ,
,
| área de superficie | 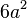 |
| volumen |  |
| enfrentar diagonal |  |
| espacio diagonal |  |
| radio de esfera circunscrita |  |
| radio de la esfera tangente a los bordes | 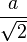 |
| radio de esfera inscrita |  |
| ángulos entre las caras (en radianes ) | 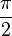 |
Como el volumen de un cubo es la tercera potencia de sus lados  , terceras potencias se llaman cubos, por analogía con plazas y segunda poderes.
, terceras potencias se llaman cubos, por analogía con plazas y segunda poderes.
Un cubo tiene el mayor volumen entre cuboides (cajas rectangulares) con un determinado área de superficie. Además, un cubo tiene el mayor volumen entre cuboides con el mismo tamaño total lineal (largo + ancho + altura).
Colorantes uniformes y simetría
El cubo tiene tres coloraciones uniformes, nombrados por los colores de las caras cuadradas alrededor de cada vértice: 111, 112, 123.
El cubo tiene tres clases de simetría, que pueden estar representados por vértice-transitivo colorear las caras. La más alta simetría octaédrica O h tiene todas las caras del mismo color. La diedro 4h simetría D proviene del cubo de ser un prisma, con los cuatro lados ser el mismo color. El 2h más bajo simetría D es también una simetría prismática, con colores alternando los lados, por lo que hay tres colores, emparejados por lados opuestos. Cada forma tiene una simetría diferente Símbolo Wythoff.
Las relaciones geométricas

Un cubo tiene once redes (que se muestra arriba): es decir, hay maneras de once para aplanar un cubo hueco cortando siete bordes. Para colorear el cubo para que no hay dos caras adyacentes tienen el mismo color, se necesitaría al menos tres colores.
El cubo es la célula de el único mosaico regular de espacio euclidiano tridimensional. También es único entre los sólidos platónicos en que tiene caras con un número par de lados y, por consiguiente, es el único miembro de dicho grupo que es una zonohedron (cada rostro tiene un punto de simetría).
El cubo se puede cortar en seis idéntica pirámides cuadradas. Si estas pirámides cuadradas se unen entonces a las caras de un segundo cubo, una se obtiene dodecaedro rómbico (con pares de triángulos coplanares combinados en caras rómbicas.)
Otras dimensiones
El análogo de un cubo de cuatro dimensiones espacio euclidiano tiene un nombre especial-un tesseract o hipercubo. Más bien, un hipercubo (o n cubo dimensional o simplemente n -cube) es el análogo del cubo en el espacio euclidiano n-dimensional y un tesseract es el orden-4 hipercubo. Un hipercubo también se denomina politopo medida.
Hay análogos del cubo en dimensiones más bajas también: una punto en dimensión 0, un segmento en una dimensión y un cuadrado en dos dimensiones.
Poliedros Relacionados

El cociente del cubo por el mapa antípoda produce una poliedro proyectiva, la hemicubo.
Si el cubo original tiene longitud de borde 1, su poliedro dual (un octaedro ) tiene una longitud de borde  .
.
El cubo es un caso especial en diversas clases de poliedros en general:
| Nombre | Igualdad borde del largo? | Ángulos iguales? | Ángulos rectos? |
|---|---|---|---|
| Cubo | Sí | Sí | Sí |
| Romboedro | Sí | Sí | No |
| Cuboides | No | Sí | Sí |
| Paralelepípedo | No | Sí | No |
| cuadrilátero enfrentado hexaedro | No | No | No |
Los vértices de un cubo se pueden agrupar en dos grupos de cuatro, formando cada uno un habitual tetraedro ; más generalmente esto se conoce como una demicube. Estos dos juntos forman un habitual compuesto, la stella octangula. La intersección de las dos formas de un octaedro regular. Las simetrías de un tetraedro regular corresponden a las de un cubo que asignar cada tetraedro a sí mismo; las otras simetrías del cubo mapa los dos entre sí.
Uno de tales tetraedro regular tiene un volumen de 1/2 de la del cubo. El espacio restante se compone de cuatro tetraedros igual irregular con un volumen de 1/6 de la del cubo, cada uno.
La cubo rectificada es el cuboctaedro. Si rincones más pequeños se cortan obtenemos un poliedro de seis caras octogonales y ocho triangulares. En particular, podemos obtener octógonos regulares ( cubo truncado). La rhombicuboctahedron se obtiene cortando ambas esquinas y bordes para la cantidad correcta.
Un cubo puede ser inscrito en un dodecaedro de modo que cada vértice del cubo es un vértice del dodecaedro y cada borde es una diagonal de una de las caras del dodecaedro; teniendo todos estos cubos da lugar al compuesto regular de cinco cubos.
Si dos esquinas opuestas de un cubo se truncan a la profundidad de los tres vértices conectados directamente a ellos, se obtiene un octaedro irregular. Ocho de estos octaedros irregular se puede unir a las caras triangulares de un octaedro regular para obtener el cuboctaedro.
El cubo es topológicamente relacionado con una serie de poliedros esféricos y embaldosados con el fin-3 cifras vértice.
| Poliedros | Euclidiana | Teselaciones hiperbólicas | ||||||
|---|---|---|---|---|---|---|---|---|
 {2,3} |  {3,3} |  {4,3} |  {5,3} |  {6,3} |  {7,3} |  {8,3} | ... |  (∞, 3} |
El cuboctaedro es uno de una familia de poliedros uniformes relacionada con el cubo y el octaedro regular.
| Simetría: [4,3], (* 432) | [4,3] +, (432) | [1 +, 4,3], (* 332) | [4,3 +], (3 * 2) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| | | | | | | | | | |
| |  | | |  |  |  |  |  | |
| {4,3} | t 0,1 {4,3} | t 1 {4,3} | t 1,2 {4,3} | {3,4} | t 0,2 {4,3} | t {0,1,2 4,3} | s {4,3} | h {4,3} | h 1,2 {4,3} |
| Gemelos a poliedros uniformes | |||||||||
| | | | | | | | | | |
 |  | | |  |  |  | | |  |
| V4.4.4 | V3.8.8 | V3.4.3.4 | V4.6.6 | V3.3.3.3 | V3.4.4.4 | V4.6.8 | V3.3.3.3.4 | V3.3.3 | V3.3.3.3.3 |
El cubo está relacionada topológicamente como una parte de la secuencia de teselaciones regulares, que se extiende en el plano hiperbólico: {4, p}, p = 3,4,5 ...
 {4,3} |  {4,4} |  {4,5} |  {4,6} |  {4,7} |  {4,8} | ... |  {4, ∞} |
Con simetría diedro, Dih 4, el cubo está relacionada topológicamente en una serie de poliedros uniforme y embaldosados 4.2n.2n, que se extiende en el plano hiperbólico:
| Simetría * N42 [N, 4] | Esférico | Euclidiana | Hiperbólica ... | |||||
|---|---|---|---|---|---|---|---|---|
| * 242 [2,4] 4h D | * 342 [3,4] O h | * 442 [4,4] P4m | * 542 [5,4] | * 642 [6,4] | * 742 [7,4] | * 842 [8,4] ... | * ∞42 [∞, 4] | |
| Truncado cifras |  4.4.4 |  4.6.6 |  4.8.8 |  4.10.10 |  12.04.12 |  04.14.14 |  04.16.16 |  4.∞.∞ |
| Coxeter Schläfli | t 1,2 {4,2} | t 1,2 {4,3} | t 1,2 {4,4} | t 1,2 {4,5} | t 1,2 {4,6} | t 1,2 {4,7} | t 1,2 {4,8} | t 1,2 {4, ∞} |
| Cifras dobles uniformes | ||||||||
| n-kis cifras |  V4.4.4 |  V4.6.6 |  V4.8.8 |  V4.10.10 |  V4.12.12 |  V4.14.14 |  V4.16.16 |  V4.∞.∞ |
| Coxeter | | | | | | | | |
Todas estas cifras tienen simetría octaédrica.
El cubo es una parte de una secuencia de poliedros rómbica y embaldosados con [n, 3] Coxeter simetría grupo. El cubo puede ser visto como un hexaedro rómbica donde los rombos son cuadrados.
| Simetría * N32 [N, 3] | Esférico | Euclidiana | Embaldosado hiperbólico | ||||
|---|---|---|---|---|---|---|---|
| * 332 [3,3] T d | * 432 [4,3] O h | * 532 [5,3] I h | * 632 [6,3] P6M | * 732 [7,3] | * 832 [8,3] | * ∞32 [∞, 3] | |
| Quasiregular cifras configuración |  3.3.3.3 |  3.4.3.4 |  3.5.3.5 |  3.6.3.6 |  3.7.3.7 |  3.8.3.8 |  3.∞.3.∞ |
| Diagrama Coxeter | | | | | | | |
| Dual (Romboidal) cifras configuración |  V3.3.3.3 |  V3.4.3.4 |  V3.5.3.5 |  V3.6.3.6 |  V3.7.3.7 |  V3.8.3.8 |  V3.∞.3.∞ |
| Diagrama Coxeter | | | | | | | |
El cubo es una prisma cuadrado:
| 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ... | ∞ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| | | | | | | | | | | | |
 |  |  |  |  |  | |  |  |  |  | |
| Como poliedros esféricos | |||||||||||
| |  |  | |  |  |  |  | ||||
Como un trapezoedro trigonal, el cubo está relacionado con la familia simetría hexagonal diedro.
| Simetría: [6,2], (* 622) | [6,2] +, (622) | [1 +, 6,2], (322) | [6,2 +], (2 * 3) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| | | | | | | | | | |
| | | |  |  | |  |  |  |  |
| {6,2} | t 0,1 {6,2} | t 1 {6,2} | t 1,2 {6,2} | t 2 {6,2} | t 0,2 {6,2} | t {0,1,2 6,2} | s {6,2} | h {6,2} | h 1,2 {6,2} |
| Duales uniformes | |||||||||
| | | | | | | | | | |
 |  |  |  | |  |  |  |  |  |
| V6 2 | V12 2 | V6 2 | V4.4.6 | V2 6 | V4.4.6 | V4.4.12 | V3.3.3.6 | V3 2 | V3.3.3.3 |
 Compuesto de tres cubos |  Compuesto de cinco cubos |
En panales uniformes y polychora
Es un elemento de 9 de 28 convexa panales uniformes:
También es un elemento de cinco cuatro dimensiones polychora uniforme:
| Tesseract | Cantellated 16 células | Tesseract Runcinated | Cantitruncated 16 células | Runcitruncated 16 células |
 |  |  |  |  |
Cubos combinatorias
Un tipo diferente de cubo es el gráfico de cubo, que es la gráfica de vértices y aristas del cubo geométrico. Se trata de un caso especial de la gráfico hipercubo.
Una extensión es la de tres k -ario dimensional Hamming gráfico, que para k = 2 es el gráfico de cubo. Los gráficos de este tipo se producen en la teoría de la el procesamiento en paralelo en los ordenadores.
- Cubo Unidad
- Tesseract
- Cube (película)
- Trapezohedron
- Yoshimoto Cube
- El Cubo (demostración de juego)
- Cubo de Prince Rupert
- Cubo OLAP
- Cubo Lövheim de emoción
- Cubo de Heymans
- Cubo de Necker
- Cubo de rubik