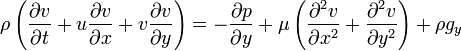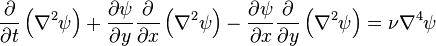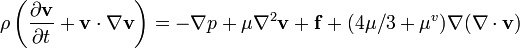Equações de Navier-Stokes
Você sabia ...
Esta seleção wikipedia foi escolhido por voluntários que ajudam Crianças SOS da Wikipedia para este Seleção Wikipedia para as escolas. Visite o site da SOS Children at http://www.soschildren.org/
| Mecânica do contínuo |
|---|
 |
Leis
|
Mecânica dos sólidos
|
|
Reologia
|
As equações de Navier-Stokes, em homenagem Claude-Louis Navier e George Gabriel Stokes, descrever o movimento de substâncias fluidas, tais como líquidos e gases . Essas equações estabelecer que as mudanças na dinâmica de volumes infinitesimais de fluido são simplesmente a soma de dissipação forças viscosas (semelhante ao fricção), mudanças na pressão, gravidade e outras forças agindo dentro do fluido: uma aplicação da segunda lei de Newton para fluido.
Eles são um dos conjuntos mais úteis de equações porque descrevem a física de um grande número de fenômenos de interesse acadêmico e econômico. Eles podem ser utilizados para modelo de tempo , correntes oceânicas, o fluxo de água em uma tubulação, fluem em torno de um aerofólio (asa), e movimento de estrelas dentro de uma galáxia . Como tal, estas equações em ambas as formas completo e simplificado, são utilizados na concepção de aviões e veículos, o estudo da circulação sanguínea, o desenho de centrais eléctricas, a análise dos efeitos da poluição, etc. Em conjunto com as equações de Maxwell puderem ser usado para modelar e estudo magnetohydrodynamics.
As equações de Navier-Stokes também são de grande interesse em um sentido puramente matemático. Surpreendentemente, dada a sua vasta gama de usos práticos, os matemáticos ainda não provaram que em três dimensões soluções sempre existir ( existência), ou que, se eles existem eles não contêm quaisquer infinidades, singularidades ou descontinuidades (suavidade). Estes são chamados a Navier-Stokes existência e suavidade problemas. O Clay Mathematics Institute chamou este um dos sete problemas abertos mais importantes em matemática, e ofereceu um prêmio de US $ 1.000.000 para uma solução ou um contra-exemplo.
As equações de Navier-Stokes são equações diferenciais que, ao contrário equações algébricas, não estabeleça explicitamente uma relação entre as variáveis de interesse (por exemplo, velocidade e pressão). Em vez disso, eles estabelecem relações entre as taxas de variação . Por exemplo, as equações de Navier-Stokes para simples caso de um ideal fluido (não-viscoso) pode-se afirmar que a aceleração (a taxa de variação de velocidade ) é proporcional à gradiente (um tipo de derivado multivariada) de pressão.
Ao contrário do que é normalmente visto em mecânica dos sólidos, as equações de Navier-Stokes não ditar posição, mas em vez da velocidade . A solução das equações de Navier-Stokes é chamado um campo de velocidade de fluxo ou campo, que é uma descrição da velocidade do fluido num dado ponto no tempo e espaço. Uma vez que o campo de velocidade é resolvido para, outras quantidades de interesse (como a taxa de fluxo, força de arrasto, ou o caminho de uma "partícula" de fluido irá tomar) pode ser encontrada.
Propriedades
Não-linearidade
As equações de Navier-Stokes são não-lineares de equações diferenciais parciais em quase todas as situações real (exceções incluem um fluxo dimensional e fluxo rasteira). A não linearidade faz a maioria dos problemas difíceis ou impossíveis de resolver e faz parte da causa turbulência.
A não linearidade é devido a aceleração convectiva, que é uma aceleração associado com a variação da velocidade sobre a posição. Daí, qualquer fluxo convectivo, se turbulento ou não, vai envolver não linearidade, um exemplo de convecção, mas laminar (nonturbulent) fluxo seria a passagem de um fluido viscoso (por exemplo, óleo) através de uma pequena convergente bocal. Esses fluxos, quer sejam exatamente solúvel ou não, muitas vezes pode ser muito bem estudadas e compreendidas.
Turbulência
Turbulência é o tempo dependente caótico comportamento visto em muitos fluxos de fluido. Acredita-se geralmente que é devida à inércia do fluido como um todo: o culminar de tempo de aceleração dependente e convectiva; daí flui onde os efeitos inerciais são pequenos tendem a ser laminar (o Número de Reynolds quantifica a quantidade de fluxo é afectado por inércia). Acredita-se, embora não se sabe com certeza, que as equações de Navier-Stokes modelo de turbulência corretamente.
Mesmo que a turbulência é uma experiência diária, é extremamente difícil encontrar soluções, quantificar, ou em caracterizar geral. A 1000 mil dólares prêmio foi oferecido em Maio de 2000 pela Instituto Clay de Matemática, para quem faz progresso preliminar em direção a uma teoria matemática que vai ajudar na compreensão deste fenômeno.
A solução numérica da Navier-Stokes para fluxo turbulento é extremamente difícil, e devido aos significativamente diferentes escalas de mistura de comprimento que estão envolvidos em fluxo turbulento, a solução estável de este requer uma tal resolução de malha fina que o tempo de processamento torna-se significativamente inviável para o cálculo (ver Simulação numérica direta). As tentativas para resolver o fluxo turbulento laminar utilizando um agente de resolução tipicamente resultar em uma solução de tempo instável, o qual não consegue convergir apropriadamente. Para contrariar esta situação, várias aproximações como a Reynolds em média equações de Navier-Stokes (RANS), complementados com modelos de turbulência (como o modelo k-ε), são utilizados em práticas dinâmica de fluidos computacional (CFD) aplicações na modelagem de escoamentos turbulentos. Outra técnica para resolver numericamente a equação de Navier-Stokes é a simulação de grande redemoinho (LES). Esta abordagem é computacionalmente mais caro do que o método RANS (no tempo e memória do computador), mas produz melhores resultados, uma vez que parte das escalas características turbulentas são explicitamente resolvido.
Aplicabilidade
Juntamente com equações complementares (por exemplo, conservação de massa) e condições de contorno bem formuladas, as equações de Navier-Stokes parecem modelar movimento fluido com precisão; até mesmo fluxos turbulentos parecer (em média) a concordar com as observações do mundo real.
As equações de Navier-Stokes assumir que o fluido a ser estudada é uma continuum. Em escalas muito pequenas ou em condições extremas, fluidos reais feita de moléculas discretas irá produzir resultados diferentes dos fluidos contínuos modelados pelas equações de Navier-Stokes. Dependendo do Número de Knudsen do problema, mecânica estatística ou possivelmente até mesmo dinâmica molecular pode ser uma abordagem mais apropriada.
Outra limitação é muito simplesmente a natureza complicada das equações. Existem formulações testadas em tempo para as famílias de fluidos comuns, mas a aplicação das equações de Navier-Stokes para famílias menos comuns tende a resultar em formulações muito complicadas que são uma área de pesquisa atual. Por esta razão, as equações de Navier-Stokes são geralmente escritos por Fluidos newtonianos.
Derivação e descrição
A derivação das equações de Navier-Stokes começa com a conservação de massa, quantidade de movimento e energia que está sendo escrito para um volume controle arbitrário. Numa sistema de referência inercial, a forma mais geral das equações de Navier-Stokes acaba sendo:
onde 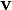 representa a velocidade de fluxo,
representa a velocidade de fluxo,  é a densidade do fluido, p é a pressão,
é a densidade do fluido, p é a pressão,  é o ( deviatoric) estresse tensor, e
é o ( deviatoric) estresse tensor, e  representa forças de corpo (por unidade de volume) que actuam sobre o fluido e
representa forças de corpo (por unidade de volume) que actuam sobre o fluido e  é o operador del. Esta é uma afirmação da conservação da quantidade de movimento em um fluido e é uma aplicação da segunda lei de Newton para um continuum. Esta equação é frequentemente escritos utilizando o substantivo derivado, tornando-se mais evidente que esta é uma afirmação da lei de Newton:
é o operador del. Esta é uma afirmação da conservação da quantidade de movimento em um fluido e é uma aplicação da segunda lei de Newton para um continuum. Esta equação é frequentemente escritos utilizando o substantivo derivado, tornando-se mais evidente que esta é uma afirmação da lei de Newton:
O lado esquerdo da equação descreve aceleração, e pode ser composta de tempo efeitos dependentes ou convectivos (também os efeitos de coordenadas não-inerciais se presente). O lado direito da equação é na verdade um somatório de forças do corpo (como a gravidade) e derivados espaciais de forças de superfície (pressão e estresse).
Aceleração convectiva

Uma característica muito importante das equações de Navier-Stokes é a presença de aceleração convectiva. Estes termos descrevem a aceleração do tempo independente de um fluido em relação ao espaço, e são representados pela quantidade:
O gradiente do vetor velocidade seria mais corretamente ser escrito com a derivado como tensor  , Onde
, Onde  é o Matriz Jacobiana da velocidade em relação ao espaço. Existem algumas outras formas de representar convecção:
é o Matriz Jacobiana da velocidade em relação ao espaço. Existem algumas outras formas de representar convecção:
A segunda forma acima usa a operador de advecção e é comum (note a diferença entre advecção e convecção - advecção refere-se especificamente ao transporte de um escalar). A terceira forma foi utilizar no fluxo irrotacional, onde o onda da velocidade (chamado vorticidade) 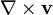 está ausente.
está ausente.
Independentemente do tipo de fluido está sendo tratado, aceleração convectiva é um efeito não linear. Convecção está presente na maioria dos fluxos, as exceções incluem rastejando fluxo e escoamento incompressível em uma dimensão.
Salienta
Tensão em que o fluido é representado pela  e
e 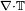 termos, estes são gradientes de forças de superfície, análogas às tensões na forma de um sólido.
termos, estes são gradientes de forças de superfície, análogas às tensões na forma de um sólido.  é chamada de gradiente de pressão e surge a partir tensões normais que aparecem em quase todas as situações, dinâmicos ou não.
é chamada de gradiente de pressão e surge a partir tensões normais que aparecem em quase todas as situações, dinâmicos ou não. 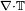 convencionalmente descreve forças viscosas; para escoamento incompressível, este é apenas um efeito de corte.
convencionalmente descreve forças viscosas; para escoamento incompressível, este é apenas um efeito de corte.
Interessantemente, apenas o gradiente de pressão mostra-se, e não a própria pressão. O efeito do gradiente de pressão é que o fluido flua a partir de alta pressão à baixa pressão.
O termo estresse 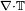 contém muitas incógnitas para ser imediatamente utilizável, daí a forma geral acima não é directamente aplicável a problemas práticos. Por esta razão, as suposições sobre o comportamento viscoso específica de um fluido são feitas (com base em observações naturais) e aplicadas, a fim de especificar essa quantidade em termos de variáveis conhecidas, tais como a velocidade. Por exemplo, o termo torna-se a quantidade útil
contém muitas incógnitas para ser imediatamente utilizável, daí a forma geral acima não é directamente aplicável a problemas práticos. Por esta razão, as suposições sobre o comportamento viscoso específica de um fluido são feitas (com base em observações naturais) e aplicadas, a fim de especificar essa quantidade em termos de variáveis conhecidas, tais como a velocidade. Por exemplo, o termo torna-se a quantidade útil 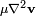 quando o fluido incompressível e é assumido Newtoniana.
quando o fluido incompressível e é assumido Newtoniana.
Outras forças
 representa "outro" ( força corporal) forças. Tipicamente esta é apenas gravidade , mas podem incluir outros campos (tais como electromagnética). Em um não-inercial sistema de coordenadas, outras "forças", como o que se relaciona com coordenadas de rotação pode ser inserido.
representa "outro" ( força corporal) forças. Tipicamente esta é apenas gravidade , mas podem incluir outros campos (tais como electromagnética). Em um não-inercial sistema de coordenadas, outras "forças", como o que se relaciona com coordenadas de rotação pode ser inserido.
Muitas vezes, estas forças podem ser representados como o gradiente de alguma quantidade escalar. A gravidade da  direcção, por exemplo, é o gradiente de
direcção, por exemplo, é o gradiente de  . Uma vez que a pressão mostra-se apenas como um gradiente, isto implica que a solução de um problema sem qualquer força de corpo pode ser reparado a incluir a força do corpo através da modificação da pressão.
. Uma vez que a pressão mostra-se apenas como um gradiente, isto implica que a solução de um problema sem qualquer força de corpo pode ser reparado a incluir a força do corpo através da modificação da pressão.
Outras equações
As equações de Navier-Stokes são estritamente uma declaração da conservação do momento. A fim de descrever completamente o fluxo de fluido, são necessárias mais informações (quanto depende das suposições feitas), o que pode incluir dados de limite ( não-slip, superfície capilar, etc), a conservação da massa, a conservação de energia, e / ou uma equação de estado.
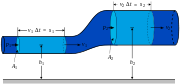
Independentemente das premissas de fluxos, uma declaração do conservação da massa é geralmente necessário. Isto é conseguido através da massa equação de continuidade, tendo em conta na sua forma mais geral, como:
ou, usando o derivado de fundo:
Escoamento incompressível de fluidos newtonianos
A grande maioria dos trabalhos sobre as equações de Navier-Stokes é feito sob um premissa de fluxo incompressível para Fluidos newtonianos. A premissa de fluxo incompressível normalmente tem bem, mesmo quando se trata de um fluido "compressível", tal como o ar à temperatura ambiente (mesmo quando flui até cerca de Mach 0,3). Tomando a suposição de escoamento incompressível em conta e assumindo viscosidade constante, as equações de Navier-Stokes vai ler (na forma vetorial):
f representa "outro" forças de corpo (forças por unidade de volume), tais como a gravidade ou força centrífuga. Vale a pena observar o significado de cada termo:
Note que apenas os termos convectivos são não-lineares para o fluxo incompressível newtoniana. A aceleração convectiva é uma aceleração causada por uma alteração (possivelmente estável) na velocidade sobre a posição, por exemplo, a aceleração do fluido entrar numa convergente bocal. Embora as partículas de fluido individuais estão a ser aceleradas e, portanto, estão no âmbito movimento instável, o campo de fluxo (uma distribuição de velocidade) não será, necessariamente, dependente do tempo.
Outra observação importante é a de que a viscosidade é representado pela Laplaciano vector do campo de velocidades. Isto implica que a viscosidade Newtoniana é a difusão de impulso, esta funciona da mesma maneira como o difusão de calor visto na equação do calor (que também envolve o Laplaciano).
Se os efeitos da temperatura também são negligenciadas, a única equação "outro" (além de condições iniciais / limite) necessário é a equação de continuidade de massa. Sob a hipótese de incompressível, a densidade é uma constante e segue-se que a equação irá simplificar a:
Este é mais especificamente uma declaração da conservação das unidades (ver divergência).
Estas equações são normalmente utilizados em sistemas de coordenadas 3: Cartesiano, cilíndrico, e esférica . As equações cartesianas siga diretamente a partir da equação do vetor acima, a obtenção de equações em outros sistemas de coordenadas exigirá um mudança de variáveis.
Coordenadas cartesianas
Escrevendo a equação vetorial de forma explícita,
Note-se que a gravidade foi contabilizada como uma força do corpo, e os valores de  dependerá da orientação da gravidade em relação ao conjunto escolhido de coordenadas.
dependerá da orientação da gravidade em relação ao conjunto escolhido de coordenadas.
A equação de continuidade lê:
Note-se que os componentes da velocidade (as variáveis dependentes para ser resolvido para) são  ,
,  ,
, 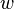 . Este sistema de quatro equações compreende a forma mais vulgarmente utilizada e estudada. Embora comparativamente mais compacto do que outras representações, este é um sistema não-linear de equações diferenciais parciais para os quais soluções são difíceis de obter.
. Este sistema de quatro equações compreende a forma mais vulgarmente utilizada e estudada. Embora comparativamente mais compacto do que outras representações, este é um sistema não-linear de equações diferenciais parciais para os quais soluções são difíceis de obter.
Coordenadas cilíndricas
A mudança de variáveis nas equações cartesianas trará as seguintes equações de momentum para r, θ, e z:
Os componentes de gravidade em geral, não serão constantes, no entanto, para a maioria das aplicações, quer as coordenadas são escolhidos de modo que os componentes de gravidade são constantes, ou então presume-se que a gravidade é contrariado por um campo de pressão (por exemplo, o fluxo no tubo horizontal é tratado normalmente, sem gravidade e sem um gradiente de pressão vertical). A equação da continuidade é:
Esta representação cilíndrica dos incompressíveis equações de Navier-Stokes é a segunda mais comumente visto (a primeira foi cartesiano acima). Coordenadas cilíndricas são escolhidos para tirar proveito de simetria, de modo que uma componente da velocidade pode desaparecer. Um caso muito comum é o fluxo de simetria axial, em que não há nenhuma velocidade tangencial (  ) E as quantidades restantes são independentes
) E as quantidades restantes são independentes  :
:
Coordenadas esféricas
Em coordenadas esféricas , o  ,
,  E
E  equações de momentum são (note a convenção usada:
equações de momentum são (note a convenção usada:  é colatitude):
é colatitude):
Continuidade massa vai ler:
Estas equações podem ser (ligeiramente) simplificada, por exemplo, o factoring 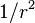 dos termos viscosos. Isto não é feito para preservar a estrutura do Laplaciano e outras quantidades.
dos termos viscosos. Isto não é feito para preservar a estrutura do Laplaciano e outras quantidades.
Formulação função corrente
Tomando o curvatura dos resultados da equação de Navier-Stokes na eliminação da pressão. Isto é especialmente fácil de ver se o fluxo cartesiano 2D é assumido ( 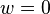 e sem dependência de qualquer coisa em
e sem dependência de qualquer coisa em  ), Em que as equações reduzir a:
), Em que as equações reduzir a:
Diferenciando a primeira diz respeito a  , A segunda no que diz respeito aos
, A segunda no que diz respeito aos  e subtraindo as equações resultantes irá eliminar qualquer pressão e força potencial. Definindo o função de corrente
e subtraindo as equações resultantes irá eliminar qualquer pressão e força potencial. Definindo o função de corrente  através
através
resultados em continuidade massa estar satisfeito incondicionalmente (dada a função de corrente é contínua), e, em seguida, incompressível dinâmica newtoniana 2D e conservação de massa degradar em uma equação:
onde  é o (2D) operador operador biharmônico e
é o (2D) operador operador biharmônico e 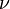 é o do viscosidade cinemática. Esta única equação juntamente com condições de contorno apropriadas descreve o fluxo de fluido 2D, tendo viscosidade cinemática única como um parâmetro. Note-se que a equação rastejando resultados de fluxo quando o lado esquerdo é assumido zero.
é o do viscosidade cinemática. Esta única equação juntamente com condições de contorno apropriadas descreve o fluxo de fluido 2D, tendo viscosidade cinemática única como um parâmetro. Note-se que a equação rastejando resultados de fluxo quando o lado esquerdo é assumido zero.
Fluxo compressível de fluidos newtonianos
Existem alguns fenômenos excepcionais que estão intimamente ligados com fluido compressibilidade. Um dos exemplos é óbvio som . Descrição de tais fenômenos exige apresentação mais geral da equação de Navier-Stokes, que leva em conta a compressibilidade do fluido. Se a viscosidade é assumida uma constante, um prazo adicional aparece, como mostrado aqui:
μ onde v é o segundo coeficiente de viscosidade. Ela está relacionada com volume de viscosidade ou viscosidade a granel. Este prazo adicional desaparece para fluido incompressível, quando o divergência do fluxo é igual a 0.
Aplicativo para problemas específicos
As equações de Navier-Stokes, mesmo quando escritos explicitamente para fluidos específicos, são bastante genérico na natureza e na sua aplicação adequada para problemas específicos podem ser muito diversas. Isto é em parte porque existe uma enorme variedade de problemas que podem ser modelados, variando de tão simples como a distribuição de pressão estática para tão complicado como o fluxo multifásico impulsionado pela tensão superficial .
Geralmente, a aplicação de problemas específicos começa com algumas hipóteses de fluxo e formulação condição inicial / limite, isto pode ser seguido pela análise de escala para simplificar ainda mais o problema. Por exemplo, depois de assumir constante, em paralelo, de uma dimensão, a pressão nonconvective conduzido fluxo entre as placas paralelas, a resultante dimensionado (adimensional) problema do valor limite é:

A condição de contorno é o nenhuma condição de deslizamento. Este problema é resolvido facilmente para o campo de fluxo:
Deste ponto em diante mais quantidades de interesse pode ser facilmente obtida, como força de arrasto viscoso ou taxa de fluxo líquido.
Podem surgir dificuldades quando o problema se torna um pouco mais complicado. Uma torção aparentemente modesta sobre o fluxo paralelo acima seria o fluxo radial entre as placas paralelas; isso envolve a convecção e deste modo não-linearidade. O campo de velocidades pode ser representada por uma função 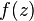 que devem satisfazer:
que devem satisfazer:
Esta equação diferencial ordinária é o que é obtido quando as equações de Navier-Stokes são escritos e os pressupostos de fluxo aplicadas (adicionalmente, o gradiente de pressão é resolvido para). O não-linear prazo torna este um problema muito difícil de resolver analiticamente (uma longa podem ser encontrado solução implícito que envolve integrais elípticas e raízes de polinômios cúbicos). Problemas com a existência real de soluções surgem para R> 22,609 (aproximadamente), o parâmetro R sendo o Número de Reynolds com escalas adequadamente escolhidos. Este é um exemplo de premissas de fluxos de perder sua aplicabilidade, e um exemplo da dificuldade em "alta" com números de Reynolds.

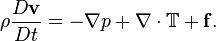


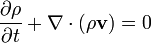

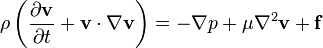
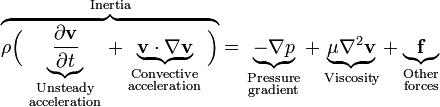
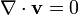
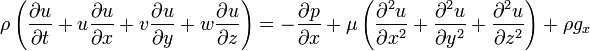

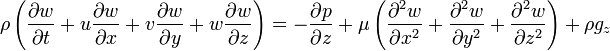

![\ Rho \ left (\ frac {\ u_r parcial} {\ t parcial} + u_r \ frac {\ u_r parcial} {\ r parcial} + \ frac {u _ {\ theta}} {r} \ frac {\ u_r parcial } {\ \ theta parcial} + u_z \ frac {\ u_r parcial} {\ z parcial} - \ frac {u _ {\ theta} ^ 2} {R} \ right) = - \ frac {\ p parcial} {\ r parcial} + \ mu \ left [\ frac {1} {R} \ frac {\ partial} {\ r parcial} \ left (r \ frac {\ u_r parcial} {\ r parcial} \ right) + \ frac {1} {r ^ 2} \ frac {\ partial ^ 2 u_r} {\ \ theta parcial ^ 2} + \ frac {\ partial ^ 2 u_r} {\ z parcial ^ 2} - \ frac {} {r u_r ^ 2} - \ frac {2} {r ^ 2} \ frac {\ u _ {\ theta}} {parcial \ \ theta parcial} \ right] + \ g_r rho](../../images/181/18167.png)
![\ Rho \ left (\ frac {\ u _ {\ theta} parcial} {\ t parcial} + u_r \ frac {\ partial u _ {\ theta}} {\ r parcial} + \ frac {u _ {\ theta}} { r} \ frac {\ partial u _ {\ theta}} {\ \ theta parcial} + u_z \ frac {\ partial u _ {\ theta}} {\ z parcial} + \ frac {u_r u _ {\ theta}} {r } \ right) = - \ frac {1} {R} \ frac {\ p parcial} {\ \ theta} parcial + \ mu \ left [\ frac {1} {R} \ frac {\ partial} {\ partial r} \ left (r \ frac {\ partial u _ {\ theta}} {\ r parcial} \ right) + \ frac {1} {r ^ 2} \ frac {\ partial ^ 2 u _ {\ theta}} { \ \ theta parcial ^ 2} + \ frac {\ partial ^ 2 u _ {\ theta}} {\ partial z ^ 2} + \ frac {2} {r ^ 2} \ frac {\ u_r parcial} {\ partial \ theta} - \ frac {u _ {\ theta}} {r ^ 2} \ right] + \ rho g _ {\ theta}](../../images/181/18168.png)
![\ Rho \ left (\ frac {\ u_z parcial} {\ t parcial} + u_r \ frac {\ u_z parcial} {\ r parcial} + \ frac {u _ {\ theta}} {r} \ frac {\ u_z parcial } {\ \ theta} parcial + u_z \ frac {\ u_z parcial} {\ z parcial} \ right) = - \ frac {\ p parcial} {\ z parcial} + \ mu \ left [\ frac {1} { r} \ frac {\ partial} {\ r parcial} \ left (r \ frac {\ u_z parcial} {\ r parcial} \ right) + \ frac {1} {r ^ 2} \ frac {\ partial ^ 2 u_z} {\ \ theta parcial ^ 2} + \ frac {\ partial ^ 2 u_z} {\ z parcial ^ 2} \ right] + \ g_z rho](../../images/181/18169.png)

![\ Rho \ left (\ frac {\ u_r parcial} {\ t parcial} + u_r \ frac {\ u_r parcial} {\ r parcial} + u_z \ frac {\ u_r parcial} {\ z parcial} \ right) = - \ frac {\ p parcial} {\ r parcial} + \ mu \ left [\ frac {1} {R} \ frac {\ partial} {\ r parcial} \ left (r \ frac {\ u_r parcial} {\ r parcial} \ right) + \ frac {\ partial ^ 2 u_r} {\ z ^ 2} parcial - \ frac {u_r} {r ^ 2} \ right] + \ g_r rho](../../images/181/18172.png)
![\ Rho \ left (\ frac {\ u_z parcial} {\ t parcial} + u_r \ frac {\ u_z parcial} {\ r parcial} + u_z \ frac {\ u_z parcial} {\ z parcial} \ right) = - \ frac {\ p parcial} {\ z parcial} + \ mu \ left [\ frac {1} {R} \ frac {\ partial} {\ r parcial} \ left (r \ frac {\ u_z parcial} {\ r parcial} \ right) + \ frac {\ partial ^ 2 u_z} {\ z parcial ^ 2} \ right] + \ g_z rho](../../images/181/18173.png)


![\ Mu \ left [\ frac {1} {r ^ 2} \ frac {\ partial} {\ r parcial} \ left (r ^ 2 \ frac {\ u_r parcial} {\ r parcial} \ right) + \ frac {1} {r ^ 2 \ sin (\ phi) ^ 2} \ frac {\ partial ^ 2 u_r} {\ \ theta parcial ^ 2} + \ frac {1} {r ^ 2 \ sin (\ phi)} \ frac {\ partial} {\ \ phi parcial} \ left (\ sin (\ phi) \ frac {\ u_r parcial} {\ \ phi parcial} \ right) - 2 \ frac {u_r + \ frac {\ u_ parcial {\ phi}} {\ \ phi parcial} + u _ {\ phi} \ berço (\ phi)} {r ^ 2} + \ frac {2} {r ^ 2 \ sin (\ phi)} \ frac {\ parcial u _ {\ theta}} {\ partial \ theta} \ right]](../../images/181/18176.png)

![\ Mu \ left [\ frac {1} {r ^ 2} \ frac {\ partial} {\ r parcial} \ left (r ^ 2 \ frac {\ u _ {\ theta} parcial} {\ r parcial} \ right ) + \ frac {1} {r ^ 2 \ sin (\ phi) ^ 2} \ frac {\ partial ^ 2 u _ {\ theta}} {\ \ theta parcial ^ 2} + \ frac {1} {r ^ 2 \ sin (\ phi)} \ frac {\ partial} {\ \ phi parcial} \ left (\ sin (\ phi) \ frac {\ partial u _ {\ theta}} {\ \ phi parcial} \ right) + \ frac {2 \ frac {\ u_r parcial} {\ \ theta parcial} + 2 \ cos (\ phi) \ frac {\ partial u _ {\ theta}} {\ \ theta parcial} - u _ {\ theta}} { r ^ 2 \ sin (\ phi) ^ 2} \ right]](../../images/181/18178.png)

![\ Mu \ left [\ frac {1} {r ^ 2} \ frac {\ partial} {\ r parcial} \ left (r ^ 2 \ frac {\ u _ {\ phi} parcial} {\ r parcial} \ right ) + \ frac {1} {r ^ 2 \ sin (\ phi) ^ 2} \ frac {\ partial ^ 2 u _ {\ phi}} {\ \ theta parcial ^ 2} + \ frac {1} {r ^ 2 \ sin (\ phi)} \ frac {\ partial} {\ \ phi parcial} \ left (\ sin (\ phi) \ frac {\ partial u _ {\ phi}} {\ \ phi parcial} \ right) + \ frac {2} {r ^ 2} \ frac {\ u_r parcial} {\ \ parcial phi} - \ frac {u _ {\ phi} + 2 \ cos (\ phi) \ frac {\ partial u _ {\ theta} } {\ \ theta}} {parcial r ^ 2 \ sin (\ phi) ^ 2} \ right]](../../images/181/18180.png)