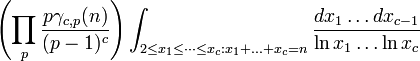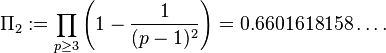Conjecture de Goldbach

À propos de ce écoles sélection Wikipedia

Cette sélection se fait pour les écoles par la charité pour enfants lire la suite . Voulez-vous savoir sur le parrainage? Voir www.sponsorachild.org.uk

Conjecture de Goldbach est une des plus anciennes problèmes non résolus dans la théorie des nombres et dans toutes les mathématiques . Il déclare:

Chaque même nombre entier supérieur à 2 peut être écrite comme la somme de deux nombres premiers .

Exprimant un même nombre déterminé comme une somme de deux nombres premiers est appelé un Goldbach le nombre de partition. Par exemple,

4 = 2 + 2

6 + 3 = 3

8 = 3 + 5

10 = 3 + 7 = 5 + 5

12 = 5 + 7

14 + 3 = 11 = 7 + 7

...

En d'autres termes, la conjecture de Goldbach indique que chaque nombre pair supérieur ou égal à quatre est un nombre Goldbach, un nombre qui peut être exprimée comme la somme de deux nombres premiers. Voir également La conjecture de Levy.

Une illustration de la conjecture de Goldbach.

Origines

Sur 7 Juin 1742, le Prussienne mathématicien Christian Goldbach a écrit une lettre à Leonhard Euler (lettre XLIII) dans lequel il proposait la conjecture suivante:

Chaque nombre entier supérieur à deux peut être écrite comme la somme de trois nombres premiers.

Il a considéré 1 à un nombre premier , une convention ensuite abandonnées. Une version moderne de la conjecture de Goldbach est originale:

Chaque nombre entier supérieur à 5 peut être écrite comme la somme de trois nombres premiers.

Euler, de se intéresser à ce problème, a répondu en faisant remarquer que cette conjecture est équivalente avec une autre version:

Chaque entier pair supérieur à 2 peut être écrit comme la somme de deux nombres premiers,

ajoutant qu'il considérait cette un tout à fait certain théorème ("ein ganz gewisses Theorema"), en dépit de son incapacité à prouver.

La version d'Euler est la forme sous laquelle la conjecture est habituellement exprimée aujourd'hui. Il est également connu comme le " forte "," même "ou" binaire "conjecture de Goldbach, pour le distinguer d'un corollaire plus faible. La conjecture de Goldbach forte implique la conjecture que tous les numéros impairs supérieurs 7 sont la somme de trois nombres premiers impairs, qui est connu aujourd'hui diversement comme la "Faible" conjecture de Goldbach, le "bizarre" conjecture de Goldbach, ou "ternaire" conjecture de Goldbach. Ces deux questions sont restées en suspens depuis, bien que la forme faible de la conjecture semble être beaucoup plus proche de la résolution que le fort. Si la conjecture de Goldbach forte est vrai, la faiblesse de la conjecture de Goldbach sera vrai implicitement.

Résultats vérifiés

Pour les petites valeurs de n, la conjecture de Goldbach forte (et donc la faiblesse de la conjecture de Goldbach) peuvent être vérifiées directement. Par exemple, en 1938 N. Pipping vérifiée laborieusement la conjecture jusqu'à 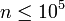$n \ leq 10 ^ 5$ . Avec l'avènement des ordinateurs, beaucoup plus petites valeurs de n ont été vérifiées; T. 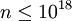Oliveira e Silva se exécute une recherche informatique distribué qui a vérifié la conjecture pour $n \ leq 10 ^ {18}$ .

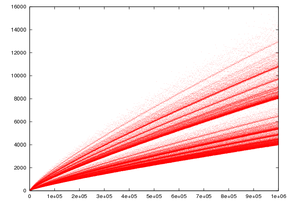
La conjecture de Goldbach ne dit pas qu'un certain nombre doit être la somme d'une paire unique de nombres premiers. Les exemples de cet article illustrent le fait que plus d'une paire de nombres premiers peut totaliser le même nombre.

Justification heuristique

Considérations statistiques qui mettent l'accent sur la distribution probabiliste des nombres premiers de présenter des preuves informelle en faveur de la conjecture (dans les deux formes les faibles et forts) pour suffisamment grands entiers: plus le nombre entier, les plus de moyens sont disponibles, pour ce nombre à être représenté comme la somme de deux ou trois autres numéros, et plus «probable», il devient qu'au moins une de ces représentations est entièrement constitué de nombres premiers .

Nombre de voies d'écrire un nombre pair n comme la somme de deux nombres premiers (4 ≤ n ≤ 1000)

Nombre de voies d'écrire un nombre pair n comme la somme de deux nombres premiers (4 ≤ n ≤ 1000000)

Une version très grossière de la l'argument probabiliste heuristique (pour la forme forte de la conjecture de Goldbach) est la suivante. Le théorème des nombres premiers affirme qu'un m entier choisi au hasard a environ un $1 / \ ln m \, \!$ chance d'être premier. Ainsi, si n est un grand entier pair et m est un nombre compris entre 3 et n / 2, alors on pourrait se attendre à la probabilité de m et nm étant simultanément Premier être $1 \ big / \ big [\ ln m \, \ ln (n-m) \ big]$ . Cette heuristique est pas rigoureuse pour un certain nombre de raisons; par exemple, il suppose que les événements qui m et $n-m$ sont premiers sont statistiquement indépendants les uns des autres. Néanmoins, si l'on poursuit cette heuristique, on pourrait se attendre le nombre total de façons d'écrire un grand n entier pair comme la somme de deux nombres premiers impairs soit environ

$\ Sum_ {m = 3} ^ {n / 2} \ frac {1} {\ ln m} {1 \ over \ ln (nm)} \ approx \ frac {n} {2 \ ln ^ 2 n}.$

Depuis cette quantité tend vers l'infini lorsque n augmente, nous attendre à ce que toutes les grandes entier pair a pas seulement une représentation comme la somme de deux nombres premiers, mais en fait a très grand nombre de ces représentations.

L'argument heuristique ci-dessus est en fait quelque peu imprécis, car il ignore une certaine dépendance entre les événements de m et $n-m$ être premier. Par exemple, si m est impair, alors $n-m$ est également bizarre, et si m est pair, alors $n-m$ est même, une relation non-trivial parce que (plus 2) seulement des nombres impairs peut être privilégié. De même, si n est divisible par 3, et m est déjà un premier distinct de 3, puis $n-m$ serait également premiers entre eux à 3 et donc être légèrement plus susceptibles d'être premier d'un numéro général. Poursuivant ce type d'analyse plus attentivement, Hardy et Littlewood en 1923 conjecturé (dans le cadre de leur célèbre Hardy-Littlewood tuple Premier conjecture) que pour tout fixe c ≥ 2, le nombre de représentations d'un grand entier n que la somme des nombres premiers c $n = p_1 + \ dotsb + P_c$ avec $p_1 \ leq \ dotsb \ leq P_c$ devrait être asymptotiquement égal à

$\ Left (\ prod_p \ frac {p \ gamma_ {c, p} (n)} {(p-1) ^ c} \ right) \ INT_ {2 \ leq x_1 \ leq \ dotsb \ leq x_c: x_1 + \ ldots + x_c = n} \ frac {dx_1 \ ldots dx_ {c-1}} {\ ln x_1 \ ldots \ ln x_c}$

où le produit est sur tous les nombres premiers p et 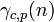$\ {C gamma_, p} (n)$ est le nombre de solutions de l'équation $n = q_1 + \ ldots + q_c \ mod p$ en arithmétique modulaire , sous réserve que contraintes $q_1, \ ldots, q_c \ neq 0 \ mod p$ . Cette formule a été rigoureusement avéré être asymptotiquement valable pour c ≥ 3 des travaux de Vinogradov, mais est encore qu'une conjecture quand $c = 2$ . 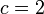Dans ce dernier cas, la formule ci-dessus se simplifie à 0 lorsque n est impair, et à

$2 \ Pi_2 \ left (\ prod_ {p | n; p \ geq 3} \ frac {p-1} {2} p-\ right) \ int_2 ^ n \ frac {dx} {\ ln ^ 2 x} \ environ 2 \ Pi_2 \ left (\ prod_ {p | n; p \ geq 3} \ frac {p-1} {2} p-\ right) \ frac {n} {\ ln ^ 2 n}$

lorsque n est pair, où $\ Pi_2$ est le constante premiers jumeaux

$\ Pi_2: = \ prod_ {p \ geq 3} \ left (1 - \ frac {1} {(p-1) ^ 2} \ right) = 0,6601618158 \ ldots.$

Cette asymptotique est parfois connu comme la conjecture de Goldbach étendu. La conjecture de Goldbach forte est en fait très similaire à la conjecture des nombres premiers jumeaux, et les deux conjectures sont soupçonnés d'être des difficultés à peu près comparable.

Les fonctions de partition présentées ici peuvent être affichés sous forme d'histogrammes qui illustrent informative les équations ci-dessus. Voir La comète de Goldbach.

Résultats rigoureux

Le faible conjecture de Goldbach est assez proche de la résolution.

La conjecture de Goldbach forte est beaucoup plus difficile. Le travail de Vinogradov en 1937 et Theodor Estermann (1902-1991) en 1938 a montré que la quasi-totalité des numéros pairs peuvent se écrire comme la somme de deux nombres premiers (en ce sens que la fraction de nombres pairs qui peuvent être écrites de manière tend vers 1). En 1930, Lev Schnirelmann prouvé que chaque nombre pair n ≥ 4 peuvent être écrits comme la somme d'au plus 300 000 premiers. Ce résultat a été améliorée par la suite par de nombreux auteurs; actuellement, le résultat le plus connu est dû à Olivier Ramaré, qui, en 1995 ont montré que chaque nombre pair n ≥ 4 est en fait la somme d'au plus six premiers. En fait, la résolution de la conjecture de Goldbach faible impliquera aussi directement que chaque nombre pair n ≥ 4 est la somme d'au plus quatre premiers.

Chen Jingrun montré en 1973 en utilisant les procédés de théorie que chaque tamis même nombre suffisamment grand peut être écrite comme une somme de deux nombres premiers soit, ou un premier et un Nombre semi-premier (le produit de deux nombres premiers) -eg, 100 = 23 + 7 · 11.

En 1975, Hugh Montgomery et Robert Charles Vaughan a montré que «la plupart» des nombres pairs étaient exprimable comme la somme de deux nombres premiers. Plus précisément, ils ont montré qu'il existait des constantes positives 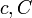$c, C$ telle que pour tout nombre N suffisamment grand, chaque nombre pair inférieur à N est la somme de deux nombres premiers, avec au plus $C N ^ {1-c}$ exceptions. En particulier, l'ensemble des entiers qui ne sont pas même la somme de deux nombres premiers a une densité zéro.

Roger Heath-Brown et Jan-Christoph Schlage-Puchta a montré en 2002 que chaque entier pair assez grand est une somme de deux nombres premiers et exactement 13 puissances de 2.

On peut poser des questions similaires quand les amorces sont remplacés par d'autres ensembles de nombres spéciaux, tels que les carrés. Par exemple, il était prouvée par Lagrange que chaque nombre entier positif est la somme de quatre carrés. Voir Le problème de Waring.

Tentatives preuves

Comme avec beaucoup de conjectures célèbres en mathématiques, il ya un certain nombre de preuves de prétendues la conjecture de Goldbach, dont aucune ne est actuellement acceptée par la communauté mathématique.

Parce que ce est facile à comprendre par des laïcs, la conjecture de Goldbach est une cible populaire pour les mathématiciens amateurs, qui tentent souvent de prouver ou de réfuter en utilisant seulement les mathématiques de niveau lycée. Il partage ce sort avec le théorème des quatre couleurs et le dernier théorème de Fermat , qui ont tous deux également un problème facilement déclaré mais semble néanmoins être résolues que par des méthodes extrêmement élaborés.

Dans la culture populaire

Pour générer de la publicité pour le livre Oncle Petros et la conjecture de Goldbach par Apostolos Doxiadis, éditeur britannique Tony Faber a offert un prix $ 1.000.000 pour une preuve de la conjecture en 2000, si la preuve a été présentée avant Avril 2002. Le prix n'a jamais été réclamé.
Le drame de télévision Lewis a présenté un professeur de mathématiques à l'Université d'Oxford qui avait remporté le Médaille Fields pour ses travaux sur la conjecture de Goldbach, qui était une caractéristique principale de la parcelle.
Courte histoire d'Isaac Asimov "Sixty Million Trillion Combinaisons" présentait un mathématicien qui soupçonne que son travail sur la conjecture de Goldbach avait été volé.
Dans le Film espagnol "La habitación de Fermat" (2007), réalisé par Luis Piedrahita et Rodrigo Sopeña, un jeune mathématicien affirme avoir résolu le Conjecture.

Récupéré à partir de " http://en.wikipedia.org/w/index.php?title=Goldbach%27s_conjecture&oldid=208155239 "